SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Number, NAPX-p107088v02 SA

The product of three different positive whole numbers is 48.

What is the smallest possible sum of the three different numbers?

 

Show Answers Only

`12`

Show Worked Solution
`48` `= 24 xx 2 xx 1,\ text(sum = 27)`
`48` `= 12 xx 4 xx 1,\ text(sum = 17)`
  `vdots`
`48` `=8 xx 3 xx 2,\ text(sum = 13)`
`48` `=6 xx 4 xx 2,\ text(sum = 12)`

 
`:.\ text(The smallest possible sum is 12, made up of 6, 4 and 2.)`

Number, NAPX-p107088v01 SA

The product of three different positive whole numbers is 60.

What is smallest possible sum of the three different numbers?

 

Show Answers Only

`12`

Show Worked Solution

`text(Testing some possible combinations:)`

`60` `= 30 xx 2 xx 1,\ text(sum = 33)`
`60` `= 10 xx 3 xx 2,\ text(sum = 15)`
  `vdots`
`60` `= 6 xx 5 xx 2,\ text(sum = 13)`
`60` `=5 xx 4 xx 3,\ text(sum = 12)`

 

`:.\ text(The smallest possible numbers are 5, 4 and 3, with a sum of 12.)`

Number, NAPX-p115611v04 SA

A 5-cent coin has a mass of 3.1 grams.

A 20-cent coin has a mass of 5.3 grams.

Jonathan has 198.4 grams of 5-cent coins.

Kevin has 964.6 grams of 20-cent coins.

How much more worth of coins does Kevin have than Jonathan, in cents?

$  

Show Answers Only

`$33.20`

Show Worked Solution
`text(Jonathan’s total)` `= text(Total mass of coins)/text(mass of 1 coin) xx text(5 cents)`
  `= 198.4/3.1 xx 5`
  `= 64 xx 5`
  `= 320\ text(cents)`

 

`text(Kevin’s total)` `= text(Total mass of coins)/text(mass of 1 coin) xx text(20 cents)`
  `= 964.6/5.3 xx 20`
  `= 182 xx 20`
  `= 3640\ text(cents)`

 

`:.\ text(Difference)` `= 3640 – 320`
  `= 3320\ text(cents)`
  `=$33.20`

Number, NAPX-p115611v03 SA

A 10-cent coin has a mass of 6.2 grams.

A 5-cent coin has a mass of 2.9 grams.

Rico has 347.2 grams of 10-cent coins.

Jester has 301.6 grams of 5-cent coins.

How much more worth of coins does Rico have than Jester, in cents?

 

Show Answers Only

`text(40 cents)`

Show Worked Solution
`text(Rico’s total)` `= text(Total mass of coins)/text(mass of 1 coin) xx 10\ text(cents)`
  `= 347.2/6.2 xx 10`
  `= 56 xx 10`
  `= 560\ text(cents)`

 

`text(Jester’s total)` `= text(Total mass of coins)/text(mass of 1 coin) xx text(5 cents)`
  `= 301.6/2.9 xx 5`
  `= 104 xx 5`
  `= 520\ text(cents)`

 

`:.\ text(Difference)` `= 560 – 520`
  `= 40\ text(cents)`

Number, NAPX-p115611v02 SA

A 50-cent coin has a mass of 14.65 grams.

A 20-cent coin has a mass of 12.1 grams.

Karen has 307.65 grams of 50-cent coins.

Shyla has 508.2 grams of 20-cent coins.

How much more worth of coins does Karen have than Shyla?

$  

Show Answers Only

`text($2.10 cents)`

Show Worked Solution
`text(Karen’s total)` `= text(Total mass)/text(mass of 1 coin) xx text(50 cents)`
  `= 307.65/14.65 xx 50`
  `= 21 xx 50`
  `= 1050\ text(cents)`

 

`text(Shyla’s total)` `= text(Total mass)/text(mass of 1 coin) xx text(20 cents)`
  `= 508.2/12.1 xx 20`
  `= 42 xx 20`
  `= 840\ text(cents)`

 

`:.\ text(Extra money)` `= 1050 – 840`
  `= 210\ text(cents)`
  `=$2.10`

Number, NAPX-p115611v01 SA

A 20-cent coin has a mass of 12.5 grams.

A 5-cent coin has a mass of 2.9 grams.

Harold has 487.5 grams of 20-cent coins.

Rick has 179.8 grams of 5-cent coins.

How much more worth of coins does Harold have than Rick, in cents?

  cents

Show Answers Only

`text(470 cents)`

Show Worked Solution
`text(Harold’s total)` `= text(Total mass)/text(mass 1 coin) xx text(20 cents)`
  `= 487.5/12.5 xx 20`
  `= 39 xx 20`
  `= 780\ text(cents)`

 

`text(Rick’s total)` `= text(Total mass)/text(mass of 1 coin) xx text(5 cents)`
  `= 179.8/2.9 xx 5`
  `= 62 xx 5`
  `= 310\ text(cents)`

 

`:.\ text(Extra money)` `= 780 – 310`
  `= 470\ text(cents)`

Number, NAP-L4-NC08

A table tennis club increased its membership by exactly 20% in the calendar year.

Select all of the following which could be the number of members the table tennis club had at the end of 2018.

24 35 40 52 66
 
 
 
 
 
Show Answers Only

`24 and 66`

Show Worked Solution

`text(Membership increase) = 1/5`

`=> 6/5 xx text(old membership = whole number)`

`=>\ text{Old membership (start of 2018) must finish in 5 or 0.}`

`text(Possible changes):`

`5 -> 6` `10 -> 12`
`15 -> 18` `20 -> 24`
`25 -> 30` `30 -> 36`
`35 -> 42` `40 -> 48`
`45 -> 54` `55 -> 66`

 
`:. 24, 66`

Number, NAP-L4-CA40 SA

A large can of pasta sauce weighs 550 grams and costs $3.95.

A small can of the same pasta sauce weighs 370 grams and costs $2.75.

How many cents cheaper, per 100 grams, is it to buy the large can of pasta sauce rather than the small can of pasta sauce?

Give your answer to one decimal place.

     cents
Show Answers Only

`2.5\ text(cents)`

Show Worked Solution

`text(Calculate price per 100 grams:)`

`text(Large can)` `= 3.95/5.5`
  `= 0.71818`
`text(Small can)` `= 2.75/3.7`
  `= 0.74324`

 

`text{Difference (per 100g)}` `= 0.74324 – 0.71818`
  `= 0.02506`
  `= 2.5\ text(cents)`

Number, NAP-L4-CA39 SA

At the start of a week, Miley had 2.59 GB of storage on her mobile phone.

During the week she downloaded 60 songs which each took up 6.5 MB of storage.

Miley also downloaded a TV show.

At the end of the week, she had 850 MB of storage left.
 

How many gigabytes of storage did the TV show use?

Give your answer as a decimal, to two decimal places.

    GB
Show Answers Only

`text(1.35 GB)`

Show Worked Solution

`text(Original storage = 2590 MB)`

COMMENT: Converting to megabytes simplifies calculations in this instance.

`text(Songs)` `= 60 xx 6.5`
  `= 390\ text(MB)`

 
`:.\ text(TV show size)`

`= 2590 – (390 + 850)`

`= 1350\ text(MB)`

`= 1.35\ text(GB)`

Measurement, NAP-L4-CA38

Josh used six identical triangular tiles to form a regular hexagon.

Each tile has an area of 4.8 cm².
 


 

Josh then adds more tiles to make a hexagon with double the side length of this hexagon.

What will be the area of this larger hexagon?

 
 
 
 
`9.6\ text(cm²)` `28.8\ text(cm²)` `57.6\ text(cm²)` `115.2\ text(cm²)`
Show Answers Only

`115.2\ text(cm²)`

Show Worked Solution

`text(Area of 1 triangle) = 4.8\ text(cm²)`

COMMENT: If sides increase by a factor of 2 (i.e. double), area increases by a factor of 4.

`text(Area of triangle with double side length)`

`= 4 xx 4.8`

`= 19.2\ text(cm²)`
 

`:.\ text(Area of larger hexagon)`

`= 6 xx 19.2`

`= 115.2\ text(cm²)`

Geometry, NAP-L4-CA37

Select the pair of similar triangles.

The triangles are not drawn to scale.

 
 
 
 
Show Answers Only

`text(Triangle 1 and 4)`

Show Worked Solution

`text(Similar triangles are equiangular.)`

`text(Calculate triangle angles of each option.)`

`text(Triangle 1: 55, 55, 70)`

`text(Triangle 2: 55, 65, 60)`

`text(Triangle 3: 50, 65, 65)`

`text(Triangle 4: 55, 55, 70)`

`:.\ text(Similar triangles have angles: 55, 55, 70)`

Statistics, NAP-L4-CA36

Wayne enters into a 10-lap motorcycle race.

He increases his speed each lap for the first 5 laps but has to make a pit stop during lap 6.

Wayne then resumes and increases his speed over the final 4 laps.

Which graph most accurately represents Wayne's 10-lap race?​
 

 
 
 
   
 
 
Show Answers Only

Show Worked Solution

`text(Laps 1 – 5:)`

`text(Increasing speed)\ ->\ text(graph trends down)`

`text(Lap 6:)`

`text(Pit stop)\ ->\ text(data point much higher)`

`:.\ text(Correct graph)`
 

Measurement, NAP-L4-CA35 SA

Shania breeds mice for her cancer research.

She measures the length of their bodies to the nearest tenth of a centimetre when they are 1 week old.

Shania records one mouse's body length as 6.8 centimetres.

What is the smallest measurement the actual body length of that mouse could be?

     centimetres
Show Answers Only

`6.75 text(cm)`

Show Worked Solution

`text(6.75 cm will be rounded up to 6.8 cm).`

`text(Anything shorter, like 6.74 cm, will be rounded)`

`text(down to 6.7 cm.)`

`:.\ text(The smallest measurement is 6.75 cm.)`

Measurement, NAP-L4-CA32

Angenie makes native American textiles.

She uses 16 identical leather equilateral triangles to make a headband.

The perimeter of each triangle is 12 centimetres.
 


 

What is the length of the headband?

 
 
 
 
 
32 centimetres 34 centimetres 64 centimetres 96 centimetres 102 centimetres
Show Answers Only

`34\ text(centimetres)`

Show Worked Solution

`text(Perimeter = 12 cm)\ \ =>\ \ text(1 side = 4 cm)`

`text(Length)` `= (8 xx 4)+(0.5 xx 4)`  
  `=34\ text(centimetres)`  

Number, NAP-L3-CA38 SA

At the start of a week, Miley had 2.59 GB of storage on her mobile phone.

During the week she downloaded 60 songs which each took up 6.5 MB of storage.

Miley also downloaded a TV show.

At the end of the week, she had 850 MB of storage left.
 

How many gigabytes of storage did the TV show use?

Give your answer as a decimal, to two decimal places.

    GB
Show Answers Only

`text(1.35 GB)`

Show Worked Solution

`text(Original storage = 2590 MB)`

`text(Songs)` `= 60 xx 6.5`
  `= 390\ text(MB)`

 
`:.\ text(TV show size)`

`= 2590 – (390 + 850)`

`= 1350\ text(MB)`

`= 1.35\ text(GB)`

Number, NAP-L4-CA34 SA

A laundromat can wash 12 loads of laundry in one hour at full capacity.

A standard load of laundry weighs 7 kilograms.

Here is some information about two different washing machines.
 


 

Working at full capacity, how many litres of water would the laundromat expect to save in one hour by using the front loader instead of the top loader?

    litres
Show Answers Only

`text(315 L)`

Show Worked Solution

`text(Top loader water used (1 load))`

`= 7 xx 10.25`

`= 71.75\ text(L)`
 

`text(Front loader water used (1 load))`

`= 7 xx 6.5`

`= 45.5\ text(L)`
 

`:.\ text(Expected water saved)`

`= 12 xx (71.75 – 45.5)`

`= 315\ text(L)`

Number, NAP-L3-CA36 SA

A laundromat can wash 12 loads of laundry in one hour at full capacity.

A standard load of laundry weighs 7 kilograms.

Here is some information about two different washing machines.
 


 

Working at full capacity, how many litres of water would the laundromat expect to save in one hour by using the front loader instead of the top loader?

    litres
Show Answers Only

`text(315 L)`

Show Worked Solution

`text(Top loader water used (1 load))`

`= 7 xx 10.25`

`= 71.75\ text(L)`
 

`text(Front loader water used (1 load))`

`= 7 xx 6.5`

`= 45.5\ text(L)`
 

`:.\ text(Expected water saved)`

`= 12 xx (71.75 – 45.5)`

`= 315\ text(L)`

Geometry, NAP-G3-CA29 SA

All lines of symmetry are drawn on a regular hexagon, pictured below.

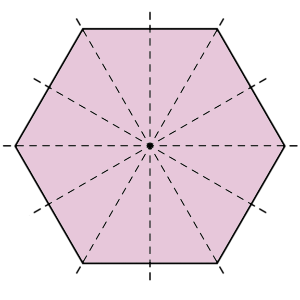
What is the size of the angle between each line of symmetry at the centre of the hexagon?
Show Answers Only

`30°`

Show Worked Solution

`text(There are 12 equal angles at the centre of the hexagon.)`

`:.\ text(Size of the angle)` `= 360 ÷ 12`
  `= 30°`

Number, NAP-K4-NC08 SA

The colour cerise is made by mixing red, green and blue paint in the ratio  `13 : 3 : 4`.

What is the volume, in litres, of green paint required if 6 litres of cerise paint is made?

Write your answer as a decimal.

     litres
Show Answers Only

`0.9\ text(litres)`

Show Worked Solution

`text(Ratio)\ 13:3:4`

`=>\ text(Fraction of green paint needed)`

`= 3/{(13 + 3 + 4)}`

`= 3/20`
 

`:.\ text(Volume of green paint)`

`= 3/20 xx 6`

`= 0.9\ text(litres)`

Algebra, NAP-K4-NC07

Nebula sells showbags at the Royal Easter show.

She sells two types, Star Wars and Toy Story showbags, for $10 each.

One day, she sell `x` Star Wars showbags and `y` Toy Story showbags.

Select all of the formulas below that Nebula could use to determine the correct amount of money collected on the day, in dollars.

 
 `10x + 10y`
 
 `10^2 xy`
 
 `20 (x + y)`
 
 `10 xy`
 
 `10 (x + y)`
Show Answers Only

`10x + 10y`

`10 (x + y)`

Show Worked Solution
`text(Money collected)` `= 10x + 10y`
  `= 10 (x + y)`

Number, NAP-K4-NC06 SA

Michael purchases a 3D printer worth $2 490 000.

He was given a 10% discount.

What was the price paid by Michael after the discount?

$    
Show Answers Only

`$2\ 241\ 000`

Show Worked Solution
`text(Discount)` `= 10% xx 2\ 490\ 000`
  `= $249\ 000`

 

`:.\ text(Price)` `= 2\ 490\ 000 – 249\ 000`
  `= $ 2\ 241\ 000`

Number, NAP-K3-NC08 SA

Michael purchases a 3D printer worth $2 490 000.

He was given a 10% discount.

What was the price paid by Michael after the discount?

$    
Show Answers Only

`$2\ 241\ 000`

Show Worked Solution
`text(Discount)` `= 10text(%) xx 2\ 490\ 000`
  `= 249\ 000`

 

`:.\ text(Price)` `= 2\ 490\ 000 – 249\ 000`
  `= $2\ 241\ 000`

Number, NAP-K3-CA40 SA

Bilbo and Legolas are planning a holiday for 5 days and 4 nights to Mordor.

They expect to spend $62 per person each day on food.

Their total accommodation cost is $183 per night.

They have already saved $250 each towards their holiday.

If they split the remaining cost equally, how much more will Bilbo and Legolas have to save each?

$    
Show Answers Only

`$426`

Show Worked Solution
`text(Food cost)` `= 5 xx (2 xx 62)`
  `= $620`
`text(Accommodation)` `= 183 xx 4`
  `= $732`

 

`text(Extra savings)` `= 620 + 732 – (2 xx 250)`
  `= $852\ text(total)`
  `= $426\ text(per person)`

Number, NAP-K3-CA39

A chemist sells 3 different sizes of cough mixture.
 

 
Ralph buys 0.7 litres of the cough mixture that includes at least one bottle of each size.

Select all of the combinations Ralph could have purchased.

 
 
 
 
Show Answers Only

`,\ text(and)`

Show Worked Solution

`text(Volume)` `= 180 + 120 +(4 xx 100)`
  `= 700\ text(mL)`
  `= 0.7\ text(L)`

 

`text(Volume)` `= 180 + 120 + 100 + 120 + 180`
  `= 700\ text(mL)`
  `= 0.7\ text(L)`

 

`text(Other options either don’t use one bottle of each size)`

`text(or don’t add up to 700 mL.)`

Number, NAP-K3-CA38

Lucretia writes 1197 as the product of its prime factors correctly.

Which expression does Lucretia write?

 
 `3 xx 21 xx 19`
 
 `3^2 xx 133`
 
 `3 xx 7 xx 57`
 
 `3^2 xx 7 xx 19`
Show Answers Only

`3^2 xx 7 xx 19`

Show Worked Solution

`text(Prime factors require all factors to be)`

`text(prime numbers:)`

`:. 3^2 xx 7 xx 19,\ \ text{(can also be written as}\ \ 3xx3xx7xx19)`

Number, NAP-K3-CA37 SA

Bert, Gary and Miles are weighing themselves.

Bert weighs 48.65 kilograms.

Gary weighs 0.3 kilograms more than Bert.

Miles weighs 0.75 kilograms less than Bert.

How many kilograms do the three boys weigh altogether?

    kilograms
Show Answers Only

`text(145.5 kg)`

Show Worked Solution

`text(Bert’s weight = 48.65 kg)`

`text(Gary’s weight = 48.65 + 0.3 = 48.95 kg)`

`text(Miles’ weight = 48.65 − 0.75 = 47.9 kg)`
 

`:.\ text(Total weight)` `= 48.65 + 48.95 + 47.9`
  `= 145.5\ text(kg)`

Number, NAP-K4-CA40 SA

Jagger makes and supplies fresh muffins to cafes in the city.

As the number of muffins he makes increases, the cost to make each muffin decreases.

He sells the muffins for the same price and takes the orders in multiples of 6.
 

 
Assuming the cost per muffin continues to follow the decreasing trend in the table, how much profit will Jagger make on an order of 30 muffins?

$  
Show Answers Only

`$132.00`

Show Worked Solution

`text(Sale price of 1 muffin)`

`= 31.50 ÷ 6`

`= $5.25`

 
`text{C} text{ost of 1 muffin (order of 30)}`

`= 1.00 – 0.15`

`= $0.85`
 

`:.\ text(Profit)` `= text(sales) – text(cost)`
  `= 30 xx 5.25 – 30 xx 0.85`
  `= $132.00`

Number, NAP-K4-CA39 SA

Dante deposits $5000 into a savings account which earns simple interest.

No deposits or withdrawals are made from this account.

After 4 years, Dante notices there is $5600 in the account.

What is the annual rate of interest for the account?

  %
Show Answers Only

`3text(%)`

Show Worked Solution
`text(Interest per year)` `= (5600 – 5000)÷4`
  `= 600 ÷ 4`
  `= $150`

 

`:.\ text(Interest rate)` `= 150/5000 xx 100`
  `= 3 text(%)`

Measurement, NAP-K4-CA38 SA

Leigh is making a stained glass window in the shape of a hexagon.

It uses aluminium bars for the frame and supports.

The supports are parallel with the sides of the frame, as shown below.
 

 
How many metres of aluminium bar are used to make this window?

   metres
Show Answers Only

`12\ text(m)`

Show Worked Solution
`text(Outside perimeter)` `= 4 xx 0.8 + 2 xx 0.6`
  `= 3.2 + 1.2`
  `= 4.4\ text(m)`

 
`text{(Note that through parallelogram properties, the top side)`

`text{width is half the width of the horizontal middle length.)}`

 
`text(Length of internal supports)`

`= 2 xx (4 xx 0.8) + 1.2`

`= 6.4 + 1.2`

`= 7.6\ text(m)`

 
`:.\ text(Total length of aluminium bar)`

`= 4.4 + 7.6`

`= 12\ text(m)`

Probability, NAP-K4-CA35 SA

A representative soccer team is chosen from 30 players who play for two clubs, Portland and Lithgow.

10 players from Portland and 20 players from Lithgow are playing in the trials, and 7 players from Portland and 8 from Lithgow are selected in the representative team.
 

 
One player at the trial is randomly selected.

What is the probability that the player is from Lithgow and is selected in the representative team?

Give your answer to two decimal places.
Show Answers Only

`0.27`

Show Worked Solution

`text{Pr(player is from Lithgow and selected)}`

`= text(number of possible players)/text(total players)`

`= 8/30`

`= 0.2666`

`= 0.27`

Probability, NAP-K4-CA37 SA

Cosette rolls a standard dice 100 times and records the results.

She calculates the experimental probability of rolling different numbers on this dice.

●   rolling an odd number 0.47
●   rolling a 4 0.15
●   not rolling a 6 0.88

 
What is the experimental probability of Cosette rolling a 2 on this dice?

 
Show Answers Only

`0.26`

Show Worked Solution

`Ptext{(rolling 4)}= 0.15`

`Ptext{(rolling 1, 3 or 5)}= 0.47`

`Ptext{(rolling 6)}` `= 1 -Ptext{(not rolling 6)}`
  `= 1 – 0.88`
  `= 0.12`

 
`text(S) text(ince probabilities sum to 1,)`

`Ptext{(rolling 2)}` `= 1 – (0.47 + 0.15 + 0.12)`
  `= 0.26`

Algebra, NAP-K4-CA34 SA

Jill is driving along a road at 60 km/h.

This graph shows stopping distance for different speeds.
 

 
Jill applies the brakes and comes to a stop.

If Jill is travelling at 75 km/h and brakes, how much extra distance does it take her to stop?

     m
Show Answers Only

`30\ text(m)`

Show Worked Solution

`text(From the graph,)`

`text(At 60 km/h, stopping distance = 45 m)`

`text(At 75 km/h, stopping distance = 75 m)`
 

`:.\ text(Extra distance)`

`= 75 – 45`

`= 30\ text(m)`

Geometry, NAP-K4-CA33 SA

Robin is designing a target with centre `O`.

The diameter of the smallest circle is 36 cm.
 

 
Robin makes  `AC = 1 1/4 xx AB`  and  `BC = 1/2 xx CD`.

What is the diameter of the whole target, `XD`?

     cm
Show Answers Only

`90\ text(cm)`

Show Worked Solution

`OB = 1/2 xx 36 = 18`

`AC = 1 1/4 xx 36 = 45`

`BC = 45 – 36 = 9`

`CD = 2 xx 9 = 18`

 

`:.\ text(Diameter)\ XD`

`= 2 xx text(radius)`

`= 2 xx (18 + 9 + 18)`

`= 90\ text(cm)`

Number, NAP-K3-CA35

A brand of pasta is sold in two different packets.
 

 
What is the difference in the price per kilogram of these two packets?

$1.50 $3.00 $3.60 $7.20
 
 
 
 
Show Answers Only

`$3.00`

Show Worked Solution

`text(Convert to price per kg)`

`text(Packet 1)`

`200\ text(g) = $1.80`

`1\ text(kg) = 5 xx 1.80 = $9`
 

`text(Packet 2)`

`750\ text(g) = $9`

`100\ text(g) = 9.00 ÷ 7.5 = $1.20`

`1\ text(kg) = 1.20 xx 10 = $12`
 

`:.\ text(Difference per kg)`

`= 12 – 9`

`= $3.00`

Measurement, NAP-K3-CA33 SA

A horse trough is in the shape of a rectangular prism, pictured below.
 

 
What is the capacity of the horse trough in litres?

    litres
Show Answers Only

`160`

Show Worked Solution

`text(Convert all measurements to metres.)`

`text(Volume)` `= 0.5 xx 0.4 xx 0.8`
  `= 0.16\ text(m³)`
  `= 160\ text{litres  (1 m³ = 1000 L)}`

Geometry, NAP-K4-CA32

Quadrilateral `ABCD` is drawn on a Cartesian plane.

The quadrilateral is rotated 90° anti-clockwise about the origin.

It is then reflected over the `y`-axis and labelled `A prime B prime C prime D prime`.

 
Which statement below is true?

 
 The coordinates of `A prime` are `(0, 1)`.
 
 `CD` is parallel to `C prime D prime`.
 
 The coordinates of `B prime` are `(2, 3)`.
 
 The quadrilateral `A prime B prime C prime D prime` is congruent to `ABCD`.
Show Answers Only

`text(The quadrilateral)\ A prime B prime C prime D prime\ text(is congruent to)\ ABCD`

Show Worked Solution

`text(Any reflection or rotation will maintain the same shape and)`

`text(therefore)\ A′B′C′D′\ text(is congruent to)\ ABCD.`

Number, NAP-K4-CA31

A grain silo is in the shape of a cylinder.

The silo has a diameter of 10 metres.

Grain is poured into an empty silo at a rate of 4 cubic metres per minute.
 

 
Approximately how long will it take to completely fill the silo?

`1 3/4\ text(hours)` `2 1/2\ text(hours)` `4\ text(hours)` `16\ text(hours)`
 
 
 
 
Show Answers Only

`4\ text(hours)`

Show Worked Solution

`text(Volume of cylinder)`

`= pi xx r^2 xx h`

`= pi xx 5^2 xx 12`

`~~ 942\ text(m³)`
 

`:.\ text(Time to fill silo)`

`~~ 942 ÷ 4`

`~~ 235\ text(mins)`

`~~ 4\ text(hours)`

Measurement, NAP-K4-CA30 SA

Hugo makes a rectangular prism by folding the net below.
 

 

What is the volume of Hugo's rectangular prism?

     cm³
Show Answers Only

`165\ text(cm³)`

Show Worked Solution

`text(Strategy 1)`

`text(By inspection, possible dimensions are:)`

`3 xx 11, 5 xx 11 and 3 xx 5`

`:.\ text(Volume)` `= 3 xx 11 xx 5`
  `= 165\ text(cm³)`

 
`text{Strategy 2 (Algebra)}`

`text(Dimensions of 3 rectangles are:)`

`x xx y = 33\ …\ (1) => y = 33/x …\ (1 prime)`

`x xx h = 55\ …\ (2) => h = 55/x …\ (2 prime)`

`y xx h = 15\ …\ (3)`

 
`text(Substitute)\ (1 prime) and (2 prime)\ text(into)\ (3)`

`33/x xx 55/x` `= 15`
`x^2` `= (33 xx 55)/15`
  `= 121`
`x` `= 11`

 
`=> y = 3, quad h = 5`
  

`:.\ text(Volume)` `= 3 xx 11 xx 5`
  `= 165\ text(cm³)`

Measurement, NAP-K4-CA26 SA

Percy has a large shower head which has a diameter of 25.5 centimetres.

What is the circumference of the shower head in centimetres, to one decimal place?
 


 

    cm
Show Answers Only

`80.1\ text(cm)`

Show Worked Solution
`text(Circumference)` `= pi xx d`
  `= pi xx 25.5`
  `= 80.110`
  `= 80.1\ text(cm)`

Statistics, NAP-K4-CA24 SA

A policeman is recording the speed of 25 cars travelling on a highway using a speed gun.

The results are shown in the stem-and-leaf plot.
 

What is the median speed?

    kilometres per hour
Show Answers Only

`119\ text(km/hr)`

Show Worked Solution

`25\ text(data points)`

`text(Median is the 13th data point)`

`:.\ text(Median) = 119\ text(km/hr)`

Geometry, NAP-D4-NC32 SA

Camilla is creating a sculpture using five similar triangles.
 

 
What is the size of the angle labelled `a^@`?

  degrees
Show Answers Only

`36^@`

Show Worked Solution

`text(Consider the centre angle of each triangle.)`

`5 xx x^@` `= 360 – 90\ \ text{(360° about a point)}`
`5x` `= 270`
`x` `= 54`
`:. a` `= 180 – (90 + 54)\ \ text{(angle sum of triangle)}`
  `= 36`

Geometry, NAP-F4-CA27 SA

Miko is designing a fan using similar triangles.
 

 
The edges of the largest and smallest triangles form a right angle.

What is the size of the angle marked `x^@`?

  degrees
Show Answers Only

`75^@`

Show Worked Solution

`text(Consider the top angles of each triangle,)\ a°`

`6 xx a^@` `= 90^@`
`a^@` `= 90 ÷ 6`
  `= 15^@`
`:. x^@` `= 180 – (15 + 90)\ \ text{(angle sum of triangle)}`
  `= 75^@`

Geometry, NAP-H3-NC31 SA

Kate cuts a solid prism with six faces in half to make two smaller identical prisms.

What is the least number of faces that one of the smaller prisms could have?

 
Show Answers Only

`5`

Show Worked Solution

`text(With 6 faces, prism must be a quadrilateral prism.)`

`text{Consider the top view of the prism (one example):}`

`text(Cut 1 will produce 2 triangular prisms with)`

`text(5 faces each.)`

`text(Cut 2 will produce 2 rectangular prisms with)`

`text(6 faces each.)`

`:. 5\ text(faces is the least.)`

Number, NAP-A3-NC32 SA

Helga uses the two conversion graphs below.
 

  
How many Australian dollars are equal in value to 50 British pounds

  Australian dollars
Show Answers Only

`160`

Show Worked Solution

`text{From the graph (left):}`

`50\ text(British pounds) = 125\ text(Canadian dollars)`

`text{From the graph (right):}`

`125\ text(Canadian dollars) = 160\ text(Australian dollars)`

Geometry, NAP-A3-CA32

Here is a map of Crikey Island.

The shortest distance from Point Nobby to Gilbos is 900 m.
 

 
The shortest distance from Point Nobby to Fire Beach is closest to

`text(1050 m)` `text(1900 m)` `text(2100 m)` `text(2450 m)`
 
 
 
 
Show Answers Only

`text(2100 m)`

Show Worked Solution

`text(Let)\ w =\ text(grid width)`

`text(Distance from Point Nobby to Gilbos) =4.5w`

`:. 4.5 w` `= 900`
`w` `= 200\ text(metres)`

 

`:.\ text(Distance from Point Nobby to Fire Beach)`

`= 10.5 w`

`= 10.5 xx 200`

`= 2100\ text(metres)`

Number, NAP-A3-NC31 SA

Maria puts 8 jelly beans in each of 7 party-bags.

She has 4 jelly beans left over.

Maria wants to put 9 jelly beans in each bag.

How many more jelly beans does she needs?

    jelly beans
Show Answers Only

`3`

Show Worked Solution

`text(Maria’s original number of jelly beans)`

`=7 xx8 +4`

`=60`
 

`text(Total jelly beans needed for 9 per bag)`

`=7 xx 9`

`=63`

 

`:.\ text(3 more jelly beans are needed.)`

Statistics, NAP-A4-NC31

This graph shows the number of goals a soccer team scored in a full season.
 

 
One match incorrectly recorded the team scoring no goals when they scored one.

What effect does this have on the mean and mode of the data?

 
 The mean decreases and the mode changes.
 
 The mean increases and the mode changes.
 
 The mean decreases and the mode does not change.
 
 The mean increases and the mode does not change.
Show Answers Only

`text(The mean increases and the mode does not change.)`

Show Worked Solution

`text(Total goals scored in the season increases by one.)`

`=>\ text(mean increases.)`

`text{The mode of 2 goals scored in a match (9 times)}`

`text(remains the mode after the change.)`

`:.\ text(The mean increases and the mode does not change.)`

Algebra, NAP-A4-NC30

The weight (`w` kilograms) and age (`a` years) of a turtle are related by the following inequality:

\begin{array} {|l|}
\hline
\rule{0pt}{2.5ex}w < 8a-13\ \  \text{for all values of}\ a\ \text{between 1 and 10}\rule[-1ex]{0pt}{0pt} \\
\hline
\end{array}

Which pair of values satisfy this inequality?

 
 `w = 4 and a = 2`
 
 `w = 12 and a = 3`
 
 `w = 18 and a = 4`
 
 `w = 40 and a = 6`
Show Answers Only

`w = 18 and a = 4`

Show Worked Solution

`text(Test each option by trial and error.)`

`text(Consider)\ \ w = 18,\ a = 4:`

`18 < 8 xx 4-13`

`18 < 19\ \ text{(correct)}`

 

`:. w = 18,\ a = 4\ text(satisfies the equation).`

Number, NAP-A4-NC29 SA

On Thursday Banjo read 30% of a book.

On Friday he read half of the remaining pages of the book.

What percentage of the whole book has Banjo read over the two nights, in total?

  %
Show Answers Only

`text(65%)`

Show Worked Solution

`text(Fraction read on Thursday)\ = 3/10`

`text(Fraction read on Friday)`

=`1/2 xx 7/10 = 7/20`

 

`:.\ text(Total read over 2 nights)`

`= 3/10 + 7/20`

`= 6/20 + 7/20`

`= 13/20`

`= 65 text(%)`

Statistics, NAP-A4-CA32

A survey asked 9 students in Year 7 how many times they had travelled overseas.
 

 

 
Which of the following is true for this data?

 
 mean > median > mode
 
 mean > median < mode
 
 mean = median = mode
 
 mean = median > mode
Show Answers Only

`text(mean = median > mode)`

Show Worked Solution

`text(Mode = 2)`

`text(Median = 5th number = 3)`

`text(Mean)` `= (0 + 2 + 2 + 2 + 3 + 4 + 4 + 5 + 5)/9`
  `= 27 ÷ 9`
  `= 3`

 

`:.\ text(mean = median > mode)`

Algebra, NAP-A4-CA31 SA

The cost in dollars to make `w` Star Wars toy figures is  `3500 + 10w`.

How many Star Wars toy figures can be made for a cost of $25 000.

    toy figures
Show Answers Only

`2150`

Show Worked Solution

`text(Number of toy figures)`

`3500 + 10w` `= 25\ 000`
`10w` `= 21\ 500`
`:. w` `= (21\ 500)/10`
  `= 2150`

Geometry, NAP-A4-CA29 SA

This is a diagram of the course for a 40 km bike road race.

The riders start and finish at the Start Gate.
 

 

 What is the distance between the Starting Gate and the Fork?

    km
Show Answers Only

`9.1\ text(km)`

Show Worked Solution
`text(Distance)` `= 1/2 xx [40 – (7.51 + 8.38 + 5.91)]`
  `= 1/2 xx (40 – 21.8)`
  `= 1/2 xx 18.2`
  `= 9.1\ text(km)`