SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Algebra, STD2 A2 2012 HSC 5 MC

The line  `l`  has intercepts  `p`  and  `q`,  where  `p`  and  `q`  are positive integers. 
  

What is the gradient of line  `l ` ? 

  1. `-p/q`  
  2. `-q/p`  
  3. `\ \ \ p/q`  
  4. `\ \ \ q/p`  
Show Answers Only

`A`

Show Worked Solution
 
♦ Mean mark 45%
`text(Gradient)` `= text(rise)/text(run)`
  `= -p/q`

`=>  A`

Probability, 2UG 2012 HSC 3 MC

A pair of players is to be selected from 6 people.

How many different pairs of players can be selected?

(A)   `6`

(B)  `12`  

(C)  `15` 

(D)  `30` 

Show Answers Only

`C`

Show Worked Solution
♦ Mean mark 40%
COMMENT: Calculating #combinations involving unordered pairs has proven very challenging to a majority of students in past exams. Ensure you understand this concept.

`text(Arrangements of)\ \ 2 = 2 xx 1 = 2`

`text(# Different pairs)\ \ = (6xx5)/(2xx1) = 15`

`=>  C`

 

Measurement, STD2 M1 2013 HSC 25 MC

A net is made using four rectangles and two trapeziums. It is folded to form a solid.
  

 What is the volume of the solid, in cm3 ?

  1. `360\ text(cm)^3`
  2. `434\ text(cm)^3`
  3. `440\ text(cm)^3`
  4. `576\ text(cm)^3`
Show Answers Only

`D`

Show Worked Solution

`text(Volume)=Ah\ \ \ text(where)\ \ A\ text(is the area of a trapezium)`

♦ Mean mark 35%
COMMENT: Note that `h` in the “area” formula is different to the `h` used in the “volume” formula.
`A` `=1/2 h(a+b)`
  `=1/2xx8(11+5)`
  `=64\ text(cm²)`

 

`:.V=Ah=64xx9=576\ text(cm³)`

`=>  D`

Measurement, STD2 M6 2013 HSC 24 MC

What is the value of  `theta`,  to the nearest degree?

2013 24 mc

  1.    `21^@`
  2.    `32^@`
  3.    `43^@`
  4.    `55^@`
Show Answers Only

`C`

Show Worked Solution
`a/sinA` `=b/sinB`
`82/sinA` `=100/sin26`
`sin A` `=(82 xx sin26)/100`
  `=0.35946…`
`/_A` `=21^@\ \ \ \ text{(nearest degree)}`

 
`text(S)text(ince)\   180^@\ text(in)\ Delta:`

`90+26+(theta+21)` `=180`
`theta` `=43^@`

 
`=>  C`

Algebra, STD2 A1 2013 HSC 21 MC

Which equation correctly shows  `r`  as the subject of  `S=800(1-r)`?

  1. `r=(800-S)/800`
  2. `r=(S-800)/800`
  3. `r=800-S`
  4. `r=S-800`
Show Answers Only

`A`

Show Worked Solution
♦♦♦ Mean mark 27%
`S` `=800(1-r)`
`1-r` `=S/800`
`r` `=1-S/800`
  `=(800-S)/800`

 
`=>\ A`

Probability, STD2 S2 2013 HSC 18 MC

Two unbiased dice, each with faces numbered  1, 2, 3, 4, 5, 6,  are rolled.

What is the probability of obtaining a sum of 6?

  1. `1/6`
  2. `1/12`
  3. `5/12`
  4. `5/36`
Show Answers Only

`D`

Show Worked Solution

`text(Total outcomes)=6xx6=36`

`text{Outcomes that sum to 6}=text{(1,5) (5,1) (2,4) (4,2) (3,3)} =5`

`:.\ P\text{(sum of 6)} =5/36`

`=>\ D`

♦♦ Mean mark 35%.

Measurement, STD2 M1 2013 HSC 17 MC

Triangles  `ABC`  and  `DEF`  are similar.
  

Which expression could be used to find the value of  `x`?

  1. `yxx10/15`
  2. `yxx10/23`
  3. `yxx15/10`
  4. `yxx23/15`
Show Answers Only

`C`

Show Worked Solution
♦ Mean mark 38%

`text(We know)\ \ Delta ABC\ text(|||)\ Delta DEF`

`:.\ (AB)/(AC)` `=y/10=(DE)/(DF)=x/15`
`x/15` `=y/10`
`x` `=yxx15/10`

 
`=> C`

Financial Maths, STD2 F1 2013 HSC 11 MC

An enterprise agreement has the following annual salary arrangements:
 

George's employer pays 6% more than the enterprise agreement. He is on Step 3 and receives an allowance for Leader 2.

What is George's gross monthly pay?

  1. $4375.00
  2. $4412.50
  3. $4600.00
  4. $4637.50
Show Answers Only

`D`

Show Worked Solution
♦ Mean mark 46%
`text(Gross annual pay)` `=(45\ 000+7500)xx1.06`
  `=$55\ 650`

 

`:.\ text(Gross monthly pay)` `=(55\ 650)/12`
  `=$4637.50`

 
`=>\ D`

Calculus, 2ADV C3 2008 HSC 10b

 

The diagram shows two parallel brick walls  `KJ`  and  `MN`  joined by a fence from  `J`  to  `M`.  The wall  `KJ`  is  `s`  metres long and  `/_KJM=alpha`.  The fence  `JM`  is  `l`  metres long.

A new fence is to be built from  `K`  to a point  `P`  somewhere on  `MN`.  The new fence  `KP`  will cross the original fence  `JM`  at  `O`.

Let  `OJ=x`  metres, where  `0<x<l`.

  1. Show that the total area,  `A`  square metres, enclosed by  `DeltaOKJ`  and  `DeltaOMP`  is given by
     
         `A=s(x-l+l^2/(2x))sin alpha`.   (3 marks)

  2. Find the value of  `x`  that makes  `A`  as small as possible. Justify the fact that this value of  `x`  gives the minimum value for  `A`.  (3 marks)

  3. Hence, find the length of  `MP`  when  `A`  is as small as possible.    (1 mark)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `l/sqrt2`
  3. `(sqrt2-1)s\ \ text(metres)`
Show Worked Solution
i.

`A=text(Area)\  Delta OJK+text(Area)\ Delta OMP`

♦♦♦ Low mean marks highlighted (although exact data not available before 2009).

`text(Using sine rule)`

`text(Area)\ Delta OJK=1/2\ x s sin alpha` 

`text(Area)\ DeltaOMP =>text(Need to find)\ \ MP`

`/_OKJ` `=/_MPO\ \ text{(alternate angles,}\ MP\ text(||)\ KJtext{)}`
`/_PMO` `=/_OJK=alpha\ \ text{(alternate angles,}\ MP\ text(||)\ KJtext{)}`

 
`:.\ DeltaOJK\ text(|||)\ Delta OMP\ \ text{(equiangular)}`

`=>x/s` `=(l-x)/(MP)\ ` ` text{(corresponding sides of similar triangles)}`
`MP` `=(l-x)/x *s`  
`text(Area)\ Delta\ OMP` `=1/2 (l-x)* MP * sin alpha`
  `=1/2 (l-x)*((l-x))/x* s  sin alpha`
`:. A`  `=1/2 x*s sin alpha+1/2 (l-x)*((l-x))/x* s sin alpha`
  `=s sin alpha(1/2 x+1/2 (l-x)*((l-x))/x)`
  `=s sin alpha(1/2 x+(l-x)^2/(2x))`
  `=s sin alpha(1/2 x+l^2/(2x)-l+1/2 x)`
  `=s(x-l+l^2/(2x))sin alpha\ \ \ \ text(… as required)`

 

ii.   `text(Find)\ x\ text(such that)\ A\ text(is a minimum)`

MARKER’S COMMENT: Students who could not complete part (i) are reminded that they can still proceed to part (ii) and attempt to differentiate the result given.
Note that `l` and `alpha` are constants when differentiating. 
`A` `=s(x-l+l^2/(2x))sin alpha`
`(dA)/(dx)` `=s(1-l^2/(2x^2))sin alpha`

`text(MAX/MIN when)\ (dA)/(dx)=0`

`s(1-l^2/(2x^2))sin alpha` `=0`
`l^2/(2x^2)` `=1`
`2x^2` `=l^2`
`x^2` `=l^2/2`
`x` `=l/sqrt2,\ \ \ x>0`

 

`(d^2A)/(dx^2)=s((l^2)/(2x^3))sin alpha`

`text(S)text(ince)\ \ 0<alpha<90°\ \ =>\ sin alpha>0,\ \ l>0\ \ text(and)\ \  x>0`

`(d^2A)/(dx^2)>0\ \ \ =>text(MIN at)\ \ x=l/sqrt2`

 

iii.   `text(S)text(ince)\ \ MP=((l-x))/x s\ \ text(and MIN when)\ \ x=l/sqrt2`

`MP` `=((l-l/sqrt2)/(l/sqrt2))s xx sqrt2/sqrt2`
  `=((sqrt2 l-l))/l s`
  `=(sqrt2-1)s\ \ text(metres)`

 

`:.\ MP=(sqrt2-1)s\ \ text(metres when)\ A\ text(is a MIN.)`

Calculus, 2ADV C3 2009 HSC 9b

An oil rig,  `S`,  is 3 km offshore. A power station,  `P`,  is on the shore. A cable is to be laid from `P`  to  `S`.  It costs $1000 per kilometre to lay the cable along the shore and $2600 per kilometre to lay the cable underwater from the shore to  `S`.

The point  `R`  is the point on the shore closest to  `S`,  and the distance  `PR`  is 5 km.

The point  `Q`  is on the shore, at a distance of  `x`  km from  `R`,  as shown in the diagram.


  

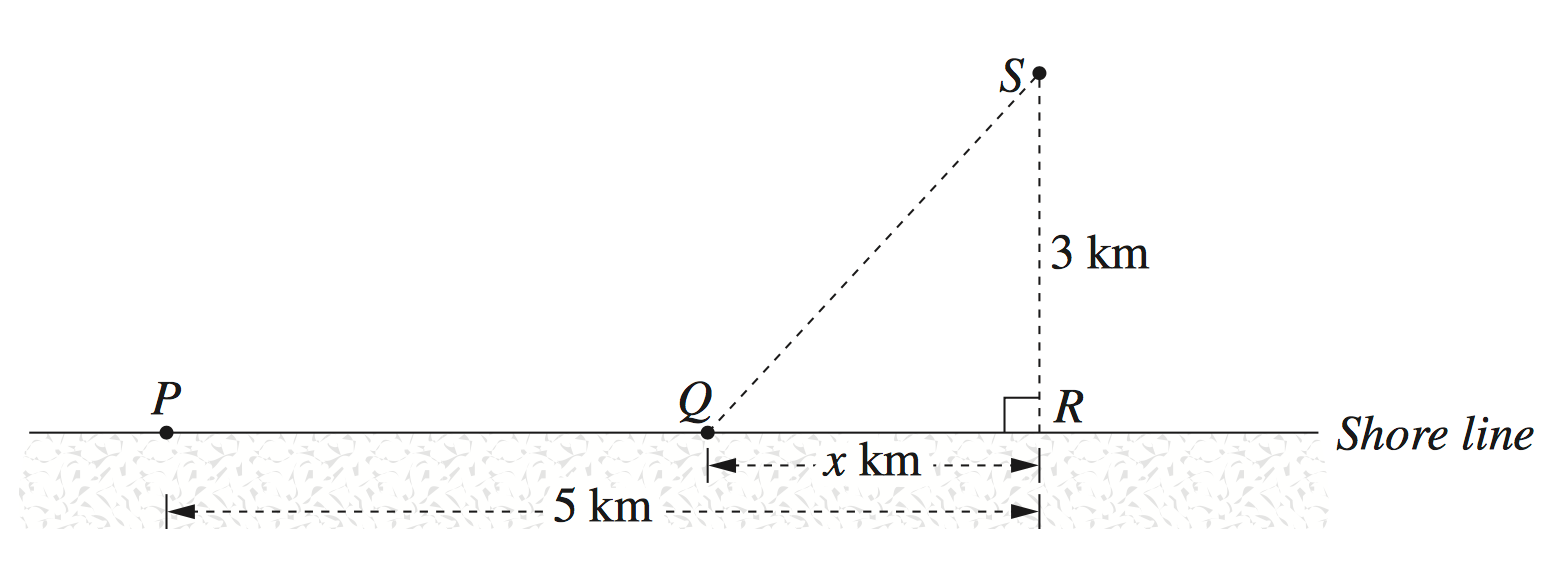
  1. Find the total cost of laying the cable in a straight line from  `P`  to  `R`  and then in a straight line from  `R`  to  `S`.   (1 mark)

  2. Find the cost of laying the cable in a straight line from  `P`  to  `S`.  (1 mark)

  3. Let  `$C`  be the total cost of laying the cable in a straight line from  `P`  to  `Q`,  and then in a straight line from `Q`  to  `S`.
     
    Show that  `C=1000(5-x+2.6sqrt(x^2+9))`.    (2 marks)

  4. Find the minimum cost of laying the cable.    (4 marks)

  5. New technology means that the cost of laying the cable underwater can be reduced to $1100 per kilometre.

     

    Determine the path for laying the cable in order to minimise the cost in this case.    (2 marks)

Show Answers Only
  1. `$12\ 800`
  2. `$15\ 160`
  3. `text{Proof (See Worked Solutions)}`
  4. `$12\ 200`
  5. `P\ text(to)\  S\ text(in a straight line.)`
Show Worked Solution
♦♦ Although specific data is unavailable for question parts, mean marks were 35% for Q9 in total.
i.   `text(C)text(ost)` `=(PRxx1000)+(SRxx2600)`
  `=(5xx1000)+(3xx2600)`
  `=12\ 800`

 
`:. text(C)text(ost is)\   $12\ 800`

 

ii.   `text(C)text(ost)=PSxx2600`

`text(Using Pythagoras:)`

`PS^2` `=PR^2+SR^2`
  `=5^2+3^2`
  `=34`
`PS` `=sqrt34`

 

`:.\ text(C)text(ost)` `=sqrt34xx2600`
  `=15\ 160.474…`
  `=$15\ 160\ \ text{(nearest dollar)}`

 

iii.  `text(Show)\ \ C=1000(5-x+2.6sqrt(x^2+9))`

`text(C)text(ost)=(PQxx1000)+(QSxx2600)`

`PQ` `=5-x`
`QS^2` `=QR^2+SR^2`
  `=x^2+3^2`
`QS` `=sqrt(x^2+9)`
`:.C` `=(5-x)1000+sqrt(x^2+9)\ (2600)`
  `=1000(5-x+2.6sqrt(x^2+9))\ \ text(…  as required)`

 

iv.   `text(Find the MIN cost of laying the cable)`

`C` `=1000(5-x+2.6sqrt(x^2+9))`
`(dC)/(dx)` `=1000(–1+2.6xx1/2xx2x(x^2+9)^(–1/2))`
  `=1000(–1+(2.6x)/(sqrt(x^2+9)))`

`text(MAX/MIN when)\ (dC)/(dx)=0`

IMPORTANT: Tougher derivative questions often require students to deal with multiple algebraic constants. See Worked Solutions in part (iv).

`1000(–1+(2.6x)/(sqrt(x^2+9)))=0`

`(2.6x)/sqrt(x^2+9)` `=1`
`2.6x` `=sqrt(x^2+9)`
`(2.6)^2x^2` `=x^2+9`
`x^2(2.6^2-1)` `=9`
`x^2` `=9/5.76`
  `=1.5625`
`x` `=1.25\ \ \ \ (x>0)`
MARKER’S COMMENT: Check the nature of the critical points in these type of questions. If using the first derivative test, make sure some actual values are substituted in.

`text(If)\ \ x=1,\ \ (dC)/(dx)<0`

`text(If)\ \ x=2,\ \ (dC)/(dx)>0`

`:.\ text(MIN when)\ \ x=1.25`

`C` `=1000(5-1.25+2.6sqrt(1.25^2+9))`
  `=1000(122)`
  `=12\ 200` 

 

`:.\ text(MIN cost is)\  $12\ 200\ text(when)\   x=1.25`

 

v.   `text(Underwater cable now costs $1100 per km)`

`=>\ C` `=1000(5-x)+1100sqrt(x^2+9)`
  `=1000(5-x+1.1sqrt(x^2+9))`
`(dC)/(dx)` `=1000(–1+1.1xx1/2xx2x(x^2+9)^(-1/2))`
  `=1000(–1+(1.1x)/sqrt(x^2+9))`

 
`text(MAX/MIN when)\ (dC)/(dx)=0`

`1000(–1+(1.1x)/sqrt(x^2+9))` `=0`
`(1.1x)/sqrt(x^2+9)` `=1`
`1.1x` `=sqrt(x^2+9)`
`1.1^2x^2` `=x^2+9`
`x^2(1.1^2-1)` `=9`
`x^2` `=9/0.21`
`x` `~~6.5\ text{km (to 1 d.p.)}`
  `=>\ text(no solution since)\ x<=5`

 
`text(If we lay cable)\ PR\ text(then)\ RS`

MARKER’S COMMENT: Many students failed to interpret a correct calculation of  `x>5`  as providing no solution.

`=>\ text(C)text(ost)=5xx1100+3xx1000=8500`

`text(If we lay cable directly underwater via)\ PS`

`=>\ text(C)text(ost)=sqrt34xx1100=6414.047…`

`:.\ text{MIN cost is  $6414 by cabling directly from}\ P\ text(to)\ S`.

Calculus, 2ADV C3 2010 HSC 5a

A rainwater tank is to be designed in the shape of a cylinder with radius  `r`  metres and height  `h`  metres.

2010 5a

The volume of the tank is to be 10 cubic metres. Let  `A`  be the surface area of the tank, including its top and base, in square metres.

  1. Given that  `A=2pir^2+2pi r h`,   show that  `A=2 pi r^2+20/r`.   (2 marks)

  2. Show that  `A`  has a minimum value and find the value of  `r`  for which the minimum occurs.  (3 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `r~~1.17\ text(metres)`
Show Worked Solution

i.    `text(Show)\ A=2 pi r^2+20/r`

MARKER’S COMMENT: Students MUST know the volume formula for a cylinder. Those that did and stated `10=pi r^2 h` most often completed this question efficiently.

`text(S)text(ince)\ V=pi r^2h=10\ \ \ \ =>\ h=10/(pi r^2)`

`text(Substituting into)\ A`

`A` `= pi r^2+2 pi r (10/(pi r^2))`
  `=2 pi r^2+20/r\ \ \ text(…  as required)`

 

♦ Mean mark 44%
MARKER’S COMMENT: The “table method” or 1st derivative test for proving a minimum (i.e. showing how `(dA)/(dr)` changes sign) was also quite successful.
ii. `A`  `=2 pi r^2+20/r`
  `(dA)/(dr)` `=4 pi r-20/r^2`
  `(d^2A)/(dr^2)` `=4 pi+40/r^3>0\ \ \ \ \ (r>0)`

 
`=>\ text(MIN occurs when)\ \ (dA)/(dr)=0`

`4 pi r-20/r^2` `=0`
`4 pi r^3-20` `=0`
`4 pi r^3` `=20`
`r` `=root3 (5/pi)`
  `=1.16754…`
  `=1.17\ text{metres  (2 d.p.)}`

Calculus, 2ADV C3 2011 HSC 10b

A farmer is fencing a paddock using  `P`  metres of fencing. The paddock is to be in the shape of a sector of a circle with radius  `r`  and sector angle `theta`  in radians, as shown in the diagram.

2011 10b

  1. Show that the length of fencing required to fence the perimeter of the paddock is
      
       `P=r(theta+2)`.    (1 mark)

  2. Show that the area of the sector is  `A=1/2 Pr-r^2`.    (1 mark) 

  3. Find the radius of the sector, in terms of  `P`, that will maximise the area of the paddock.    (2 marks)

  4. Find the angle  `theta`  that gives the maximum area of the paddock.    (1 mark)

  5. Explain why it is only possible to construct a paddock in the shape of a sector if
     
         `P/(2(pi+1)) <\ r\ <P/2`   (2 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `text{Proof  (See Worked Solutions)}`
  3. `r=P/4`
  4. `2\ text(radians)`
  5. `text{Proof  (See Worked Solutions)}`
Show Worked Solution

i.   `text(Need to show)\ \ P=r(theta+2)`

`P` `=(2xxr)+theta/(2pi)xx2pir`
  `=2r+ r theta`
  `=r(theta+2)\ \ text(…  as required)`

 

ii.   `text(Need to show)\ \ A=1/2 Pr-r^2`.

`text(S)text(ince)\ \ P=r(theta+2)\ \ \ =>\ theta=(P-2r)/r`

♦ Mean mark 41%.
TIP: Area of a sector `=pi r^2 xx` the percentage of the circle that the sector angle accounts for, i.e. `theta/(2 pi)` radians. `:. A=pi r^2“ xx theta/(2 pi)=1/2 r^2 theta`.
`:. A` `=1/2 r^2 theta`
  `=1/2 r^2*(P-2r)/r`
  `=1/2(Pr-2r^2)`
  `=1/2 Pr-r^2\ \ text(…  as required)`

 

iii.  `A=1/2 Pr-r^2`

♦♦ Mean mark 29%
MARKER’S COMMENT: The second derivative test proved much more successful and easily proven in this part. Make sure you are comfortable choosing between it and the 1st derivative test depending on the required calcs.

`(dA)/(dr)=1/2 P-2r`

`text(MAX or MIN when)\ \ (dA)/(dr)=0`

`1/2 P-2r` `=0`
`2r` `=1/2 P`
`r` `=P/4`

 
`(d^2A)/(dr^2)=-2\ \ \ \ =>text(MAX)`

`:.\ text(Area is a MAX when)\ r=P/4\ text(units)`

 

iv.   `text(Need to find)\ theta\ text(when area is a MAX)\ =>\ r=P/4`

♦♦♦ Mean mark 20%
`P` `=r(theta+2)`
  `=P/4(theta+2)`
`4P` `=P(theta+2)`
`theta+2` `=4`
`theta` `=2\ text(radians)`

 

v.  `text(For a sector to exist)\ \ 0<\ theta\ <2pi, \ \ text(and)\ \ theta=(P-2r)/r`

♦♦♦ Mean mark 4%. A BEAST!
MARKER’S COMMENT: When asked to ‘explain’, students should support their answer with a mathematical argument.
`=>(P-2r)/r` `>0`
`P-2r` `>0`
`r` `<P/2`
`=>(P-2r)/r` `<2pi`
`P-2r` `<2r pi`
`2r pi+2r` `>P`
`2r(pi+1)` `>P`
`r` `>P/(2(pi+1))`

 

`:.P/(2(pi+1)) <\ r\ <P/2\ \ text(…  as required)`

Mechanics, EXT2* M1 2009 HSC 6a

Two points, `A` and `B`,  are on cliff tops on either side of a deep valley. Let `h` and `R` be the vertical and horizontal distances between `A` and `B` as shown in the diagram. The angle of elevation of `B` from `A` is  `theta`,  so that  `theta=tan^-1(h/R)`.
 

2009 6a
 

At time `t=0`,  projectiles are fired simultaneously from `A` and `B`.  The projectile from `A` is aimed at `B`, and has initial speed `U` at an angle of  `theta`  above the horizontal. The projectile from `B` is aimed at `A` and has initial speed `V` at an angle  `theta`  below the horizontal.

The equations of motion for the projectile from `A` are

`x_1=Utcos theta`   and   `y_1=Utsin theta-1/2 g t^2`,

and the equations for the motion of the projectile from `B` are

`x_2=R-Vtcos theta`   and   `y_2=h-Vtsin theta-1/2 g t^2`,     (DO NOT prove these equations.)

  1. Let `T` be the time at which  `x_1=x_2`.
     
    Show that  `T=R/((U+V)\ cos theta)`.   (1 mark)

  2. Show that the projectiles collide.    (2 marks)

  3. If the projectiles collide on the line  `x=lambdaR`,  where  `0<lambda<1`,  show that
     
         `V=(1/lambda-1)U`.    (1 mark)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}` 
  2. `text{Proof  (See Worked Solutions)}`
  3. `text{Proof  (See Worked Solutions)}`
Show Worked Solution

i.   `text(Let)\ \ x_1=x_2\ \ text(at)\ \ t=T`

`UTcos theta` `=R-VTcos theta`
`UTcos theta+VTcos theta` `=R`
`Tcos theta\ (U+V)` `=R`

 
 `:. T=R/((U+V)\ cos theta)\ \ text(… as required)`

 

ii.   `text(If particles collide,)\ \  y_1=y_2\ \ text(at)\ \ t=T`

♦♦♦ Mean mark data not available although “few” students were able to complete this part.
MARKER’S COMMENT: Better responses showed  `y_1=y_2`,  or  `y_1-y_2=0`  which eliminated  `–½ g t^2`  from the algebra. Substituting `tan theta=h//R` was a key element in completing this proof.
`y_1` `=UTsin theta-1/2 g T^2`
  `=(UR sin theta)/((U+V)\ cos theta)-1/2 g T^2`
`y_2` `=h-VTsin theta-1/2 g T^2`
  `=Rtan theta-(VR sin theta)/((U+V)\ cos theta)-1/2 g T^2`
  `=R(((sin theta/cos theta)(U+V) cos theta-V sin theta)/((U+V)\ cos theta))-1/2 g T^2`
  `=R/((U+V)\ cos theta)(Usin theta+Vsin theta-Vsin theta)-1/2 g T^2`
  `=(UR sin theta)/((U+V)\ cos theta)-1/2 g T^2`
  `=y_1`

 

`:.\ text(Particles collide since)\  y_1=y_2\ text(at)\ t=T`.

 

iii.  `text(Particles collide on line)\ \ x=lambdaR,\ text(i.e.  where)\ \ t=T`

MARKER’S COMMENT: Students must show sufficient working in proofs to convince markers they have derived the answer themselves.
`lambdaR` `=UTcos theta`
  `=U R/((U+V)\ cos theta)cos theta`
  `=(UR)/((U+V))`
`(U+V)(lambdaR)` `=UR`
`U+V` `=(UR)/(lambdaR)`
`V` `=U/lambda-U`
  `=(1/lambda-1)U\ \ text(… as required)`

Mechanics, EXT2* M1 2010 HSC 6b

A basketball player throws a ball with an initial velocity  `v`  m/s at an angle of  `theta`  to the horizontal. At the time the ball is released its centre is at  `(0,0)`, and the player is aiming for the point `(d,h)`  as shown on the diagram. The line joining  `(0,0) `  and  `(d,h)`  makes an angle  `alpha`  with the horizontal, where  `0<alpha<pi/2`.
 

6b
 

Assume that at time  `t`  seconds after the ball is thrown its centre is at the point  `(x,y)`,  where

`x=vtcos theta`

`y=vt sin theta-5 t^2`.      (DO NOT prove this.)

  1. If the centre of the ball passes through  `(d,h)`  show that
     
         `v^2=(5d)/(cos theta sin theta-cos^2 theta tan alpha)`    (3 marks)

    (2) What happens to  `v`  as  `theta\ ->pi/2` ?    (1 mark)

  2. For a fixed value of  `alpha`,  let  `F(theta)=cos theta sin theta-cos^2 theta tan alpha`.
     
    Show that  `F prime(theta)=0`   when   `tan2theta tan alpha=-1`  (2 marks)

  3. Using part (a)(ii)* or otherwise show that  `F prime(theta)=0`,   when  `theta=alpha/2+pi/4`.    (1 mark)

     

    *Please note for the purposes of this question, part (a)(ii) showed that  when  `tanA tanB=-1`,  then  `A-B=pi/2` 

  4. Explain why  `v^2`  is a minimum when  `theta=alpha/2+pi/4`     (2 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}` 
  2. (1)  `v->oo`

     

    (2)  `v->oo`

  3. `text{Proof  (See Worked Solutions)}`
  4. `text{Proof  (See Worked Solutions)}` 
  5. `text{Explanation  (See Worked Solutions)}`
Show Worked Solution

i.   `text(Ball passes through)\ \ (d,h).`

`text(Find)\ t\ text(when)\ x=d :`

♦ Mean mark 43%
IMPORTANT: It is critical to use the relationship `tan alpha=h/d` to achieve the required proof.
`d` `=vtcos theta`
`:. t` `=d/(vcos theta)`

 

`text(S)text(ince)\ \ y=h\ \ text(when)\ \ t=d/(vcos theta)`

`h` `=vtsin theta-5t^2`
  `=v(d/(vcos theta))sin theta-5(d^2)/(v^2cos^2 theta)`
`(5d^2)/(v^2cos^2 theta)` `=(dsin theta)/cos theta-h`
`(5d^2)/v^2` `=dsin theta cos theta-cos^2 thetaxxh`
`v^2/(5d^2)` `=1/(dsin theta cos theta-cos^2 thetaxxh)`
`v^2` `=(5d^2)/(dsin theta cos theta-cos^2 thetaxxh)`
  `=(5d)/(cos theta sin theta-cos^2 thetaxxh/d)`
  `=(5d)/(cos theta sin theta-cos^2 theta tan alpha)\ \ text(… as required)`

 

 

ii. (1)  `text(As)\ \  theta->alpha`

♦ Mean marks of 37% and 32% for parts (ii)(1) and (ii)(2) respectively.

`costheta sin theta-cos^2 theta tan alpha->0`

`v->oo`

ii. (2)  `text(As)\ \  theta->pi/2`

`cos theta sin theta-cos^2 theta tan theta->0`

`v->oo`

 

iii.  `text(Show)\ \ tan 2thetatan alpha=–1\ \ text(when)\ \ F prime(theta)=0`.

`F(theta)` `=costheta sin theta-cos^2theta tan alpha`
`F prime(theta)` `=cos theta costheta+sin theta (–sin theta)-2cos theta (–sin theta) tan alpha`
  `=cos^2 theta-sin^2 theta+sin 2theta tan alpha`
  `=cos 2theta+sin 2theta tan alpha`

 

`text(When)\ F prime(theta)=0`

♦♦ Mean mark part (iii) 21%
MARKER’S COMMENT: Many students failed to treat  `tan alpha` as a constant when differentiating.
`cos 2theta+sin2thetatan alpha` `=0`
`sin2thetatan alpha` `=-cos2theta`
`tan 2theta tan alpha` `=-1\ \ text(… as required)`

 

iv.  `text(Show that)\ \ F prime(theta)=0,\ \ text(when)\ \ theta=alpha/2+pi/4`

`text(If)\ \ tanA tanB=–1\ => A-B=pi/2`

`text{(Given in part (a)(ii) – see note in question)}`

 

`text(S)text(ince)\ \ tan2theta tan alpha=–1\ \ text{(see part (iii))}`

♦♦♦ Mean mark 14%
MARKER’S COMMENT: Linking part (a)(ii) to this solution was a feature of the more efficient and successful approaches.
`=>\ \ 2theta-alpha` `=pi/2`
`2theta` `=alpha+pi/2`
`theta` `=alpha/2+pi/4`

 

 `text(Given that)\ \ Fprime(theta)=0\ \ text(when)\ \ tan 2thetatan alpha=–1`

`:. Fprime(theta)=0\ \ text(when)\ \ theta=alpha/2+pi/4\ \ text(… as required)`

 

v.   `text(S)text(ince)\ \ v^2=(5d)/(F(theta)),`

`=>\ v^2\ \ text(is a MIN when)\ \  F(theta)\ \ text(is a MAX)`

`text(We know)\ \ F prime(theta)=0\ \ text(when)\ \ theta=alpha/2+pi/4`

♦♦♦ Mean mark 9%
MARKER’S COMMENT: Only a small minority of students  explained correctly that  `v^2`  is a MIN when  `F(theta)`  is a MAX.

`:.\ text(MAX or MIN when)\ \ theta=alpha/2+pi/4`

 

`F prime(theta)=cos 2theta+sin 2theta tan alpha`

`F ″(theta)=-2sin2theta+2cos2theta tan alpha`

`text(When)\ \ theta=alpha/2+pi/4`

`F″(alpha/2+pi/4)=-2sin(alpha+pi/2)+2cos(alpha+pi/2)tan alpha`

`text(S)text(ince)\ \ 0<alpha<pi/2`

`=> tan alpha>0`

`=>sin(alpha+pi/2)>0`

`=>cos(alpha+pi/2)<0`

`:. F″(alpha/2+pi/4)<0\ \ text(i.e.  MAX)`

`:.\ v^2\ \ text(is a minimum.)`  

Mechanics, EXT2* M1 2011 HSC 6b

The diagram shows the trajectory of a ball thrown horizontally, at speed `v` m/s, from the top of a tower `h` metres above the ground level.
 

2011 6b
 

The ball strikes the ground at an angle of  45°, `d` metres from the base of the tower, as shown in the diagram. The equations describing the trajectory of the ball are

`x=vt`   and   `y=h-1/2 g t^2`,    (DO NOT prove this)

where `g` is the acceleration due to gravity, and `t` is time in seconds.

  1. Prove that the ball strikes the ground at time  
     
         `t=sqrt((2h)/(g))`  seconds.    (1 mark)

  2. Hence, or otherwise, show that  `d=2h`.    (2 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}` 
  2. `text{Proof  (See Worked Solutions)}`
Show Worked Solution

i.   `text(Show)\ \ y=0\ \ text(when)\ t=sqrt((2h)/g)\ \ text(seconds:)`

`0` `=h-1/2 g t^2`
`1/2 g t^2` `=h`
`t^2` `=(2h)/g`
`:.t` `=sqrt((2h)/g)\ \ text(seconds,)\ \ t>=0\ \ text(… as required)`

 

ii.   `text(Show that)\ d=2h`

`x=vt\ \ \ \ =>\ \ \ dotx=v`

`y=h-1/2 g t^2\ \ \ \ =>\ \ \ doty=-g t`

`text(At)\ t=sqrt((2h)/g)`,

`doty` `=-gxxsqrt((2h)/g)`
  `=-sqrt(2gh)`

 

`text(S)text(ince the ball strikes the ground at)\ 45^@,\ text(we know)`

♦♦ Mean mark 33%
STRATEGY: The key to unlocking this proof is understanding that `tan theta`, where  `theta` is the angle of trajectory at impact of a projectile, equals  `|\ doty\ |/dotx`.
`tan45^@=` `|\ doty\ |/dotx`
`1=` `sqrt(2gh)/v`
`v=` `sqrt(2gh)`

 
`text(S)text(ince)\ \ x=d=vt\ \ text(when)\ \ t=sqrt((2h)/g)`

`d` `=sqrt(2gh)xxsqrt((2h)/g)`
  `=sqrt((2h)^2)`
  `=2h\ \ text( … as required)`

Mechanics, EXT2* M1 2013 HSC 13c

Points `A` and `B` are located `d` metres apart on a horizontal plane. A projectile is fired from `A` towards `B` with initial velocity `u` m/s at angle `alpha` to the horizontal.

At the same time, another projectile is fired from `B` towards `A` with initial velocity `w` m/s at angle `beta` to the horizontal, as shown on the diagram.

The projectiles collide when they both reach their maximum height.
 

2013 13c
 

The equations of motion of a projectile fired from the origin with initial velocity  `V` m/s at angle  `theta`  to the horizontal are

`x=Vtcostheta`   and   `y=Vtsintheta-g/2 t^2`.        (DO NOT prove this.)

  1. How long does the projectile fired from  `A`  take to reach its maximum height?  (2 marks)

  2. Show that  `usinalpha=w sin beta`.    (1 mark)

  3. Show that  `d=(uw)/(g)sin(alpha+beta)`.    (2 marks)

Show Answers Only
  1. `(u)/(g) sin alpha\ \ text(seconds)`
  2. `text{Proof  (See Worked Solutions)}`
  3. `text{Proof  (See Worked Solutions)}`
Show Worked Solution

i.   `y=Vtsintheta-g/2 t^2`

`text(Projectile)\ A\   => V=u,\ \ theta=alpha`

`y` `=ut sinalpha- (g)/2 t^2`
`doty` `=u sinalpha- g t`

 

`text(Max height when)\  doty=0`

`0` `=usinalpha-g t`
`g t` `=usinalpha`
`t` `=(u)/(g)sinalpha`

 
`:.\ text(Projectile from)\ A\ text(reaches max height at)`

 `t=(u)/(g)sin alpha\ \ text(seconds)`

 

ii.  `text(Show that)\ \ usin alpha=wsin beta`

IMPORTANT: Part (i) in this example leads students to a very quick solution. Always look to previous parts for clues to direct your strategy.

`text(Projectile)\ B\ =>V=w,\ \ theta=beta`

`y` `=wt sin beta- (g)/2 t^2`
`doty` `=wsin beta-g t`

 

`text(Max height when)\ \ doty=0`

`t=(w)/(g) sin beta`

`text{Projectiles collide at max heights}`

`text(S)text(ince they were fired at the same time)`

`(u)/(g) sin alpha` `=(w)/(g) sin beta`
`:.\ usin alpha` `=wsin beta\ \ text(… as required)`

 

iii  `text(Show)\ \ d=(uw)/(g) sin (alpha+beta) :`

`text(Find)\ x text(-values for each projectile at max height)`

`text(Projectile)\ A`

`x_1` `=utcos alpha`
  `=u((u)/(g) sin alpha)cos alpha`
  `=(u^2)/(g) sin alpha cos alpha`

 

`text(Projectile)\ B`

♦ Mean mark 39%
IMPORTANT: Students should direct their calculations by reverse engineering the required result. `sin(alpha+beta)` in the proof means that  `sin alpha cos beta+“ cos alpha sin beta`  will appear in the working calculations.
`x_2` `=wt cos beta`
  `=w((w)/(g) sin beta)cos beta`
  `=(w^2)/(g) sin beta cos beta`
`d` `=x_1+x_2`
  `=(u^2)/(g) sin alpha cos alpha+(w^2)/(g) sin beta cos beta`
  `=(u)/(g)(u sin alpha)cos alpha+(w)/(g) (w sin beta) cos beta`
  `=(u)/(g)(w sin beta) cos alpha+(w)/(g) (usin alpha)cos beta\ \ text{(part (ii))}`
  `=(uw)/(g) (sin alpha cos beta+cos alpha sin beta)`
  `=(uw)/(g) sin (alpha+beta)\ \ text(… as required)`

 

Calculus, 2ADV C4 2009 HSC 7a

The acceleration of a particle is given by

`a=8e^(-2t)+3e^(-t)`,

where  `x`  is the displacement in metres and  `t`  is the time in seconds.

Initially its velocity is  `text(– 6 ms)^(–1)` and its displacement is 5 m.

  1. Show that the displacement of the particle is given by
  2. `qquad  x=2e^(-2t)+3e^-t+t`.   (2 marks) 

  3. Find the time when the particle comes to rest.    (3 marks)

  4. Find the displacement  when the particle comes to rest.    (1 mark)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `ln4\ text(seconds)`
  3. `7/8+ln4\ \ text(units)`
Show Worked Solution

i.    `text(Show)\ \ x=2e^(-2t)+3e^-t+t`

`a=8e^(-2t)+3e^-t\ \ text{(given)}`

`v=int a\ dt=-4e^(-2t)-3e^-t+c_1`

`text(When)\ t=0,  v=-6\ \ text{(given)}`

`-6` `=-4e^0-3e^0+c_1`
`-6` `=-7+c_1`
`c_1` `=1`

 
`:. v=-4e^(-2t)-3e^-t+1`
 

`x` `=int v\ dt`
  `=int(-4e^(-2t)-3e^-t+1)\ dt`
  `=2e^(-2t)+3e^-t+t+c_2`

 
`text(When)\ \ t=0,\ x=5\ \ text{(given)}`

`5` `=2e^0+3e^0+c_2`
`c_2` `=0`

 
`:.\ x=2e^(-2t)+3e^-t+t\ \ text(… as required)`

 

ii.   `text(Particle comes to rest when)\ \ v=0`

`text(i.e.)\ \ -4e^(-2t)-3e^-t+1=0`

`text(Let)\ X=e^-t\ \ \ \ =>X^2=e^(-2t)`

`-4X^2-3X+1` `=0`
`4X^2+3X-1` `=0`
`(4X-1)(X+1)` `=0`

 
 `:.\ \ X=1/4\ \ text(or)\ \ X=-1`

`text(When)\ \ X=1/4:`

`e^-t` `=1/4`
`lne^-t` `=ln(1/4)`
`-t` `=ln(1/4)`
`t` `=-ln(1/4)=ln(1/4)^-1=ln4`

 
`text(When)\ \ X=-1:`

`e^-t=-1\ \ text{(no solution)}`
 

`:.\ text(The particle comes to rest when)\ t=ln4\ text(seconds)`
  

iii.  `text(Find)\ \ x\ \ text(when)\ \ t=ln4 :`

`x=2e^(-2t)+3e^-t+t`

`\ \ =2e^(-2ln4)+3e^-ln4+ln4`

`\ \ =2(e^ln4)^-2+3(e^ln4)^-1+ln4`

`\ \ =2xx4^-2+3xx4^-1+ln4`

`\ \ =2/16+3/4+ln4`

`\ \ =7/8+ln4`

ALGEBRA TIP: Helpful identity  `e^lnx=x`. Easily provable as follows:
`e^ln2=x`
`\ =>lne^ln2=lnx\ `
`\ => ln2=lnx\ `
`\ =>x=2`.

Calculus, EXT1* C1 2010 HSC 7a

The acceleration of a particle is given by

`ddotx=4cos2t`,

where  `x`  is the displacement in metres and  `t`  is the time in seconds. 

Initially the particle is at the origin with a velocity of  `text(1 ms)^(–1)`.

  1. Show that the velocity of the particle is given by

     

      `dotx=2sin2t+1`.    (2 marks)

  2. Find the time when the particle first comes to rest.    (2 marks)

  3. Find the displacement,  `x`,  of the particle in terms of  `t`.    (2 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `(7pi)/12\ text(seconds)`
  3. `x=1-cos2t+t`
Show Worked Solution
i.   `text(Show)\ dotx` `=2sin2t+1`
`dotx` `=intddotx\ dt`
  `=int4cos2t\ dt`
  `=2sin2t+c`

 
`text(When)\ t=0, \ \ dotx=1\ \ text{(given)}`

`1=2sin0+c`

`c=1`

 
`:. dotx=2sin2t+1 \ \ \ text(… as required)`
 

ii.   `text(Find)\ t\ text(when)\ dotx=0 :`

`2sin2t+1` `=0`
`sin2t` `=-1/2`

 
`=>sin theta=1/2\ text(when)\ theta=pi/6`

`text(S)text(ince)\ \ sin theta\ \ text(is negative in 3rd and 4th quadrants)`

`2t` `=pi + pi/6`
`2t` `=(7pi)/6`
`t` `=(7pi)/12`

 
`:.\ text(Particle first comes to rest at)\ t=(7pi)/12\ text(seconds)`
 

iii.    `x` `=intdotx\ dt`
  `=int(2sin2t+1)\ dt`
  `=t-cos2t+c`

 
`text(When)\ t=0,\ x=0\ \ text{(given)}`

`0=0-cos0+c`

`c=1`

 
`:. x=t-cos2t+1`

Calculus, 2ADV C4 2012 HSC 15b

The velocity of a particle is given by

`v=1-2cost`,

where  `x`  is the displacement in metres and  `t`  is the time in seconds. Initially the particle is 3 m to the right of the origin.

  1. Find the initial velocity of the particle.    (1 mark)

  2. Find the maximum velocity of the particle.    (1 mark)

  3. Find the displacement, `x`,  of the particle in terms of  `t`.    (2 marks)

  4. Find the position of the particle when it is at rest for the first time.    (2 marks)

Show Answers Only
  1. `-1\ text(m/s)`
  2. `3\ text(m/s)`
  3. `x=t-2sint+3`
  4. `pi/3-sqrt3+3`
Show Worked Solution

i.    `text(Find)\ \ v\ \ text(when)\ \ t=0`:

`v` `=1-2cos0`
  `=1-2`
  `=-1`

 
`:.\ text(Initial velocity is)\ -1\ text(m/s.)`

 

ii.  `text(Solution 1)`

`text(Max velocity occurs when)\ \ a=(d v)/(dt)=0`

♦♦ Mean mark 29%
MARKER’S COMMENT: Solution 2 is more efficient here. Using the -1 and +1 limits of trig functions can be very a effective way to calculate max/min values.

`a=2sint`
 

`text(Find)\ \ t\ \ text(when)\ \ a=0 :`

`2sint=0`

`t=0`,  `pi`,  `2pi`, …

`text(At)\ \ t=0,\ \   v=-1\ text(m/s)`

`text(At)\ \ t=pi,\ \ v=1-2(-1)=3\ text(m/s)`

 
`:.\ text(Maximum velocity is 3 m/s)`

 

`text(Solution 2)`

`v=1-2cost`

`text(S)text(ince)\ \ -1` `<cost<1`
`-2` `<2cost<2`
`-1` `<1-2cost<3`

 
`:.\ text(Maximum velocity is 3 m/s)`

 

iii.   `x` `=int v\ dt`
  `=int(1-2cost)\ dt`
  `=t-2sint+c`

 
`text(When)\ \ t=0,\ \ x=3\ \ text{(given)}`

`3=0-2sin0+3`

`c=3`

 
`:. x=t-2sint+3`

 

iv.  `text(Find)\ \ x\ \ text(when)\ \ v=0\ \ text{(first time):}`

♦ Mean mark 50%
MARKER’S COMMENT: Many students found  `t=pi/3`  but failed to gain full marks by omitting to find  `x`. Remember that for calculus, angles are measured in radians, NOT degrees!

`text(When)\ \ v=0 ,`

`0` `=1-2cost`
`cost` `=1/2`
`t` `=cos^-1(1/2)`
  `=pi/3\ \ \ text{(first time)}`

 
`text(Find)\ \ x\ \ text(when)\ \ t=pi/3 :`

`x` `=pi/3-2sin(pi/3)+3`
  `=pi/3-2xxsqrt3/2+3`
  `=pi/3-sqrt3+3\ \ text(units)`

Calculus, 2ADV C3 2012 HSC 16b

The diagram shows a point  `T`  on the unit circle  `x^2+y^2=1`  at an angle  `theta`  from the positive  `x`-axis, where  `0<theta<pi/2`.

The tangent to the circle at  `T`  is perpendicular to  `OT`, and intersects the  `x`-axis at  `P`,  and the line  `y=1`  intersects the  `y`-axis at  `B`.
 

 
 

  1. Show that the equation of the line  `PT`  is  `xcostheta+ysin theta=1`.    (2 marks)

  2. Find the length of  `BQ`  in terms of  `theta`.    (1 mark)

  3. Show that the area,  `A`,  of the trapezium  `OPQB`  is given by 
     
         `A=(2-sintheta)/(2costheta)`    (2 marks)

  4. Find the angle  `theta`  that gives the minimum area of the trapezium.    (3 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `(1-sin theta)/cos theta`
  3. `text{Proof  (See Worked Solutions)}`
  4. `theta=pi/6\ \ text(radians)`
Show Worked Solution
i.    

`text(Find)\  T:`

♦♦ Mean mark 20%

`text(S)text(ince)\ \ cos theta=x/1\ \ \ text(and)\ \ \  sin theta=y/1`

`:. T\ (cos theta, sin theta)`

`text(Gradient of)\ OT=sin theta/cos theta`

`:.\ text(Gradient)\ PT=-cos theta/sin theta\ \ text{(} _|_ text{lines)}`

`text(Equation of)\ PT\ text(where)`

`m=-cos theta/sin theta,\ \ text(and through)\ \ (cos theta, sin theta)`

`text(Using)\ \ y-y_1` `=m(x-x_1)`
`y-sin theta` `=-cos theta/sin theta(x-cos theta)`
`y sin theta-sin^2 theta` `=-x cos theta+cos^2 theta`
`x cos theta+y sin theta` `=sin^2 theta+cos^2 theta`
`x cos theta+y sin theta` `=1\ \ \ \ \ text(… as required)`

 

ii.   `text(Find)\ Q:`

 `Q\ => text(intersection of)\ xcos theta+y sin theta=1\ \ text(and)\ \ y=1`

`x cos theta+sin theta` `=1`
`x cos theta` `=1-sin theta`
`x` `=(1-sin theta)/cos theta`

 
`:.\ text(Length of)\ BQ\ text(is)\ \ (1-sin theta)/cos theta\ text(units)`

 

iii.  `text(Show Area)\ OPQB=(2-sin theta)/(2cos theta)`

`A=1/2h(a+b)\ \ text(where)\ \ h=OB=1\ \   a=OP\ \  text(and)`  

                `b=BQ=(1-sin theta)/cos theta`

`text(Find  length)\ OP:`

`P => xcos theta+ysin theta=1 \ text(cuts)\ \ x text(-axis)`

♦♦ Mean mark 24%
`xcos theta` `=1`
`x` `=1/cos theta`
`=>text(Length)\ OP` `=1/cos theta`

 

`text(Area)\ OPQB` `=1/2xx1(1/cos theta+(1-sin theta)/cos theta)`
  `=1/2((2-sin theta)/cos theta)`
  `=(2-sin theta)/(2cos theta)\ \ text(u²)\ \ \ text(… as required)`

 

iv.  `text(Find)\ theta\ text(such that Area)\ OPQB\ text(is a MIN)`

`A` `=(2-sin theta)/(2cos theta)`
`(dA)/(d theta)` `=(2cos theta(-cos theta)-(2- sin theta)(-2 sin theta))/(4cos^2 theta)`
  `=(4 sin theta-2sin^2 theta-2 cos^2 theta)/(4 cos^2 theta)`
  `=(4sin theta-2(sin^2 theta+cos^2 theta))/(4 cos^2 theta)`
  `=(4sin theta-2)/(4cos^2 theta)`
  `=(2sin theta-1)/(2 cos^2 theta)`
Mean mark 19%
IMPORTANT: Look for any opportunity to use the identity `sin^2 theta“+cos^2 theta=1` → often a key to simplifying difficult trig equations.
 

`text(MAX or MIN when)\ (dA)/(d theta)=0`

`=>2sin theta-1` `=0`
`sin theta` `=1/2`
`theta` `=pi/6\ \ \ \ \0<theta<pi/2` 

 
`text(Test for MAX/MIN)`

IMPORTANT: Is the 1st or 2nd derivative test easier here? Examiners have often made one significantly easier than the other.

`text(If)\ theta=pi/12\ \ (dA)/(d theta)<0`

`text(If)\ theta=pi/3\ \ (dA)/(d theta)>0\ \ =>text(MIN)`

`:.\text(Area)\ OPQB\ text(is a MIN when)\ theta=pi/6`.

Calculus, 2ADV C3 2013 HSC 14b

Two straight roads meet at  `R`  at an angle of 60°.  At time  `t=0`  car  `A`  leaves  `R`  on one road, and car  `B`  is 100km from  `R`  on the other road.  Car  `A`  travels away from  `R`  at a speed of 80 km/h, and car  `B`  travels towards  `R`  at a speed of 50 km/h.
 

2013 14b

The distance between the cars at time  `t`  hours is  `r`  km.

  1. Show that  `r^2=12\ 900t^2-18\ 000t+10\ 000`.   (2 marks)

  2. Find the minimum distance between the cars.    (3 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `61\ text(km)`
Show Worked Solution

i.   `text(Need to show)\  r^2=12\ 900t^2-18\ 000t+10\ 000`

♦♦ Mean mark 26%

`RB=100-50t`

`RA=80t`

`text(Using the cosine rule)`

`r^2` `=(RB)^2+(RA)^2-2(RB)(RA)cos/_R`
  `=(100-50t)^2+(80t)^2-2(100-50t)(80t)cos60`
  `=10\ 000-10\ 000t+2500t^2+6400t^2-8000t+4000t^2`
  `=12\ 900t^2-18\ 000t+10\ 000\ \ \ \ text(… as required)` 

 

ii.   `text(Max/min when)\ (dr^2)/(dt)=0`

♦♦ Mean mark 27%
ALGEBRA TIP: Finding the derivative of `r^2` (rather than making `r` the subject), makes calculations much easier. ENSURE you apply the test to confirm a minimum.

`(dr^2)/(dt)=25\ 800t-18\ 000=0`

`t=(18\ 000)/(25\ 800)=30/43`

`text(When)\  t=30/43,\   (d^2(r^2))/(dt^2)=25\ 800>0\ \ =>text(MIN)`

`:.\ text(Minimum distance when)\  t=30/43\ text(hr)`

`text(Find)\  r\ text(when)\ t=30/43`

`r^2` `=12\ 900(30/43)^2-18\ 000(30/43)+10\ 000`
  `=3720.9302…`
`:.\ r` `=sqrt3702.9302…`
  `~~60.99942…`
  `~~61\ text{km  (nearest km)}`

 

`:.\ text(MIN distance between the cars is 61 km.)`

Calculus, EXT1* C1 2008 HSC 5c

Light intensity is measured in lux. The light intensity at the surface of a lake is 6000 lux. The light intensity,  `I`  lux, a distance  `s`  metres below the surface of the lake is given by

`I=Ae^(-ks)`

where  `A`,  and  `k`  are constants.

  1. Write down the value of  `A`.   (2 marks)

  2. The light intensity 6 metres below the surface of the lake is 1000 lux. Find the value of  `k`.    (2 marks)

  3. At what rate, in lux per metre, is the light intensity decreasing 6 metres below the surface of the lake?    (2 marks)

Show Answers Only
  1. `6000`
  2. `- 1/6 ln(1/6)\ text(or)\ 0.29863`
  3. `299`
Show Worked Solution

i.   `I=Ae^(-ks)`

`text(Find)\ A,\ text(given)\   I=6000\ text(at)\  s=0`

`6000` `=Ae^0`
`:.\ A` `=6000`

 

ii.   `text(Find)\ k\ text(given)\  I=1000\ text(at)  s=6`

MARKER’S COMMENT: Many students used the “log” function on their calculator rather than the `log_e` function. BE CAREFUL!
`1000` `=6000e^(-6xxk)`
`e^(-6k)` `=1/6`
`lne^(-6k)` `=ln(1/6)`
`-6k` `=ln(1/6)`
`k` `=- 1/6 ln(1/6)`
  `=0.2986…`
  `=0.30\ \ \ text{(2 d.p.)}`

 

iii.  `text(Find)\ \ (dI)/(ds)\ \ text(at)\ \ s=6`

ALGEBRA TIP: Tidy your working by calculating `(dI)/(ds)` using `k` and then only substituting for `k` in part (ii) at the final stage.
`I` `=6000e^(-ks)`
`:.(dI)/(ds)` `=-6000ke^(-ks)`

 
`text(At)\ s=6,`

`(dI)/(ds)` `=-6000ke^(-6k),\ \ \ text(where)\ k=- 1/6 ln(1/6)`
  `=-298.623…`
  `=-299\ \ text{(nearest whole number)}`

 
`:. text(At)\ s=6,\ text(the light intensity is decreasing)`

`text(at 299 lux per metre.)`

Calculus, EXT1* C1 2009 HSC 6b

Radium decays at a rate proportional to the amount of radium present. That is, if  `Q(t)`  is the amount of radium present at time  `t`,  then  `Q=Ae^(-kt)`,  where  `k`  is a positive constant and  `A`  is the amount present at  `t=0`. It takes 1600 years for an amount of radium to reduce by half.

  1. Find the value of  `k`.   (2 marks)

  2. A factory site is contaminated with radium. The amount of radium on site is currently three times the safe level.

     

    How many years will it be before the amount of radium reaches the safe level.    (2 marks)

Show Answers Only
  1. `(-ln(1/2))/1600\ \ text(or 0.000433)`
  2. `2536\ text(years)`
Show Worked Solution

i.   `Q=Ae^(-kt)`

MARKER’S COMMENT: Students must be familiar with “half-life” and the algebra required. i.e. using `Q=1/2 A` within their calculations.

`text(When)\ \ t=0,\ \ Q=A`

`text(When)\ \ t=1600,\ \ Q=1/2 A`

`:.1/2 A` `=A e^(-1600xxk)`
`e^(-1600xxk)` `=1/2`
`lne^(-1600xxk)` `=ln(1/2)`
`-1600k` `=ln(1/2)`
`k` `=(-ln(1/2))/1600`
  `=0.0004332\ \ text{(to 4 sig. figures)}`

 

ii.   `text(Find)\ \ t\ \ text(when)\ \ Q=1/3 A :`

IMPORTANT: Know how to use the memory function on your calculator to store the exact value of `k` found in part (i) to save time.
`1/3 A` `=A e^(-kt)`
`e^(-kt)` `=1/3`
`lne^(-kt)` `=ln(1/3)`
`-kt` `=ln(1/3)`
`:.t` `=(-ln(1/3))/k,\ \ \ text(where)\ \ \ k=(-ln(1/2))/1600`
  `=(ln(1/3) xx1600)/ln(1/2)`
  `=2535.940…`

 
`:.\ text(It will take  2536  years.)`

Calculus, EXT1* C1 2011 HSC 10a

The intensity, `I`,  measured in  watt/m2,  of a sound is given by

`I=10^-12xxe^(0.1L)`,

where  `L`  is the loudness of the sound in decibels.

  1. If the loudness of a sound at a concert is 110 decibels, find the intensity of the sound. Give your answer in scientific notation.   (1 mark)

  2. Ear damage occurs if the intensity of a sound is greater than `8.1xx10^-9`  watt/m2.

     

    What is the maximum loudness of a sound so that no ear damage occurs?    (2 marks)

  3. By how much will the loudness of a sound have increased if its intensity has doubled?     (2 marks)

Show Answers Only
  1. `6xx10^-8\ \ text{(1 sig. figure)}`
  2. `90\ text(decibels)`
  3. `7\ text(decibels)`
Show Worked Solution

i.    `text(Find)\ I\ text(when)\ \ L=110`

MARKER’S COMMENT: Note that `e^11 xx 10^-12` is not correct scientific notation.
`I` `=10^-12xxe^(0.1xx110)`
  `=10^-12xxe^11`
  `=5.9874…\ \ xx10^-8`
  `=6xx10^-8\ \ \ text{(to 1 sig. fig.)}`

 

ii.   `text(Find)\ \ L\ \ text(such that)\ \ \ I=8.1xx10^-9`

`text(i.e.)\ \ \  8.1xx10^-9` `=10^-12xxe^(0.1L)`
`e^(0.1L)` `=8.1xx10^3`
`lne^(0.1L)` `=ln8100`
`0.1L xx ln e` `=ln8100`
`L` `=ln8100/0.1`
  `=89.996…`
  `=90\ \ text{(nearest whole)}`

 
`:.\ 90\ text(decibels is the maximum loudness.)`

 

iii.  `text(Let)\ \ I=I_0 e^(0.1L)`

♦♦ Mean mark 32%
MARKER’S COMMENT: Actual values can help here. Calculate the intensity at `L=0` (which equals `1xx10^-12`) and then find `L` when this intensity level is doubled (to `2xx10^-12`).

`text(Find)\ \ L\ \ text(when)\ \ I=2I_0`

`2I_0` `=I_0e^(0.1L)`
`e^(0.1L)` `=2`
`lne^(0.1L)` `=ln2`
`0.1L` `=ln2`
`L` `=ln2/0.1`
  `=6.93147…`
  `=7\ \ text{(nearest whole)}`

 
`:.\ text(The loudness of a sound must increase 7)`

`text(decibels for the intensity to double.)`

Calculus, EXT1* C1 2013 HSC 16b

Trout and carp are types of fish. A lake contains a number of trout. At a certain time, 10 carp are introduced into the lake and start eating the trout. As a consequence, the number of trout,  `N`,  decreases according to

`N=375-e^(0.04t)`,

where `t` is the time in months after the carp are introduced.

The population of carp,  `P`,  increases according to  `(dP)/(dt)=0.02P`.

  1. How many trout were in the lake when the carp were introduced?    (1 mark)

  2. When will the population of trout be zero?    (1 mark)

  3. Sketch the number of trout as a function of time.     (1 marks)

  4. When is the rate of increase of carp equal to the rate of decrease of trout?    (3 marks)

  5. When is the number of carp equal to the number of trout?    (2 marks)

Show Answers Only
  1. `text(374 trout)`
  2. `text{148 months (nearest month)}`
  3.  
     
    2UA 2013 HSC 16b Answer
  4. `text{After 80 months (nearest month)}`
  5. `text{After 135 months (nearest month)}`
Show Worked Solution

i.    `text(Carp introduced at)\ \ t=0`

MARKER’S COMMENT: A number of students did not equate `e^0=1` in this part.

`N=375-e^0=374`

`:.\ text(There was 374 trout when carp were introduced.)`

 

ii.    `text(Trout population will be zero when)`

NOTE: The last line of the solution isn’t necessary but is included as good practice as a check that the answer matches the exact question asked.
`N` `=375-e^(0.04t)=0`
`e^(0.04t)` `=375`
`0.04t` `=ln375`
`t` `=ln375/0.04`
  `=148.173 …`
  `=148\ text{months (nearest month)}`

 
`:.\ text(After 148 months, the trout population will be zero.)`
 

iii.   2UA 2013 HSC 16b Answer

♦♦ Mean mark 33% for part (iii)

 

iv.   `text(We need) \ |(dN)/(dt)|=(dP)/(dt)`

`text(Given)\ N=375-e^(0.04t)`

`(dN)/(dt)=-0.04e^(0.04t)`
  

`text(Find)\ P\ text(in terms of)\  t`

`text(Given)\ (dP)/(dt)=0.02P`

`=> P=Ae^(0.02t)`

♦♦♦ Mean mark 20%
COMMENT: Students who progressed to `0.2e^(0.02t)“=0.04e^(0.04t)` received 2 full marks in this part. Show your working!

 `text(Find)\ A\ \ =>text(when)\  t=0,\ P=10`

`10` `=Ae^0`
`:.A` `=10`
`=>(dP)(dt)` `=10xx0.02e^(0.02t)`
  `=0.2e^(0.02t)`

 
`text(Given that)\ \ (dP)/(dt)=|(dN)/(dt)|`

`0.2e^(0.02t)` `=0.04e^(0.04t)`
`5e^(0.02t)` `=e^(0.04t)`
`e^(0.04t)/e^(0.02t)` `=5`
`e^(0.04t-0.02t)` `=5`
`lne^(0.02t)` `=ln5`
`0.02t` `=ln5`
`t` `=ln5/0.02`
  `=80.4719…`
  `=80\ text{months (nearest month)}`

 

v.   `text(Find)\ t\ text(when)\ N=P`

`text(i.e.)\ \ 375-e^(0.04t)` `=10e^(0.02t)`
`e^(0.04t)+10e^(0.02t)-375` `=0`

`text(Let)\ X=e^(0.02t),\ text(noting)\ \ X^2=(e^(0.02t))^2=e^(0.04t)`

♦♦♦ Mean mark 4%!
MARKER’S COMMENT: Correctly applying substitution to exponentials to form a solvable quadratic proved very difficult for almost all students.
`:.\ X^2+10X-375` `=0`
`(X-15)(X+25)` `=0`

`X=15\ \ text(or)\ \ –25`

 
`text(S)text(ince)\  X=e^(0.02t)`

`e^(0.02t)` `=15\ \ \ \ (e^(0.02t)>0)`
`lne^(0.02t)` `=ln15`
`0.02t` `=ln15`
`t` `=ln15/0.02`
  `=135.4025…`
  `=135\ text(months)`

Calculus, 2ADV C3 2011 HSC 7b

The velocity of a particle moving along the `x`-axis is given by

`v=8-8e^(-2t)`,

where `t` is the time in seconds and `x` is the displacement in metres.

  1. Show that the particle is initially at rest.     (1 mark)

  2. Show that the acceleration of the particle is always positive.     (1 mark)

  3. Explain why the particle is moving in the positive direction for all  `t>0`.     (2 marks)

  4. As  `t->oo`, the velocity of the particle approaches a constant.

     

    Find the value of this constant.     (1 mark) 

  5. Sketch the graph of the particle's velocity as a function of time.     (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `text{Proof (See Worked Solutions)}`
  3. `text(See Worked Solutions.)`
  4. `8\ text(m/s)`
  5. `text(See sketch in Worked Solutions)`
Show Worked Solution

i.   `text(Initial velocity when)\ \ t=0`

`v` `=8-8e^0`
  `=0\ text(m/s)`
 
`:.\ text(Particle is initially at rest.)`

 

 

MARKER’S COMMENT: Students whose working showed `e^(-2t)` as `1/e^(2t)`, tended to score highly in this question.

ii.   `a=d/(dt) (v)=-2xx-8e^(-2t)=16e^(-2t)`

`text(S)text(ince)\  e^(-2t)=1/e^(2t)>0\ text(for all)\  t`.

`=>\ a=16e^(-2t)=16/e^(2t)>0\ text(for all)\  t`.
 

`:.\ text(Acceleration is positive for all)\ \ t>0`.
 

iii.  `text{S}text{ince the particle is initially at rest, and ALWAYS}`

♦♦♦ Mean mark 22%
COMMENT: Students found part (iii) the most challenging part of this question by far.

`text{has a positive acceleration.`
 

`:.\ text(It moves in a positive direction for all)\ t`.
 

iv.   `text(As)\ t->oo`,  `e^(-2t)=1/e^(2t)->0`

`=>8/e^(2t)->0\  text(and)`

`=>v=8-8/e^(2t)->8\ text(m/s)`
 

`:.\ text(As)\ \ t->oo,\ text(velocity approaches 8 m/s.)`

 

IMPORTANT: Use previous parts to inform this diagram. i.e. clearly show velocity was zero at  `t=0`  and the asymptote at  `v=8`. 
v.   

Calculus in the Physical World, 2UA 2011 HSC 7b Answer

Calculus, 2ADV C4 2010 HSC 5c

The diagram shows the curve  `y=1/x`, for  `x>0`.

The area under the curve between  `x=a`  and  `x=1`  is  `A_1`. The area under the curve between  `x=1`  and  `x=b`  is  `A_2`.
 

2010 5c
 

The areas  `A_1`  and  `A_2`  are each equal to `1` square unit.

Find the values of  `a`  and  `b`.     (3 marks)

Show Answer Only

`a=1/e`

`b=e`

Show Worked Solutions
IMPORTANT: Note when `log_e a=1`, the definition of a log means that `e^1=a`. Many students failed to earn an easy 3rd mark by recognising this.
`int_a^1 1/x \ dx` `=1`
`[ln x]_a^1` `=1`
`ln1-lna` `=1`
`lna` `=-1`
`:.\ a` `=e^-1=1/e`

 

`int_1^b 1/x dx` `=1`
`[lnx]_1^b` `=1`
`lnb-ln1` `=1`
`ln b` `=1`
`:.b` `=e`

Financial Maths, 2ADV M1 2008 HSC 9b

Peter retires with a lump sum of $100 000. The money is invested in a fund which pays interest each month at a rate of 6% per annum, and Peter receives a fixed monthly payment `$M` from the fund. Thus the amount left in the fund after the first monthly payment is   `$(100\ 500-M)`.

  1. Find a formula for the amount, `$A_n`, left in the fund after `n\ ` monthly payments.   (2 marks)

  2. Peter chooses the value of `M` so that there will be nothing left in the fund at the end of the 12th year (after 144 payments). Find the value of `M`.   (3 marks)

Show Answers Only
  1.  `100\ 000(1.005^n)-M((1.005^n-1)/0.005)`
  2. `$975.85`
Show Worked Solutions

i.    `r=(1+0.06/12)=1.005`

MARKER’S COMMENT: Students who developed this answer from writing the calculations of `A_1`, `A_2`, `A_3` to then generalising for `A_n` were the most successful.
`A_1` `=(100\ 500-M)`
  `=100\ 000(1.005)^1-M`
`A_2` `=A_1 (1.005)-M`
  `=[100\ 000(1.005^1)-M](1.005)-M`
  `=100\ 000(1.005^2)-M(1.005)-M`
  `=100\ 000(1.005^2)-M(1+1.005)`
`A_3` `=100\ 000(1.005^3)-M(1+1.005^1+1.005^2)`

`\ \ \ \ \ vdots`

`A_n` `=100\ 000(1.005^n)-M(1+1.005+\ …\ +1.005^(n-1))`
  `=100\ 000(1.005^n)-M((a(r^n-1))/(r-1))`
  `=100\ 000(1.005^n)-M((1(1.005^n-1))/(1.005-1))`
  `=100\ 000(1.005^n)-M((1.005^n-1)/0.005)`

 

ii.  `text(Find)\ M\  text(such that)\ \ $A_n=0\ \ text(when)\ \ n=144`

`A_144=100\ 000(1.005)^144-M((1.005^144-1)/0.005)=0`

`M((1.005^144-1)/0.005)` `=100\ 000(1.005^144)`
`M(1.005^144-1)` `=500(1.005^144)`
`M` `=(500(1.005^144))/(1.005^144-1)`
  `=975.85`

 

`:. M=$975.85\ \ text{(nearest cent).}`

Financial Maths, 2ADV M1 2008 HSC 5b

Consider the geometric series

`5+10x+20x^2+40x^3+\ ...`

  1. For what values of `x` does this series have a limiting sum?    (2 marks)

  2. The limiting sum of this series is `100`.

     

    Find the value of `x`.     (2 marks)

Show Answers Only
  1. `-1/2<x<1/2`
  2. `19/40`
Show Worked Solutions

i.   `text(Limiting sum when)\ |\ r\ |<1`

`r=T_2/T_1=(10x)/5=2x`

`:.\ |\ 2x\ |<1`

`text(If)\ \ 2x` `>0` `text(If)\ \ 2x` `<0`
`2x` `<1` `-(2x)` `<1`
`x` `<1/2` `2x` `> -1`
    `x` `> -1/2`

 

`:. text(Limiting sum when)\ \ -1/2<x<1/2`

 

ii.  `text(Given)\  S_oo=100,  text(find) \ x`

`=> S_oo=a/(1-r)=100`

` 5/(1-2x)` `=100`
`100(1-2x)` `=5`
`200x` `=95`
`:.\ x` `=95/200=19/40`

Calculus, EXT1* C1 2013 HSC 14a

The velocity of a particle moving along the `x`-axis is given by  `dotx=10-2t`, where `x` is the displacement from the origin in metres and `t` is the time in seconds. Initially the particle is 5 metres to the right of the origin.

  1. Show that the acceleration of the particle is constant.  (1 mark)

  2. Find the time when the particle is at rest.  (1 mark)

  3. Show that the position of the particle after 7 seconds is 26 metres to the right of the origin.  (2 marks)

  4. Find the distance travelled by the particle during the first 7 seconds.   (2 marks)

Show Answers Only
  1.  `ddotx=-2\ \ text{(constant)}`
  2. `t=5\ text(seconds)`
  3. `text{Proof (See Worked Solutions)}`
  4. `29\ text(metres)`
Show Worked Solutions

i.   `dotx=10-2t`

`text(Acceleration)=ddotx=d/(dx)dotx=-2`

 
`:.\ text(The acceleration is constant.)`

 

 ii.  `text(Particle comes to rest when)\  dotx=0`

`10-2t=0\ text(when)\ t=5`

 
`:.\ text(Particle comes to rest after 5 seconds.)`

 

 iii. `text(Show)\  x=26\ text(when)\ t=7`

`x` `=int dotx\ dt`
  `=int (10-2t)\ dt`
  `=10t -t^2+c`

 

`text(Given)\  t=0\ text(when)\ x=5`

`=> 5` `=10(0)-0^2+c`
`c` `=5`

 
`:. x=10t-t^2+5`
 

`text(At)\ \ t=7`

`x` `=10(7)-7^2+5`
  `=70-49+5`
  `=26`

 
`:.\ text(The particle is 26 metres to the right of the origin)`

`text(after 7 seconds … as required)`

 

 iv.   `text(Find the distance travelled in the first 7 seconds:)`

♦ Mean mark 37%.
IMPORTANT: Students can also draw a number line that shows where a particle starts from, changes direction and finishes in order to reduce errors.

`text(At)\  t=5`,

`x` `=10(5)-5^2+5`
  `=50-25+5`
  `=30\ text(m)`

 
`=>\ text{The particle travels 25 m to the right}\ (x=5\ text{to}\ 30)`

`text{then 4 m to the left}\  (x=30\ text{to}\ 26)`
 

`:.\ text(The total distance travelled in 7 seconds)`

`=25+4`

`=29\ text(m)`

Proof, EXT2* P2 2009 HSC 7a

  1. Use differentiation from first principles to show that  `d/(dx)(x)=1`.   (1 mark)

  2. Use mathematical induction and the product rule for differentiation to prove that  
     
        `d/(dx)(x^n)=nx^(n-1)`  for all positive integers `n`.   (2 marks)

Show Answer Only
  1. `text{Proof (See Worked Solutions)}`
  2. `text{Proof (See Worked Solutions)}`
Show Worked Solution

i.   `text(Prove)\ \ d/(dx)(x)=1\ \ text(from first principles.)`

MARKER’S COMMENT: Students are reminded to use the number of marks allocated to a question as a guide to the work involved in answering it.
`d/(dx)(x)` `=lim_(h->0) (f(x+h)-f(x))/h`
  `=lim_(h->0)(x+h-x)/h`
  `=1\ \ \ text(… as required)`

 

ii.  `text(Prove)\ \ d/(dx)(x^n)=nx^(n-1)\ \ text(for integers)\ n>=1`

`text(If)\  n=1,`

`text(LHS)=d/(dx)(x^1)=1`

`text(RHS)=(1)x^0=1=text(LHS)`

`:.\ text(True for)\ n=1`

 
`text(Assume true for)\ n=k`

`text(i.e.)\ \ d/(dx)(x^k)=kx^(k-1)`

 `text(Prove true for)\ n=k+1`

IMPORTANT: Critical to read carefully and apply the product rule to prove the induction.

`text(i.e.)\ \ d/(dx)x^(k+1)=(k+1)x^k`

`text(LHS)` `=d/(dx)(x^(k+1))`
  `=d/(dx) (x*x^k)`
  `=d/(dx)(x) * x^k+x *d/(dx)(x^k)`
  `=(1xx x^k)+(x xxkx^(k-1))`
  `=x^k+kx^k`
  `=(k+1)x^k`
  `=\ text(RHS … as required)`

 
`=>\ text(True for)\ n=k+1`

`:.\ text(S)text(ince it is true for)\ n=1, text(by PMI, true for integral)\ n>=1`.

Proof, EXT2* P2 2013 HSC 14a

  1. Show that for  `k>0,\ \ 1/(k+1)^2-1/k+1/(k+1)<0`.    (1 mark)

  2. Use mathematical induction to prove that for all integers  `n>=2`,
     
        `1/1^2+1/2^2+1/3^2+\ …\ +1/n^2<2-1/n`.   (3 marks)

Show Answer Only
  1. `text{Proof (See Worked Solutions)}`
  2. `text{Proof (See Worked Solution)}`
Show Worked Solution

i.  `text(Prove that for)\ k>0,\ \ 1/(k+1)^2-1/k+1/(k+1)<0`

♦♦ Mean mark 25%.
MARKER’S COMMENT: Student algebra was poor in creating a common denominator and justifying why the final expression is always negative proved challenging.
`text(LHS)` `=(k-(k+1)^2+k(k+1))/(k(k+1)^2)`
  `=(k-(k^2+2k+1)+k^2+k)/(k(k+1)^2)`
  `=(-1)/(k(k+1)^2)`

 
`text(S)text(ince)\ \ k>0,\ text(we know)\ \ k(k+1)^2>0`

`:.\ (-1)/(k(k+1)^2)<0\ \ text(… as required)`

 

ii.  `text(Prove)\ \ 1/1^2+1/2^2+1/3^2+\ …\ +1/n^2<2-1/n\ \ text(for integer)\ \ n>=2`

`text(If)\ \ n=2`

`text(LHS)=1/1^2+1/2^2=5/4`

`text(RHS)=2-1/2=3/2 > text(LHS)`

`:.\ text(True for)\ \ n=2`

 
`text(Assume true for)\ \ n=k`

`text(i.e.)\ \ 1/1^2+1/2^2+\ …\ +1/k^2<2-1/k`

 
`text(Prove true for)\ \ n=k+1`

`text(i.e.)\ 1/1^2+1/2^2+\ …\ +1/k^2+1/(k+1)^2<2-1/(k+1)`

♦♦ Mean mark of 26%.
IMPORTANT: Students have to carefully examine part (i) of this question to provide the information required to prove true for `n=k+1`.
`text(LHS)` `=1/1^2+1/2^2+\ …\ +1/k^2+1/(k+1)^2`
  `<2-1/k+1/(k+1)^2`
  `< underbrace{(1/(k+1)^2-1/k+1/(k+1))}_text(<0  from part i)+2-1/(k+1)`
  `<2-1/(k+1)`

  
`=> text(True for)\ n=k+1`

`:.\ text(S)text(ince it is true for)\ n=2, text(by PMI, true for integral)\  n>=2`.

L&E, 2ADV E1 2008 HSC 7a

Solve  `log_e x-3/log_ex=2`   (3 marks)

Show Answers Only

`x=e^3\ \ text(or)\ \ e^-1`

Show Worked Solution
 
IMPORTANT: Students should recognise this equation as a quadratic, and the best responses substituted `log_ex` with a variable such as `X`.
`log_e x-3/(log_ex)` `=2`
`(log_ex)^2-3` `=2log_e x`
`(log_ex)^2-2log_ex-3` `=0`
   
`text(Let)\  X=log_ex`  
`:.\ X^2-2X-3` `=0`
`(X-3)(X+1)` `=0`
MARKER’S COMMENT: Many responses incorrectly stated that there is no solution to `log_ex=-1` or could not find `x` given `log_ex=3`.
`X` `=3` `\ \ \ \ \ \ \ \ \ \ ` `X` `=-1`
`log_ex` `=3` `\ \ \ \ \ \ \ \ \ \ ` `log_ex` `=-1`
`x` `=e^3` `\ \ \ \ \ \ \ \ \ \ ` `x` `=e^-1`

 

`:.x=e^3\ \ text(or)\ \ e^-1`

Financial Maths, 2ADV M1 2009 HSC 8b

One year ago Daniel borrowed $350 000 to buy a house. The interest rate was 9% per annum, compounded monthly. He agreed to repay the loan in 25 years with equal monthly repayments of $2937.

  1. Calculate how much Daniel owed after his first monthly repayment.    (1 mark)

Daniel has just made his 12th monthly repayment. He now owes $346 095. The interest rate now decreases to 6% per annum, compounded monthly.

 

The amount  `$A_n`, owing on the loan after the `n`th monthly repayment is now calculated using the formula  
 
`qquad qquad A_n=346,095xx1.005^n-1.005^(n-1)M-\ ... -1.005M-M`
  
where `$M` is the monthly repayment, and `n=1,2,\ ...,288`.   (DO NOT prove this formula.)

  1. Calculate the monthly repayment if the loan is to be repaid over the remaining 24 years (288 months).    (3 marks)

  2. Daniel chooses to keep his monthly repayments at $2937. Use the formula in part (ii) to calculate how long it will take him to repay the $346 095.   (3 marks)

  3. How much will Daniel save over the term of the loan by keeping his monthly repayments at $2937, rather than reducing his repayments to the amount calculated in part (ii)?   (1 mark)

Show Answers Only
  1. `$349\ 688`
  2. `$2270.31\ \ text{(nearest cent)}`
  3. `178.37\ text(months)`
  4. `$129\ 976.59\ \ text{(nearest cent)}`
Show Worked Solutions

i.   `text(Let)\ L_n= text(the amount owing after)\ n\ text(months)`

`text(Repayment)\ =M=$2937\ \ text(and)\ \ r=text(9%)/12=0.0075\ text(/month)`

`:.\ L_1` `=350\ 000(1+r)-M`
  `=350\ 000(1.0075)-2937`
  `=349\ 688`

 

`:.\ text(After 1 month, the amount owing is)\  $349\ 688`

 

ii.   `text(After 12 repayments, Daniel owes)\ $346\ 095,\  text(and)\ r darr 6%`

`:.\ r=(6%)/12=0.005`

`text(Loan is repaid over the next 24 years. i.e.)\ $A_n=0\ text(when)\  n=288`

`A_n` `=346\ 095(1.005^n)-1.005^(n-1)M-\ ..\ -1.005M-M`
  `=346\ 095(1.005^n)-M(1+1.005+..+1.005^(n-1))`
`A_288` `=346\ 095(1.005^288)-M(1+1.005+..+1.005^287)=0`

`=>\ GP\ text(where)\ a=1,\ text(and)\  r=1.005`

MARKER’S COMMENT: Careless setting out and poor handwriting, especially where indexes were involved, was a major contributor to errors in this question.

`M((1(1.005^288-1))/(1.005-1))=346\ 095(1.005^288)`

`M` `=(1\ 455\ 529.832)/641.1158`
  `=2270.31`

 

`:.\ text{Monthly repayment is $2270.31  (nearest cent)}` 

 

iii.  `text(Given)\ $M\ text(remains at $2937, find)\  n\ text(such that)`

`$A_n=0\ text{(i.e. loan fully paid off)}`

`:. 346\ 095(1.005^n)-2937((1(1.005^n-1))/(1.005-1))` `=0`
`346\ 095(1.005^n)-587\ 400(1.005^n-1)` `=0`
`(346\ 095-587\ 400)(1.005^n)+587\ 400` `=0`
♦♦ A poorly answered question.
MARKER’S COMMENT: Many students struggled to handle the exponential and logarithm calculations in this question.
ALGEBRA TIP: Dividing by `(1.005-1)` in part (iii) is equivalent to multiplying by 200, and cleans up working calculations (see Worked Solutions).
 

`241\ 305(1.005^n)` `=587\ 400`
`ln1.005^n` `=ln((587\ 400)/(241\ 305))`
`n` `=ln2.43426/ln1.005`
  `=178.37..`

 

`:.\ text{He will pay off the loan in 179 months (note the}`

`text{last payment will be a partial payment).}`

 

iv.  `text(Total paid at $2937 per month)`

`= 2937xx178.37=$523\ 872.69`

`text(Total paid at $2270.31 per month)`

`=2270.31xx288=$653,849.28`

 

`:.\ text(The amount saved)`

`=653\ 849.28-523\ 872.69`

`=$129\ 976.59\ \ text{(nearest cent)}`

Financial Maths, 2ADV M1 2010 HSC 9a

  1. When Chris started a new job, $500 was deposited into his superannuation fund at the beginning of each month. The money was invested at 0.5% per month, compounded monthly. 

     

    Let  `$P`  be the value of the investment after 240 months, when Chris retires.

     

    Show that  `P=232\ 175.55`     (2 marks)

  2. After retirement, Chris withdraws $2000 from the account at the end of each month, without making any further deposits. The account continues to earn interest at 0.5% per month.

     

    Let  `$A_n`  be the amount left in the account  `n`  months after Chris's retirement.

     

      (1)  Show that  `A_n=(P-400\ 000)xx1.005^n+400\ 000`.     (3 marks)

     

      (2)  For how many months after retirement will there be money left in the account?     (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. (1)  `text{Proof (See Worked Solutions)}`
  3. (2)  `text(175 months)`
Show Worked Solutions
i.     `P_1` `=500(1.005)`
`P_2` `=500(1.005^2)+500(1.005^1)`
`P_3` `=500(1.005^3+1.005^2+1.005)`
  `vdots`
`P_240` `=500(1.005+1.005^2+1.005^3 …+1.005^240)`

 

`=>\ text(GP where)\ \ a=1.005,\ text(and)\ \ r=1.005`

MARKER’S COMMENT: Common errors included using `r=1.05`, and taking the first term of the GP as 1 instead of 1.005 (note that the $500 goes in at the start of the month and earns interest before it is included in `$P_n`).
`P_240` `=500((a(r^n-1))/(r-1))`
  `=500((1.005(1.005^240-1))/(1.005-1))`
  `=100\ 000[1.005(1.005^240-1)]`
  `=232\ 175.55`

 

`:.\ text(The value of Chris’ investment after 240 months)`

`text(is) \ $232\ 175.55 text(  … as required)`

 

ii. (1)  `text(After 1 month,)\  A_1=P(1.005)-2000`

IMPORTANT: At the end of the month, `$P` earns interest for the month BEFORE any withdrawal is made. Many students mistakenly had `$A_1=(P-2000)(1.005)`.
`A_2` `=A_1(1.005)-2000`
  `=[P(1.005)-2000](1.005)-2000`
  `=P(1.005^2)-2000(1.005)-2000`
  `=P(1.005^2)-2000(1+1.005)`
  ` vdots`
`A_n` `=P(1.005^n)-2000(1+1.005+…+1.005^(n-1))`

`=>\ text(GP where)\ \ a=1\ \ text(and)\ \ r=1.005`

`A_n` `=P(1.005^n)-2000((1(1.005^n-1))/(1.005-1))`
  `=P(1.005^n)-400\ 000(1.005^n-1)`
  `=P(1.005^n)-400\ 000(1.005^n)+400\ 000`
  `=(P-400\ 000)xx1.005^n+400\ 000\ \ text(… as required)`

 

ii. (2)  `text(Find)\ n\ text(such that)\ A_n<=0`

♦ Mean mark 38%

`text(S)text(ince)\  P=232\ 175.55`,

`(232\ 175.55-400\ 000)(1.005^n)+400\ 000<=0`

`167\ 824.45(1.005^n)` `>=400\ 000`
`1.005^n` `>=(400\ 000)/(167\ 824.45)`
`n ln1.005` `>=ln2.383443`
`n` `>=ln2.383443/ln1.005`
`n` `>=174.14\ \ text{(to 2 d.p.)}`

 

`:.\ text(There will be money left in the account for 175 months.)`

Financial Maths, 2ADV M1 2011 HSC 8c

When Jules started working she began paying $100 at the beginning of each month into a superannuation fund.

The contributions are compounded monthly at an interest rate of 6% per annum.

She intends to retire after having worked for 35 years.

  1. Let  `$P`  be the final value of Jules's superannuation when she retires after 35 years (420 months). Show that  `$P=$143\ 183`  to the nearest dollar.     (2 marks)

  2. Fifteen years after she started working Jules read a magazine article about retirement, and realised that she would need `$800\ 000` in her fund when she retires. At the time of reading the magazine article she had `$29\ 227` in her fund. For the remaining 20 years she intends to work, she decides to pay  `$M`  into her fund at the beginning of each month. The contributions continue to attract the same interest rate of 6% per annum, compounded monthly.

  3.  

    At the end of  `n`  months after starting the new contributions, the amount in the fund is  `$A_n`.

  4.  

      (1)  Show that  `A_2=29\ 227xx1.005^2+M(1.005+1.005^2)`.     (1 mark)

  5.  

      (2)  Find the value of  `M`  so that Jules will have $800 000 in her fund after the remaining 20 years (240 months).     (3 marks)

Show Answers Only
  1.  `text{Proof (See Worked Solutions)}`
  2. (1) `text{Proof (See Worked Solutions)}`
    (2) `$1514.48\ text{(nearest cent)}`
Show Worked Solutions
i.    `P_1` `=Pxxr=Pxx(1+(6%)/12)=100(1.005)`
  `P_2` `=P_1(1.005)+100(1.005^1)`
    `=100(1.005^2)+100(1.005^1)`
    `=100(1.005^2+1.005)`
  `P_3` `=(1.005)[100(1.005^2+1.005)]+100(1.005)`
    `=100(1.005+1005^2+1.005^3)`
    `\ \ \ \ vdots`
  `P_420` `=100(1.005+1.005^2+1.005^3 …+1.005^420)`

`=>\ text(GP where)\ \ a=1.005,\ \ r=1.005`

MARKER’S COMMENT: Common errors in this part included having the first term of the GP as 1 instead of 1.005 (note that the $100 goes in at the start of the month and earns interest before it is included in `$P_n)`.
`P_420` `=100((a(r^n-1))/(r-1))`
  `=100((1.005(1.005^420-1))/(1.005-1))`
  `=20\ 000(1.005(1.005^420-1))`
  `=$143\ 183.39`

 

`:.\ text{The final value of Jules’s superannuation is}`

`$143\ 183\ \ text{(to the nearest dollar)   … as required}`

 

♦ Mean mark 34% for part (ii)(1)

ii. (1)  `text(After 1 month,)\  A_1=29\ 227(1.005)+M(1.005)`

`A_2` `=A_1 (1.005)+M(1.005)`
  `=[29\ 227(1.005)+M(1.005)](1.005)+M(1.005)`
  `=29\ 227(1.005^2)+M(1.005^2)+M(1.005)`
  `=29\ 227(1.005^2)+M(1.005+1.005^2)\ \ text(… as required)`

 

ii. (2)  `text(Find)\ $M\ text(such that)\  A_n=$800\ 000\ text(after 240 months.)`

♦ Mean mark 49%

`A_240=29\ 227(1.005^240)+M(1.005+1.005^2+..+1.005^240)`

`=>\ GP\ text(where)\ a=1.005,\ text(and)\ r=1.005`

`800\ 000=29\ 227(1.005^240)+M((1.005(1.005^240-1))/(1.005-1))`

`M((1.005(1.005^240-1))/(1.005-1))=800\ 000-29\ 227(1.005^240)`

`M` `=(703\ 252.65)/(464.3511)`
  `=1514.484`..
`:.M` `=$1514.48\ \ text{(to the nearest cent)}`

Financial Maths, 2ADV M1 2011 HSC 5a

The number of members of a new social networking site doubles every day. On Day 1 there were 27 members and on Day 2 there were 54 members.

  1. How many members were there on Day 12?     (1 mark)

  2. On which day was the number of members first greater than 10 million?     (2 marks)

  3. The site earns 0.5 cents per member per day. How much money did the site earn in the first 12 days? Give your answer to the nearest dollar.     (2 marks)

Show Answers Only
  1. `55\ 296`
  2. `text(20th)`
  3. `$553`
Show Worked Solutions
MARKER’S COMMENT: Better responses stated the general term, `T_n` before any substitution was made, as shown in the worked solutions.

i.   `T_1=a=27`

`T_2=27xx2^1=54`

`T_3=27xx2^2=108`

`=>\ text(GP where)\ \ a=27,\ \ r=2`

`\ \ \ vdots`

`T_n` `=ar^(n-1)`
`T_12` `=27 xx 2^11=55\ 296`

 

`:.\ text(On Day 12, there are 55 296 members.)`

 

ii.   `text(Find)\ n\ text(such that)\  T_n>10\ 000\ 000`

MARKER’S COMMENT: Many elementary errors were made by students in dealing with logarithms. BE VIGILANT.
`T_n` `=27(2^(n-1))`
`27xx2^(n-1)` `>10\ 000\ 000`
`2^(n-1)` `>(10\ 000\ 000)/27`
`ln 2^(n-1)` `>ln((10\ 000\ 000)/27)`
`(n-1)ln2` `>ln(370\ 370.370)`
`n-1` `>ln(370\ 370.370)/ln 2`
`n-1` `>18.499…`
`n` `>19.499…`

 

`:.\ text(On the 20th day, the number of members >10 000 000.)`

 

iii.  `text(If the site earns 0.5 cents per day per member,)`

`text(On Day 1, it earns)\  27 xx 0.5 = 13.5\ text(cents)`

`text(On Day 2, it earns)\  27 xx 2 xx 0.5 = 27\ text(cents)`

`T_1=a=13.5`

`T_2=27`

`T_3=54`

`=>\ text(GP where)\ \ a=13.5,\ \ r=2`
 

`S_12=text(the total amount of money earned in the first 12 Days)`

♦ Mean mark 44%.
NOTE: This question can also be easily solved by making `S_12` the total sum of members (each day) and then multiplying by 0.5 cents.
`S_12` `=(a(r^n-1))/(r-1)`
  `=(13.5(2^12-1))/(2-1)`
  `=55\ 282.5\ \ text(cents)`
  `=552.825\ \ text(dollars)`

 

`:.\ text{The site earned $553 in the first 12 Days (nearest $).}`

Financial Maths, 2ADV M1 2012 HSC 15c

Ari takes out a loan of $360 000. The loan is to be repaid in equal monthly repayments, `$M`, at the end of each month, over 25 years (300 months). Reducible interest is charged at 6% per annum, calculated monthly.

Let  `$A_n`  be the amount owing after the `n`th repayment.

  1. Write down an expression for the amount owing after two months, `$A_2`.   (1 mark)

  2. Show that the monthly repayment is approximately $2319.50.   (2 marks)

  3. After how many months will the amount owing, `$A_n`, become less than $180 000.   (3 marks)

Show Answers Only
  1.  `$A_2=(360\ 000)(1.005^2)-M(1+1.005)`
  2. `text{Proof (See Worked Solutions)}`
  3. `202\ text(months)`
Show Worked Solutions
i.    `A_1` `=360\ 000(1+text(6%)/12)-M`
  `=360\ 000(1.005)-M`
`A_2` `=[360\ 000(1.005)-M](1.005)-M`
  `=360\ 000(1.005^2)-M(1.005)-M`
  `=360\ 000(1.005^2)-M(1+1.005)`

 

ii.  `A_n=360\ 000(1.005^n)-M(1+1.005^1+ … +1.005^(n-1))`

`text(When)\  n=300,\ A_n=0`

`0=360\ 000(1.005^300)-M(1+1.005^1+….+1.005^299)`

`360\ 000(1.005^300)` `=M((a(r^n-1))/(r-1))`
`M((1(1.005^300-1))/(1.005-1))` `=360\ 000(1.005^300)`
`:.M` `=((1\ 607\ 389.13)/692.994)`
  `~~2319.50\ \ \ text(… as required)`

 

iii.   `text(Find)\ n\ text(such that)\  $A_n<$180\ 000`

`360\ 000(1.005^n)-2319.50((1.005^n-1)/(1.005-1))` `<180\ 000`
`360\ 000(1.005^n)-463\ 900(1.005^n-1)` `<180\ 000`
`-103\ 900(1.005^n)+463,900` `<180\ 000`
♦ Mean mark 38%
MARKER’S COMMENT: Challenging calculations using logarithms are common in this topic. A high percentage of students consistently struggle in this area.
`103\ 900(1.005^n)` `>283\ 900`
`1.005^n` `>(283\ 900)/(103\ 900)`
`n(ln1.005)` `>ln((283\ 900)/(103\ 900))`
`n` `>1.005193/0.0049875`
`n` `>201.54`

 

`:.\ text(After 202 months,)\  $A_n< $180\ 000.`

Probability, 2ADV S1 2013 HSC 15d

Pat and Chandra are playing a game. They take turns throwing two dice. The game is won by the first player to throw a double six. Pat starts the game.

  1. Find the probability that Pat wins the game on the first throw.     (1 mark)

  2. What is the probability that Pat wins the game on the first or on the second throw?     (2 marks)

  3. Find the probability that Pat eventually wins the game.     (2 marks)

Show Answers Only
  1. `1/36`
  2. `(2521)/(46\ 656)\ \ text(or)\ \ 0.054`
  3. `36/71`
Show Worked Solutions

i.   `P\ text{(Pat wins on 1st throw)}=P(W)`

`P(W)` `=P\ text{(Pat throws 2 sixes)}`
  `=1/6 xx 1/6`
  `=1/36`

 

ii.  `text(Let)\ P(L)=P text{(loss for either player on a throw)}=35/36`

`P text{(Pat wins on 1st or 2nd throw)}` 

♦♦ Mean mark 33%
MARKER’S COMMENT: Many students did not account for Chandra having to lose when Pat wins on the 2nd attempt.

`=P(W) + P(LL W)`

`=1/36\ + \ (35/36)xx(35/36)xx(1/36)`

`=(2521)/(46\ 656)`

`=0.054\ \ \ text{(to 3 d.p.)}`

 

iii.  `P\ text{(Pat wins eventually)}`

`=P(W) + P(LL\ W)+P(LL\ LL\ W)+ … `

`=1/36\ +\ (35/36)^2 (1/36)\ +\ (35/36)^2 (35/36)^2 (1/36)\ +…`

 
`=>\ text(GP where)\ \ a=1/36,\ \ r=(35/36)^2=(1225)/(1296)`

♦♦♦ Mean mark 8%!
 COMMENT: Be aware that diminishing probabilities and `S_oo` within the Series and Applications are a natural cross-topic combination.

 
`text(S)text(ince)\ |\ r\ |<\ 1:`

`S_oo` `=a/(1-r)`
  `=(1/36)/(1-(1225/1296))`
  `=1/36 xx 1296/71`
  `=36/71`

 

`:.\ text(Pat’s chances to win eventually are)\  36/71`.

Financial Maths, 2ADV M1 2013 HSC 13d

A family borrows $500 000 to buy a house. The loan is to be repaid in equal monthly instalments. The interest, which is charged at 6% per annum, is reducible and calculated monthly. The amount owing after  `n`  months, `$A_n`, is given by

`qquad qquadA_n=Pr^n-M(1+r+r^2+ \ .... +r^(n-1))\ \ \ \ \ \ \ \ \ ` (DO NOT prove this)

where  `$P`  is the amount borrowed, `r=1.005`  and  `$M`  is the monthly repayment.

  1. The loan is to be repaid over 30 years. Show that the monthly repayment is $2998 to the nearest dollar.     (2 marks)

  2. Show that the balance owing after 20 years is $270 000 to the nearest thousand dollars.             (1 mark)

After 20 years the family borrows an extra amount, so that the family then owes a total of $370 000. The monthly repayment remains $2998, and the interest rate remains the same.

  1. How long will it take to repay the $370 000?     (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `text{Proof (See Worked Solutions)}`
  3. `text(193 months)`
Show Worked Solutions

i.    `text(Find)\  $M\  text(such that the loan is repaid over 30 years.)`

`n=30xx12=360\ text(periods)\ \ \   r=1+6/12%=1.005`

`A_360` `=500\ 000 (1.005^360)-M(1+1.005+..+1.005^359)=0`

`=>GP\ text(where)\ a=1,\ \ r=1.005,\ \ \ n=360`

`M((1(1.005^360-1))/(1.005-1))` `=500\ 000(1.005^360)`
`M(1004.515)` `=3\ 011\ 287.61`
`M` `=2997.75`

 

`:.$M=$2998\ \ text{(nearest dollar) … as required}`

 

 ii.    `text(Find)\  $A_n\ text(after 20 years)\ \ \ =>n=20xx12=240` 

`A_240` `=500\ 000(1.005^240)-2998(1+1.005+..+1.005^239)`
  `=1\ 655\ 102.24-2998((1(1.005^240-1))/(1.005-1))`
  `=269\ 903.63`
  `=270\ 000\ \ text{(nearest thousand) … as required}`
MARKER’S COMMENT: Within the GP formula, many students incorrectly wrote the last term as `1.005^240` rather than `1.005^239`. Note `T_n=ar^(n-1)`.

 

 

iii.  `text(Loan)=$370\ 000`

`text(Find)\  n\  text(such that)\  $A_n=0,\ \ \ M=$2998`

`A_n=370\ 000(1.005^n)-2998(1+1.005+..+1.005^(n-1))=0`

♦♦ Mean mark 33%
COMMENT: Another good examination of working with logarithms. Students should understand why they must ’round up’ their answer in this question.
`370\ 000(1.005^n)` `=2998((1(1.005^n-1))/(1.005-1))` 
`370\ 000(1.005^n)` `=599\ 600(1.005^n-1)`
`229\ 600(1.005^n)` `=599\ 600`
`ln1.005^n` `=ln((599\ 600)/(229\ 600))`
`n` `=ln2.6115/ln1.005`
`n` `=192.4`

 
`:.\ text(The loan will be repaid after 193 months.)`

Financial Maths, 2ADV M1 2013 HSC 12c

Kim and Alex start jobs at the beginning of the same year. Kim's annual salary in the first year is $30,000 and increases by 5% at the beginning of each subsequent year. Alex's annual salary in the first year is $33,000, and increases by $1,500 at the beginning of each subsequent year.

  1. Show that in the 10th year, Kim's annual salary is higher than Alex's annual salary.     (2 marks)

  2. In the first 10 years how much, in total, does Kim earn?     (2 marks)

  3. Every year, Alex saves `1/3` of her annual salary. How many years does it take her to save $87,500?     (3 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `$377\ 336.78`
  3. `text(7  years)`
Show Worked Solutions

i.    `text(Let)\ \ K_n=text(Kim’s salary in Year)\  n`

`{:{:(K_1=a=30\ 000),(K_2=ar^1=30\ 000(1.05^1)):}}{:(\ =>\ GP),(\ \ \ \ \ \ a=30\ 000),(\ \ \ \ \ \ r=1.05):}`

`vdots`

`:.K_10=ar^9=30\ 000(1.05)^9=$46\ 539.85`

 

`text(Let)\ \ A_n=text(Alex’s salary in Year)\ n`

`{:{:(A_1=a=33\ 000),(A_2=33\ 000+1500=34\ 500):}}{:(\ =>\ AP),(\ \ \ \ \ \ a=33\ 000),(\ \ \ \ \ \ d=1500):}`

`vdots`

`A_10=a+9d=33\ 000+1500(9)=$46\ 500`

`=>K_10>A_10`
 

`:.\ text(Kim earns more than Alex in the 10th year)`

 

ii.    `text(In the first 10 years, Kim earns)`

`K_1+K_2+\  ….+ K_10`

`S_10` `=a((r^n-1)/(r-1))`
  `=30\ 000((1.05^10-1)/(1.05-1))`
  `=377\ 336.78`

 

`:.\ text(In the first 10 years, Kim earns $377 336.78)`

 

iii.   `text(Let)\ T_n=text(Alex’s savings in Year)\ n`

`{:{:(T_1=a=1/3(33\ 000)=11\ 000),(T_2=a+d=1/3(34\ 500)=11\ 500),(T_3=a+2d=1/3(36\ 000)=12\ 000):}}{:(\ =>\ AP),(\ \ \ \ a=11\ 000),(\ \ \ \ d=500):}`
 

`text(Find)\ n\ text(such that)\ S_n=87\ 500`

♦ Mean mark 45%.
IMPORTANT: Using the AP sum formula to create and then solve a quadratic in `n` is challenging and often examined. Students need to solve and interpret the solutions.
`S_n` `=n/2[2a+(n-1)d]`
`87\ 500` `=n/2[22\ 000+(n-1)500]`
`87\ 500` `=n/2[21\ 500+500n]`
`250n^2+10\ 750n-87\ 500` `=0`
`n^2+43n-350` `=0`
`(n-7)(n+50)` `=0`

 
`:.n=7,\ \ \ \ n>0`

`:.\ text(Alex’s savings will be $87,500 after 7 years).`