SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Number, NAPX-p107114v02 SA

A charity calculates its total donations every month.

Over a six month period, the amounts they calculate are as follows:

$1520, $1270, $1600, $1310, $1430, $1288

What is the mean monthly donation the charity received over this 6 month period?

Show Answers Only

`$1403`

Show Worked Solution
`text(Mean)` `= (1520 + 1270 + 1600 + 1310 + 1430)/6`
  `= 8418/6`
  `= $1403`

Statistics, NAPX-p107114v01 SA

Over a week, a pensioner drove the following distances, in kilometres, in her car.

12, 18, 11, 9, 13, 16, 12

What is his mean distance travelled in the car each day over the week?

 

Show Answers Only

`text(13 km)`

Show Worked Solution
`text(Mean)` `= (12 + 18 + 11 + 9 + 13 + 16 + 12)/7`
  `= 91/7`
  `= 13\ text(kilometres)`

Probability, NAPX-p170160v02 SA

A spinning wheel is divided into 56 equal sectors that are coloured either red or blue.

Chablis spins the wheel and has a 1 in 8 chance of landing in a sector coloured red.

How many blue sectors are there on the spinning wheel?

 

Show Answers Only

`49`

Show Worked Solution
`text(Number of red sectors)` `= 1/8 xx 56`
  `= 7`

 

`text(Number of blue sectors)` `=\ text(Total sectors – Red sectors)`
  `= 56 – 7`
  `= 49`

Probability, NAPX-p170160v01 SA

Harley has bag that contains 32 balls that are coloured either black or white.

Harley chose a ball without looking and had the chance of 3 in 8 of choosing a white ball.

How many black balls are in Harley's bag?

 

Show Answers Only

`20`

Show Worked Solution
`text(Number of white balls)` `= 3/8 xx 32`
  `= 12`

 

`text(Number of black balls)` `=\ text(Total balls – white balls)`
  `= 32 – 12`
  `= 20`

Algebra, NAPX-p106742v02

A Cartesian plane is shown below.
 


 

Which statement is true?

 
   `R` is located where  `x < 0`  and  `y > 0`
 
   `N` is located where  `x < 0`  and  `y < 0`
 
   `M` is located where  `x > 0`  and  `y < 0`
 
   `Q` is located where  `x < 0`  and  `y < 0`

Show Answers Only

`N\ text(is located where)\ \ x < 0\ \ text(and)\ \ y < 0`

Show Worked Solution

`text(Points left of the)\ y text(-axis): \ x<0`

`text(Points below the)\ x text(-axis): \ y<0`

`:. N\ text(is located where)\ \ x < 0\ \ text(and)\ \ y < 0\ \ text(is correct.)`

Algebra, NAPX-p106742v01

A Cartesian plane is shown below..
 


 

Which statement is true?

 
   `S` is located where  `x < 0`  and  `y < 0`
 
   `T` is located where  `x < 0`  and  `y > 0`
 
   `Z` is located where  `x > 0`  and  `y < 0`
 
   `Y` is located where  `x = 0`  and  `y > 0`

Show Answers Only

`Z\ text(is located where)\ \ x > 0\ \ text(and)\ \ y < 0`

Show Worked Solution

`text(Points right of the)\ y text(-axis): \ x>0`

`text(Points below the)\ x text(-axis): \ y<0`

` :. Z\ text(is located where)\ \ x > 0\ \ text(and)\ \ y < 0\ \ text(is correct.)`

Number, NAPX-p109430v02 SA

Alejandro makes sangria for his Spanish restaurant.

A glass of sangria has a mass of 240 grams and contains 120 millilitres of sangria.

What is the total mass of glasses that contain 3.6 litres of sangria?

  kilograms

Show Answers Only

`text(7.2 kilograms)`

Show Worked Solution

`text(1 litre = 1000 mL)`

`text(3.6 litres = 3600 mL)`

`text(Number of glasses)` `= (3600)/120`
  `= 30`

 
`text(S)text(ince every glass weighs 240 grams and)`

`text(1 kilogram = 1000 grams)`

`text(Total mass)` `= 30 xx 240`
  `= 7200\ text(grams)`
  `= 7.2\ text(kg)`

Number, NAPX-p109430v01 SA

Fillon produces fresh milk.

A bottle of milk contains 500 millilitres and has a mass of 600 grams.

How many litres of milk has Fillon produced if the bottles have a total mass of 15 kilograms?

  litres

Show Answers Only

`text(12.5 Litres)`

Show Worked Solution

`text(1 kilogram = 1000 grams)`

`text(15 kilograms = 15 000 grams)`

`text(Number of bottles)` `= (15\ 000)/600`
  `= 25`

 
`text(S)text(ince there is 500 mL in each bottle and)`

`text(1 Litre = 1000 mL,)`

`text(Volume)` `= 25 xx 500`
  `= 12\ 500\ text(mL)`
  `= 12.5\ text(Litres)`

Geometry, NAPX-p109193v02 SA

A scale diagram is shown below and represents the distances between 3 cities.
 


 

The distance from City A to City B is 84 kilometres.

What is the distance from City B to City C?

  kilometres

Show Answers Only

`text(36 km)`

Show Worked Solution
`text(Distance of one grid width)` `= 84/7`
  `= 12\ text(km)`

 
`text(City B and City C are 3 grids apart)`

`text(Distance City B to City C)` `= 12 xx 3`
  `= 36\ text(km)`

Geometry, NAPX-p109193v01 SA

The ports A, B, and C are marked in the scale diagram below.
 


 

The distance from Port A to Port B is 35 kilometres.

What is the distance from Port B to Port C?

  kilometres

Show Answers Only

`text(52.5 km)`

Show Worked Solution
`text(Distance of one grid)` `= 35/4`
  `= 8.75\ text(km)`

 
`text(Port B and Port C are 6 grid widths apart)`

`text(Distance Port B to Port C)` `= 8.75 xx 6`
  `= 52.5\ text(km)`

Measurement, NAPX-p111988v02

Mario sketches an irregular plot of land, pictured below.
 


 

What is the perimeter of this polygon in metres?

 
   167 m
 
   192 m
 
   244 m
 
   248 m
 
   261 m
Show Answers Only

`248\ text{m}`

Show Worked Solution

`text{Adding sides clockwise from bottom left:}`

`text{Perimeter of the shape}` `= 50 + 15 + 30 + 17 + 14 + 13 + 34 + 45`
  `= 248 \ text{metres}`

Number, NAPX-p110751v02 SA

In a bulk food supermarket, a kilogram of pepper costs $14.

Nancy bought 2.65 kilograms of pepper for her restaurant.

How much did Nancy pay for the pepper?

$  

Show Answers Only

`$37.10`

Show Worked Solution

`text(C)text(ost of 1 kg = $14)`

`text(C)text(ost of 2 kg) = 2 xx 14 = $28`

`text(C)text(ost of 0.1 kg) = 0.1 xx $14 = $1.40`

`text(C)text(ost of 0.65 kg)` `= 6 xx 1.4 + 0.70`
  `= $9.10` 

 

`:.\ text(C)text(ost of 2.65 kg)` `= 28 + 9.1`
  `= $37.10` 

Number, NAPX-p110751v01 SA

A kilogram of apples cost $8.

Danica bought 6.35 kilograms of apples.

How much did Danica pay for the apples?

$  

Show Answers Only

`$50.80`

Show Worked Solution

`text(C)text(ost of 1 kg = $8)`

`text(C)text(ost of 6 kg) = 6 xx 8 = $48`

`text(C)text(ost of 0.1 kg) = 0.1 xx 8 = $0.80`

`text(C)text(ost of 0.35 kg)` `= 3 xx 0.8 + 0.4`
  `= $2.80` 

 

`:.\ text(C)text(ost of 6.35 kg)` `= 48 + 2.80`
  `= $50.80` 

Measurement, NAPX-p169879v02 SA

Timothy sketched a plot of land with the following measurements in metres.
 


 

What is the area of the land in square metres?

  square metres

Show Answers Only

`text(487 m)²`

Show Worked Solution

`text(Divide the shape into 3 parts:)`
 

`text(Total Area)` `=\ text(Area 1 + Area 2 + Area 3)`
  `= (15 xx 12) + (23 xx 10) + (1/2 xx 11 xx 14)`
  `= 180 + 230 + 77`
  `= 487\ text(m)²`

Measurement, NAPX-p169879v01 SA

Hana sketches a shape with the following measurements in centimetres.
 

 
 

What is the area of the shape sketched by Hana?

  square centimetres

Show Answers Only

`text(90 cm)²`

Show Worked Solution

`text(Divide the shape into two parts.)`
 

`text(Total Area)` `=\ text(Area of triangle + Area of rectangle)`
  `= (1/2 xx 4 xx 9) + (8 xx 9)`
  `= 18 + 72`
  `= 90\ text(cm)²`

Number, NAPX-p111991v02 SA

Justin went to a lolly shop to buy some sweets and spent $12.

He bought a chocolate bar that cost $5 and 7 pieces of liquorice that cost 40 cents each.

The rest of his money was spent on musk sticks that costs $0.30 each.

How many musk sticks did he buy?

Show Answers Only

`18`

Show Worked Solution
`text(Money left)` `= 12 – 5 – (7 xx 0.40)`
  `= 7-2.80`
  `=$4.20`

 

`:.\ text(Musk sticks)` `= 4.2 -: 0.3`
  `=4.2 -: 3/10`
  `=4.2 xx 10/3`
  `= 18`

Number, NAPX-p111991v01 SA

Joanna went to the supermarket and spent $52.

She bought $15 worth of meat, 10 energy drinks costing $1.90 each and some bottles of water that cost $1.20 each.

How many bottles of water did she buy?

Show Answers Only

`15`

Show Worked Solution
`text(Money left for water)` `= 52 – 15 – (10 xx 1.9)`
  `= 52-15-19`
  `=$18`

 

`:.\ text(Bottles of water)` `= 18 ÷ 1.2`
  `=18 -: 6/5`
  `=18 xx 5/6`
  `= 15`

Measurement, NAPX-p169867v02

Emily walks for 17 minutes to get from her house to Diamond Station.

She then travels by train to Ruby Station.

Emily then walks 21 minutes to the supermarket where she works.
  

   

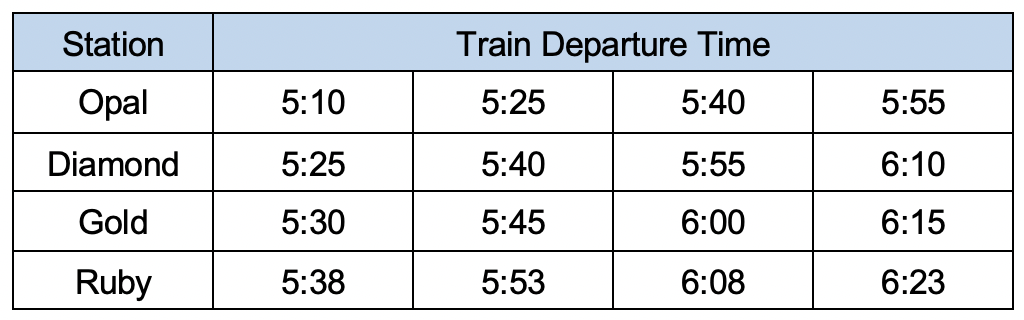
If Emily's shift starts at 6:30, what is the latest time she can leave home to arrive on time?

 
 4:53
 
 5:08
 
 5:23
 
 5:38

Show Answers Only

`5:38`

Show Worked Solution

`text(Working backwards from arriving at the supermarket at 6:30)`

`text(6:30 less 21 minutes walking = 6:09)`

`text(1st train to arrive before 6:09 leaves Diamond Station at 5:55)`

`text(5:55 less than 17 minutes walking = 5:38)`

`:.\ text(Emily must leave her house by 5:38.)`

Measurement, NAPX-p169867v01

It takes Terry 32 minutes to walk from his home to Train Station A.

He then travels by train to Station C.

Terry then walks to an amusement park which takes him 18 minutes.
 

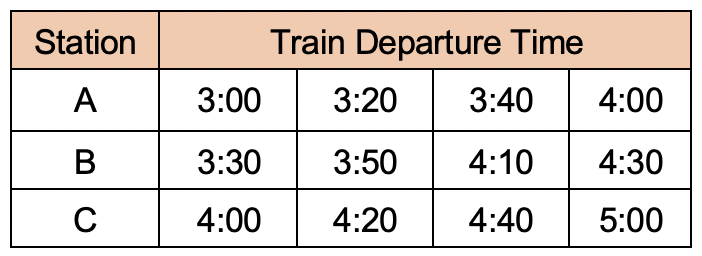
What is the latest time that Terry can leave his home to arrive at the amusement park by 5:00?

 
 2:28
 
 2:48
 
 3:08
 
 3:28

Show Answers Only

`3:08`

Show Worked Solution

`text(Working backwards from arriving at the amusement park at 5:00)`

`text(5:00 less 18 minutes walking = 4:42)`

`text(1st train to arrive before 4:42 leaves Station A at 3:40)`

`text(3:40 less than 32 minutes walking = 3:08)`

`:.\ text(Terry must leave his house by 3:08.)`

Measurement, NAP-L4-CA30

A truck driver plans to drive from Cairns to the Gold Coast.

The driving time for the journey is 19 hours.

The driver must stop for at least 8 hours rest after every 10 hours of driving.

What is the latest time that the driver can depart Cairns on Monday to arrive in the Gold Coast at 2 pm on Tuesday?

1 am 11 am 1 pm 7 pm
 
 
 
 
Show Answers Only

`text(11 am)`

Show Worked Solution
`text(Total travel time)` `= 19 + 8`
  `= 27\ text(hours)`

 

`:.\ text(Driver must leave Cairns)`

`= 2\ text(pm Tuesday less 27 hours)`

`= 11\ text(am Monday)`

Algebra, NAP-L4-CA29

A florist uses the formula below to estimate the delivery time for an order.

`t = 11 + 3d`

where  `t`  is the time in minutes and  `d`  is the delivery distance in kilometres.

Select all the statements which are true.

 
 A 5-kilometre delivery should take 46 minutes.
 
 A 4-kilometre delivery will take 3 minutes longer than a 3-kilometre delivery.
 
 Every extra kilometre triples the total delivery time.
 
 All deliveries take at least 11 minutes.
Show Answers Only

`text(2nd and 4th statements)`

Show Worked Solution

`text(Correct statements:)`

`text(A 4-kilometre delivery will take 3 minutes longer than a 3-kilometre delivery.)`

`text(All deliveries take at least 11 minutes.)`

Number, NAP-L4-CA24

An ancient coin is made up of gold and silver in the ratio 1:3.

The coin weighs 21.65 grams.

How many grams of silver are in the ancient coin?

`5.4125` `7.217` `14.433` `16.2375`
 
 
 
 
Show Answers Only

`16.2375`

Show Worked Solution

`text(Ratio)\ 1:3 -> 4\ text(parts)`

`text(1 part)` `= 21.65/4`
  `= 5.4125`

 

`text(Silver weight)` `= 3 xx 5.4125`
  `= 16.2375`

Measurement, NAP-L4-CA23

A rectangular garden bed is 7 metres long by 4 metres wide.

The garden bed is filled with soil to a height of 50 centimetres.
 


 

How many cubic metres of soil are needed to fill the garden bed?

11 14 22 1400
 
 
 
 
Show Answers Only

`14\ text(m³)`

Show Worked Solution

`50\ text(cm) \ => \ 0.5\ text(metre)`

`text(Soil needed)` `= 7 xx 4 xx 0.5`
  `= 14\ text(m³)`

Algebra, NAP-L3-NC08 SA

Sabre is saving to buy a new skateboard.

After one week she has saved $11.

She then saves the same amount of money each week.
 

\begin{array} {|l|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \text{Week}\ \rule[-1ex]{0pt}{0pt} &  1  &\ \ 2\ \ &\ \ 3 \ &\ \ 4\ \ &\ \ 5\ \ \\
\hline
\rule{0pt}{2.5ex} \ \text{Total amount saved}\ \rule[-1ex]{0pt}{0pt} & $11  & $18  & $25 & $32 & $39\\
\hline
\end{array} 

How much money will Sabre have saved by the end of week 10?

$  
 
Show Answers Only

\($74\)

Show Worked Solution

\(\text{Total saved each week (after week 1)}\)

\(= $7\)

\(\text{Total saved at end of week }5 = $39\)
 

\(\therefore\ \text{Total savings at end of week 10}\)

\(=39+(5\times 7)\)

\(=39+35\)

\(=$74\)

Measurement, NAP-L3-CA40

Ken puts two cardboard squares together, as shown in the diagram below.

The squares have areas of 4 cm² and 25cm².

Ken draws a line from the bottom left to top right, and shades the region above the line.
 


 

What is the area of the shaded region?

13.5 cm² 14.5 cm² 17.5 cm² 19 cm²
 
 
 
 
Show Answers Only

`text(17.5 cm²)`

Show Worked Solution

`text(Small square → 2 cm sides)`

`text(Large square → 5 cm sides)`
 

 
 

`:.\ text(Shaded Area)` `= 1/2 xx b xx h`
  `= 1/2 xx 5 xx 7`
  `= 17.5\ text(cm²)`

Number, NAP-L3-CA37

Pat, Mitch and Josh entered a long distance relay as a team.

They divided the total distance into 20 equal sections.

Pat ran  `9/20`  of the total distance.

Mitch ran  `3/20`  more of the total distance than Josh.

What fraction of the total distance did Josh ran?

`4/20` `7/20` `8/20` `17/20`
 
 
 
 
Show Answers Only

`4/20`

Show Worked Solution

`text(Total distance Mitch and Josh run) = 11/20`

`=>\ text(Mitch runs) = 7/20`

`=>\ text(Josh runs) = 4/20`

Statistics, NAP-L3-CA35

Students at a high school were surveyed to find whether they did exercise before school.

The graph below shows the results.
 


 

There were 150 17-year-old students at the high school.

How many 17-year-old students responded 'Every Day'?

`14` `30` `38` `45` `60`
 
 
 
 
 
Show Answers Only

`45`

Show Worked Solution

`text(30% of 17-year-old responded ‘Every Day’.)`

`:.\ text(Number)` `= 0.3 xx 150`
  `= 45`

Number, NAP-L4-CA33 SA

Genghis and Kublai are shooting arrows at a target.

Genghis shoots an arrow every 3 seconds.

Kublai shoots an arrow every 8 seconds.

They shoot their first arrow together at 10:00 am.

How many more times will they shoot arrows at exactly the same time in the next 3 minutes?

 
Show Answers Only

`7`

Show Worked Solution

`text(Every 24 seconds, arrows shot at the same time.)`

`=>\ text(Arrows are shot at the same time:)`

`24, 48, 72, 96, 120, 144, 168\ text(seconds)`

`:. 7\ text{more times  (time ≤ 180 seconds)}`

Number, NAP-L3-CA34 SA

Genghis and Kublai are shooting arrows at a target.

Genghis shoots an arrow every 3 seconds.

Kublai shoots an arrow every 8 seconds.

They shoot their first arrow together at 10:00 am.

How many more times will they shoot arrows at exactly the same time in the next 3 minutes?

 
Show Answers Only

`7`

Show Worked Solution

`text(Every 24 seconds, arrows shot at the same time.)`

`=>\ text(Arrows are shot at the same time:)`

`24, 48, 72, 96, 120, 144, 168\ text(seconds)`

`:. 7\ text{more times  (time ≤ 180 seconds)}`

Probability, NAP-L3-CA33 SA

Rachel has a bag that contains 6 blue and 4 green balls.

She selects one ball at random and records its colour. The ball is then put back into the bag.

Rachel does this 50 times.

How many times should Rachel expect to select a green ball from the bag?

 
Show Answers Only

`20`

Show Worked Solution

`P(text(picking green)) = 4/10 = 2/5`

`:.\ text(Expected green balls)` `= 2/5 xx 50`
  `= 20`

Measurement, NAP-L3-CA32 SA

Ronald places 5 identical hexagonal tiles side-by-side to make the pattern pictured below.
 


 

Each tile has a perimeter of 24 cm and is in the shape of a regular hexagon.

What is the perimeter of the large shape, in centimetres?

   cm
Show Answers Only

`64\ text(cm)`

Show Worked Solution
`text(Length of 1 side)` `= 24 ÷ 6`
  `= 4\ text(cm)`

 

`:.\ text(Perimeter)` `= 16 xx 4`
  `= 64\ text(cm)`

Measurement, NAP-G2-37v1

Dom times how long it takes her to get home on the bus each day.

Last year, Dom's quickest bus ride home from school was 14 minutes and 23 seconds.

She recorded the time like this.

This year, Dom's quickest bus ride home was 3 minutes and 35 seconds faster.

What is the quickest time this year?

Show Answers Only

`10:48`

Show Worked Solution

`text(One strategy:)`

`text(14:23 less 3:35)` `=\ text(11:23 less 0:35)`
  `=\ text(11:00 less 0:12)`
  `=\ text(10:48)`

Number and Algebra, NAP-J2-42 SA

Bert and Ernie are standing in a line, waiting to go into their classroom.

There are:

  • 9 people between Bert and Ernie.
  • 14 people in front of Bert including Ernie.
  • 20 people behind Ernie including Bert.

In total, how many people are in the line?
Show Answers Only

`25`

Show Worked Solution

`text(The line-up will be:)`

`text(10 people → Bert → 9 people → Ernie → 4 people)`

`:.\ text(Total people in line)`

`= 10 + 1 + 9 + 1 + 4`

`= 25`

Number and Algebra, NAP-K2-42 SA

During the week, a cake shop sells cupcakes for $56.00 a dozen.

On Saturday afternoon, the cost of the cupcakes is discounted by 25%.

How much will a dozen cupcakes cost on Saturday afternoon?

$  
Show Answers Only

`$42`

Show Worked Solution

`text(Price reduced by 25%) = 1/4`
 

`text(After the discount,)`

`text(Price)` `= 3/4 xx 56`
  `= 3 xx 14`
  `= $42`

Number and Algebra, NAP-K2-41

Clarice has read 40 pages of a 60-page book.

Select all numbers that show the fraction of the book Clarice has left to read.

     `4/10`             `1/4`               `1/3`       
 
 
 
     `2/3`             `6/4`               `2/6`       
 
 
 
Show Answers Only

`1/3, 2/6`

Show Worked Solution
`text(Fraction left)` `= text(pages left)/text(total pages)`
  `= 20/60`

 
`:. 1/3, 2/6`

Measurement, NAP-K2-40

Duke looked at the calendar on 20 March.

He plans to go to a rodeo on 13 April and circled this on the calendar below.
 


 

What day of the week is 20 March?

Tuesday Wednesday Thursday Saturday Sunday
 
 
 
 
 
Show Answers Only

`text(Thursday)`

Show Worked Solution

`text(Working backwards:)`

`text(13 April → Sunday)`

`text(6 April → Sunday)`

`text(30 March → Sunday)`

`text(23 March → Sunday)`
 

`:. 20\ text(March is a Thursday)`

Number and Algebra, NAP-K2-39

Ruby thinks of a number that follows the rules below.

  • the number is odd
  • the number lies between 4300 and 5100
  • the number's digits add up to 12

Select all of the possible numbers that Ruby could be thinking of.

`4411` `5115` `5025` `4503` `4170` `4602`
 
 
 
 
 
 
Show Answers Only

`text(5025 and 4503)`

Show Worked Solution

`text(5025 and 4503 satisfy all the rules.)`

Number and Algebra, NAP-K2-38

Mike has 84 brochures to give out at a conference.

He puts an equal number of brochures onto each table at the conference and has none left over.

Select all of the options that could show the number of tables at the conference.

`6` `7` `13` `16` `24`
 
 
 
 
 
Show Answers Only

`6 and 7`

Show Worked Solution

`text(Only when 84 is divided by either  6 or 7)`

`text(will the answer be a whole number.)`

Number, NAP-K4-NC04

In a racing car season, the top three finishers in each race are awarded points.
 

Vangio was awarded a total of 25 points.

What is the greatest number of races in which Vangio could have been in the top three?

5 6 7 8
 
 
 
 
Show Answers Only

`6`

Show Worked Solution

`text(The greatest number of top 3 finishes occur with)`

`text(the following points results:)`

`8 + 5 + 3 + 3 + 3 + 3 = 25`

`:. 6\ text(events is the highest.)`

Number, NAP-K3-NC07

Ruby thinks of a number that follows the rules below.

  • the number is odd
  • the number is lies between 4300 and 5100
  • the number's digits add up to 12

Select all of the possible numbers that Ruby could be thinking of.

`4411` `5115` `5025` `4503` `4170` `4602`
 
 
 
 
 
 
Show Answers Only

`text(5025 and 4503)`

Show Worked Solution

`text(5025 and 4503 are the only options that satisfy all the rules.)`

Statistics, NAP-K3-CA36

Two fishing boats record the number of tuna they catch on four fishing trips.
 

 
How many more tuna did Boat 2 catch than Boat 1 in total over the four trips.

 
Show Answers Only

`60`

Show Worked Solution
`text(Boat 1 tuna)` `= 140 + 120 + 40 + 55`
  `= 355`
`text(Boat 2 tuna)` `= 105 + 130 + 95 + 85`
  `= 415`

 
`:.\ text(Extra tuna caught by Boat 2)`

`= 415 – 355`

`= 60`

Measurement, NAP-K3-CA34

Aragorn is fencing a paddock on his property. The total length of fencing he requires is 8.2 kilometres.

The length of the paddock is 2.8 kilometres.
 

 
How wide is the paddock?

Write your answer, in kilometres to one decimal place?

    kilometres
Show Answers Only

`1.3`

Show Worked Solution

`text(Express as a perimeter equation:)`

`2 xx 2.8 + 2x` `= 8.2`
`2x` `= 2.6`
`:. x` `= 1.3\ text(km)`

Number, NAP-K3-CA31

A biscuit factory produces 72 000 packets of biscuits in a year.

Production is expected to increase by 1500 packets each year.

Which of these will give the best estimate of the production of the biscuit factory in 3 years' time?

 
 `72\ 000 + 1500 xx 3`
 
 `(72\ 000 + 1500) xx 3`
 
 `72\ 000 + 1500 + 3`
 
 `(72\ 000 + 3) xx 1500`
Show Answers Only

`72\ 000 + 1500 xx 3`

Show Worked Solution
`text(Estimate)`  `= 72\ 000+ 1500 + 1500 + 1500` 
  `= 72\ 000 + 1500 xx 3`

Measurement, NAP-K3-CA30

Sabre want to frame a square photograph that has an area of 64 square centimetres.

Sabre makes the frame using 4 strips of aluminium.

Each strip is 4 centimetres longer than the width of the photograph.

What is the total length of the 4 strips aluminium he uses to make the frame?

`text(32 cm)` `text(40 cm)` `text(48 cm)` `text(56 cm)`
 
 
 
 
Show Answers Only

`text(48 cm)`

Show Worked Solution

`text(Side length of photograph)`

`= sqrt64`

`= 8\ text(cm)`
 

`:.\ text(Total length of aluminium)`

`= 4 xx (8 + 4)`

`= 4 xx 12`

`= 48\ text(cm)`

Number, NAP-K4-CA27

A brand of pasta is sold in two different packets.
 

 
What is the difference in the price per kilogram of these two packets?

$1.50 $3.00 $3.60 $7.20
 
 
 
 
Show Answers Only

`$3.00`

Show Worked Solution

`text(Convert to price per kg)`

`text(Packet 1)`

`200\ text(g) = $1.80`

`1\ text(kg) = 5 xx 1.80 = $9`

 

`text(Packet 2)`

`750\ text(g) = $9`

`100\ text(g) = 9.00 ÷ 7.5 = $1.20`

`1\ text(kg) = 1.20 xx 10 = $12`

 

`:.\ text(Difference per kg)`

`= 12 – 9`

`= $3.00`

Algebra, NAP-K4-CA25

55 students at a school need to choose a language to study between Japanese, Mandarin and French.

  • Ten more students chose Japanese than Mandarin.
  • Half as many students chose French than Mandarin.

How many students chose to study Japanese?

9 11 13 28
 
 
 
 
Show Answers Only

`28`

Show Worked Solution

`text(Strategy 1)`

`text(By trial and error):`

`text(Consider option 4)`

`text(If  J) = 28,\ text(M) = 18,\ text(F) = 9`

`=>\ text(total students = 55)`

`:. 28\ text(chose Japanese)`

 

`text{Strategy 2 (Algebra)}:`

`text(Expressing the information as equations:)`

`text(J) = text(M) + 10 …\ text{(1)}`

`text(F) = 1/2\ text(M) …\ text{(2)}`

`text(J + M + F) = 55 …\ text{(3)}`
 

`text{Substitute (1) and (2) into (3)}`

`text(M) + 10 + text(M) + 1/2 text(M)`  `= 55` 
`5/2 text(M)`  `= 45` 
`text(M)`  `= 18` 
`:.\ text(J)`  `= 28` 

Algebra, NAP-K4-CA23

A biscuit factory produces 72 000 packets of biscuits in a year.

Production is expected to increase by 1500 packets each year.

Which of these will give the best estimate of the production of the biscuit factory in 3 years' time?

 
 `72\ 000 + 1500 xx 3`
 
 `(72\ 000 + 1500) xx 3`
 
 `72\ 000 + 1500 + 3`
 
 `(72\ 000 + 3) xx 1500`
Show Answers Only

`72\ 000 + 1500 xx 3`

Show Worked Solution
`text(Estimate)`  `= 72\ 000+ 1500 + 1500 + 1500` 
  `= 72\ 000 + 1500 xx 3`

Algebra, NAP-K4-CA22

What is the equation for the line shown?
 


 

`y = -3/2 x + 2` `y = 3/2 x + 2` `y = -2/3 x + 2` `y = 2/3 x + 2`
 
 
 
 
Show Answers Only

`y = 3/2 x + 2`

Show Worked Solution

`text(Solution 1)`

`text(Graph cuts)\ y text(-axis at 2)`

`text(Gradient) = text(rise)/text(run) = 3/2`

`:. y = 3/2 x + 2`

 

`text(Solution 2)`

`text(Graph passes through)\ (2, 5) and (-2, -1)`

`text(By trial and error:)`

`text(Input each point into option 2’s equation,)`

`5 = 3/2 xx 2 + 2 = 5` ✔

`-1 = 3/2 xx – 2 + 2 = -1` ✔

 
`:. y = 3/2 x + 2\ \ text(is the equation of the line.)“

Algebra, NAP-K4-CA21

Wendy went to the supermarket to buy milk, soup, pineapple and cereal.

The pineapple cost half as much as the cereal.

The cost of different combinations of her items is shown below.
 

 
What is the cost of the milk?

$1 $1.50 $2 $2.50
 
 
 
 
Show Answers Only

`$2`

Show Worked Solution

`text(S)text(ince pineapple)\ (p) = 1/2\ text(cereal)\ (c)`

`c` `= 2p`
`2p+p` `= 7.50`
`p` `= $2.50`

 

`m + s + p + c` `= 13`
`m + 6 + 5` `= 13`
`m` `= $2`

 
`:.\ text(Milk costs)\ $2`

Statistics, NAP-E3-NC29 SA

Melinda and Cathy run the 100 metre sprint in their school athletics carnival.

A device tracks their progress and the results are graphed below.
 

 
Melinda starts quickly and passes the 75 metre mark after 10 seconds, slowing down as the race progresses.

Cathy is slower but runs the whole race at the same speed.

How long after Melinda did Cathy pass the 75 metre mark in the race?

    seconds
Show Answers Only

`5`

Show Worked Solution

`text(Melinda passes 75 metre mark at 10 seconds.)`

`text(Cathy passes at 15 seconds.)`

`:.\ text(Cathy passes 5 seconds after Melinda.)`

Geometry, NAP-G3-NC25 SA

This drawing shows how a large rectangular prism is cut into 3 objects.

Step 1: A medium rectangular prism is cut from a large rectangular prism.
 

 
Step 2: The smaller rectangular prism is cut into 2 identical triangular prisms.

What is the total number of faces of the three pieces after Step 2, including the bases?

    faces
Show Answers Only

`19`

Show Worked Solution

`text(Faces on triangular prism = 5)`

`text{Faces on larger rectangle (after step 1) = 9}`

`:.\ text(Total faces of 3 shapes)`

`= (2 xx 5) + 9`

`= 19`

Number, NAP-A3-NC26 SA

This picture shows the length of three shot put throws at a school athletics carnival.

Shot put 2 lands exactly halfway between shot put 1 and shot put 3.
 

 

 
What is the distance between the throw line and shot put 2?
Show Answers Only

`6.0\ text(metres)`

Show Worked Solution

`text(Difference between shot put 1 and 3)`

`= 6.9 – 5.1`

`= 1.8\ text(m)`
 

`:.\ text(Distance from throw line to shot put 2)`

`= 5.1 + 0.5 xx 1.8`

`= 6.0\ text(metres)`