smc-814-50-Loan Graphs

Financial Maths, STD2 F4 SM-Bank 1 MC

Ernie took out a reducing balance loan to buy a new family home.

He correctly graphed the amount paid off the principal of his loan each year for the first five years.

The shape of this graph (for the first five years of the loan) is best represented by

Show Answers Only

`B`

Show Worked Solution

`text(A reducing balance loan means that the amount of)`

`text(interest paid out decreases each year, and therefore)`

`text(the amount paid off the principal will not only increase)`

`text(each year, but will do so at an increasing rate.)`

`B\ text(correctly shows this trend.)`

`=> B`

Financial Maths, STD2 F4 2015 HSC 29b

Jamal borrowed $350 000 to be repaid over 30 years, with monthly repayments of $1880. However, after 10 years he made a lump sum payment of $80 000. The monthly repayment remained unchanged. The graph shows the balances owing over the period of the loan.

Over the period of the loan, how much less did Jamal pay by making the lump sum payment? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`$100\ 480`

Show Worked Solution

`text(Without the lump sum payment)`

♦ Mean mark 34%.

`text(Total repayments)`	`= 30 xx 12 xx $1880`
	`= $676\ 800`

`text(With the lump sum payment)`

`text(Total repayments)`	`= (22 xx 12 xx $1880) + $80\ 000`
	`= $496\ 320 + $80\ 000`
	`= $576\ 320`

`:.\ text(Amount Jamal saved)`

`= 676\ 800 − 576\ 230`

`= $100\ 480`

Financial Maths, STD2 F4 2010 HSC 28a

The table shows monthly home loan repayments with interest rate changes from February to October 2009.

What is the change in monthly repayments on a $250 000 loan from February 2009 to April 2009? (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Xiang wants to borrow $307 000 to buy a house.

Xiang’s bank approves loans for customers if their loan repayments are no more than 30% of their monthly gross salary.

Xiang’s monthly gross salary is $6500.

If she had applied for the loan in October 2009, would her bank have approved her loan?

Justify your answer with suitable calculations. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Jack took out a loan at the same time and for the same amount as Xiang.

Graphs of their loan balances are shown.

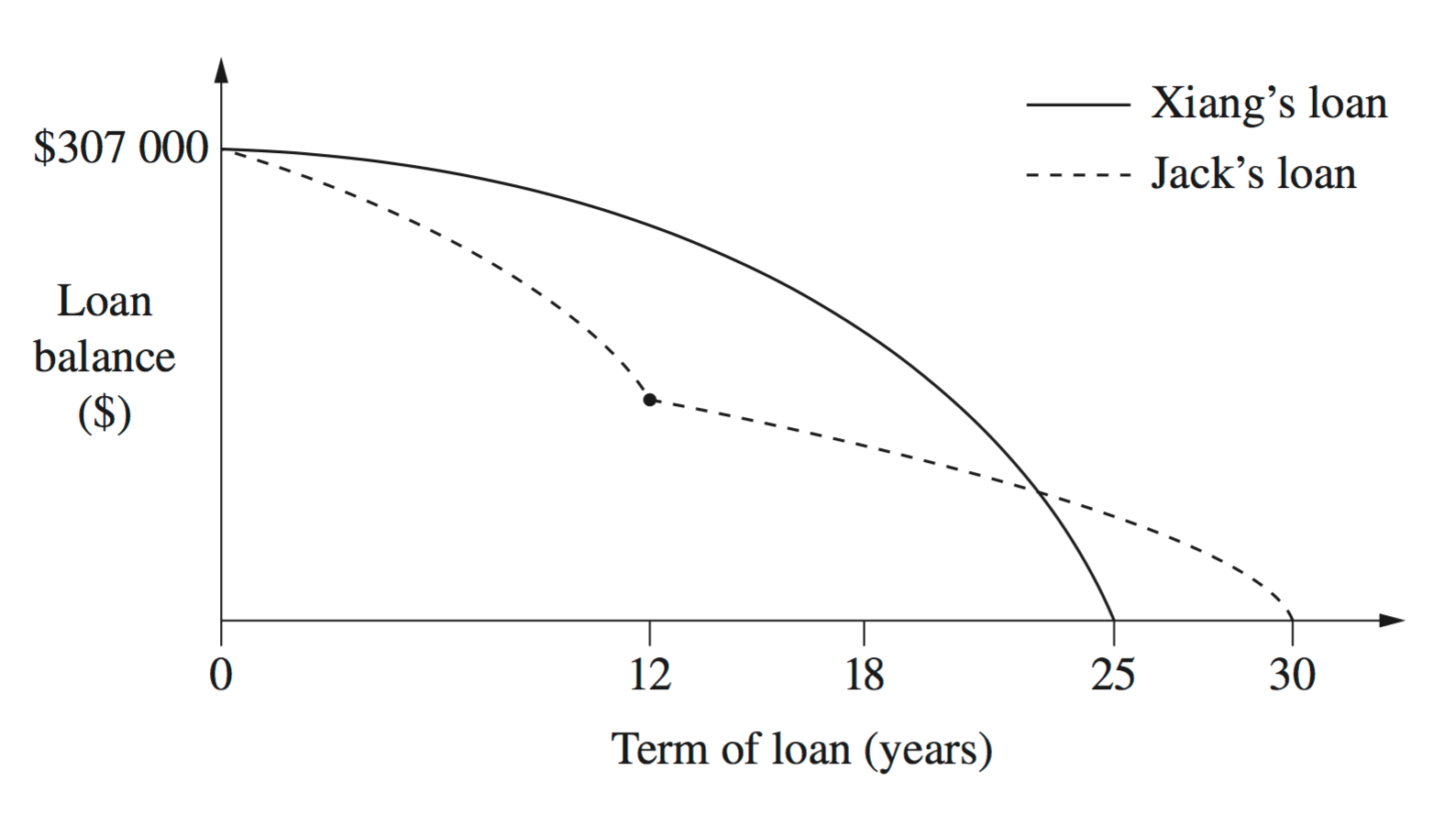
Identify TWO differences between the graphs and provide a possible explanation for each difference, making reference to interest rates and/or loan repayments. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Monthly repayments decrease by $15)`
`text(S)text(ince repayments of 1987.29 > 1950, the loan)`
`text(would not have been approved.)`
`text(Differences)`
`text(Jack’s loan balance falls more sharply for first 12 years)`
`text(Jack’s loan balance falls less sharply between years 12-30.)`
`text(Explanation)`
`text(Jack made larger repayments for first 12 years, or)`
`text(Jack made the same repayments but had a lower interest rate)`
`text(for the first 12 years.)`
`text(Jack made smaller repayments in years 12-30.)`

Show Worked Solution

i.	`text(Repayment)\ text{(Feb 09)}`	`= 1588`
	`text(Repayment)\ text{(Apr 09)}`	`= 1573`

`text(Difference) = 1588\-1573 = 15`

`:.\ text(Monthly repayments decrease by $15)`

♦ Mean mark 39%
MARKER’S COMMENT: Borrowing $307,000 can be achieved by borrowing $300,000, and then `7` times the table repayment value for borrowing $1000.

ii.

`text(Loan) = $307\ 000`

`text{Repayments (Oct 09)}`	`= 1942 + (7 xx 6.47)`
	`= 1942 + 45.29`
	`= $1987.29\ text(per month)`

`text(30% Gross salary)`	`= 6500 xx\ text(30%)`
	`= $1950\ text(per month)`

`:.\ text(S)text(ince repayments of $1987.29 > $1950, the loan)`

`text(would not have been approved.)`

iii. `text(Differences)`

`text(Jack’s loan balance falls more sharply for first 12 years)`

`text(Jack’s loan balance falls less sharply between years 12-30.)`

`text{Explanation(s)}`

♦ Mean mark 36%
MARKER’S COMMENT: Explanations were generally poor and many failed to refer directly to the graphs shown, or reference Xiang or Jack directly.

`text(Jack made larger repayments for 1st 12 years, or)`

`text(Jack made the same repayments but had a)`

`text(lower interest rate for the first 12 years.)`

`text(Jack made smaller repayments in years 12-30.)`

Financial Maths, STD2 F4 2012 HSC 24 MC

A $400 000 loan can be repaid by making either monthly or fortnightly repayments.

The graph shows the loan balances over time using these two different methods of repayment.

The monthly repayment is $2796.86 and the fortnightly repayment is $1404.76.

What is the difference in the total interest paid using the two different methods of
repayment, to the nearest dollar?

$51 596
$166 823
$210 000
$234 936

Show Answers Only

`B`

Show Worked Solution

`text(Monthly repayment)`	`= $2796.86`
`text(# Repayments)`	`= 30 xx 12 = 360`
`text(Total repaid)`	`= 360 xx 2796.86`
	`= $1\ 006\ 869.60`
`text(Total interest)`	`= 1\ 006\ 869.60\ -400\ 000`
	`=$606\ 869.60`

`text(Fortnightly payment)`	`= $1404.76`
`text(# Repayments)`	`= 23 xx 26 = 598`
`text(Total repaid)`	`= 598 xx 1404.76`
	`=$840\ 046.48`
`text(Total interest)`	`= 840\ 046.48-400\ 000`
	`= $440\ 046.48`

`:.\ text(Difference in interest)`	`= 606\ 869.60-440\ 046.48`
	`= $166\ 823\ \ \ text((nearest dollar))`

`=> B`