SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Algebra, STD2 A4 2013 HSC 30a

Wind turbines, such as those shown, are used to generate power.

2013 30a

In theory, the power that could be generated by a wind turbine is modelled using the equation

`T = 20\ 000w^3`

where `T` is the theoretical power generated, in watts 
  `w` is the speed of the wind, in metres per second.

 

  1. Using this equation, what is the theoretical power generated by a wind turbine if the wind speed is 7.3 m/s ?  (1 mark)

In practice, the actual power generated by a wind turbine is only 40% of the theoretical power.

  1. If `A` is the actual power generated, in watts, write an equation for `A` in terms of `w`.    (1 mark)

The graph shows both the theoretical power generated and the actual power generated by a particular wind turbine.
 
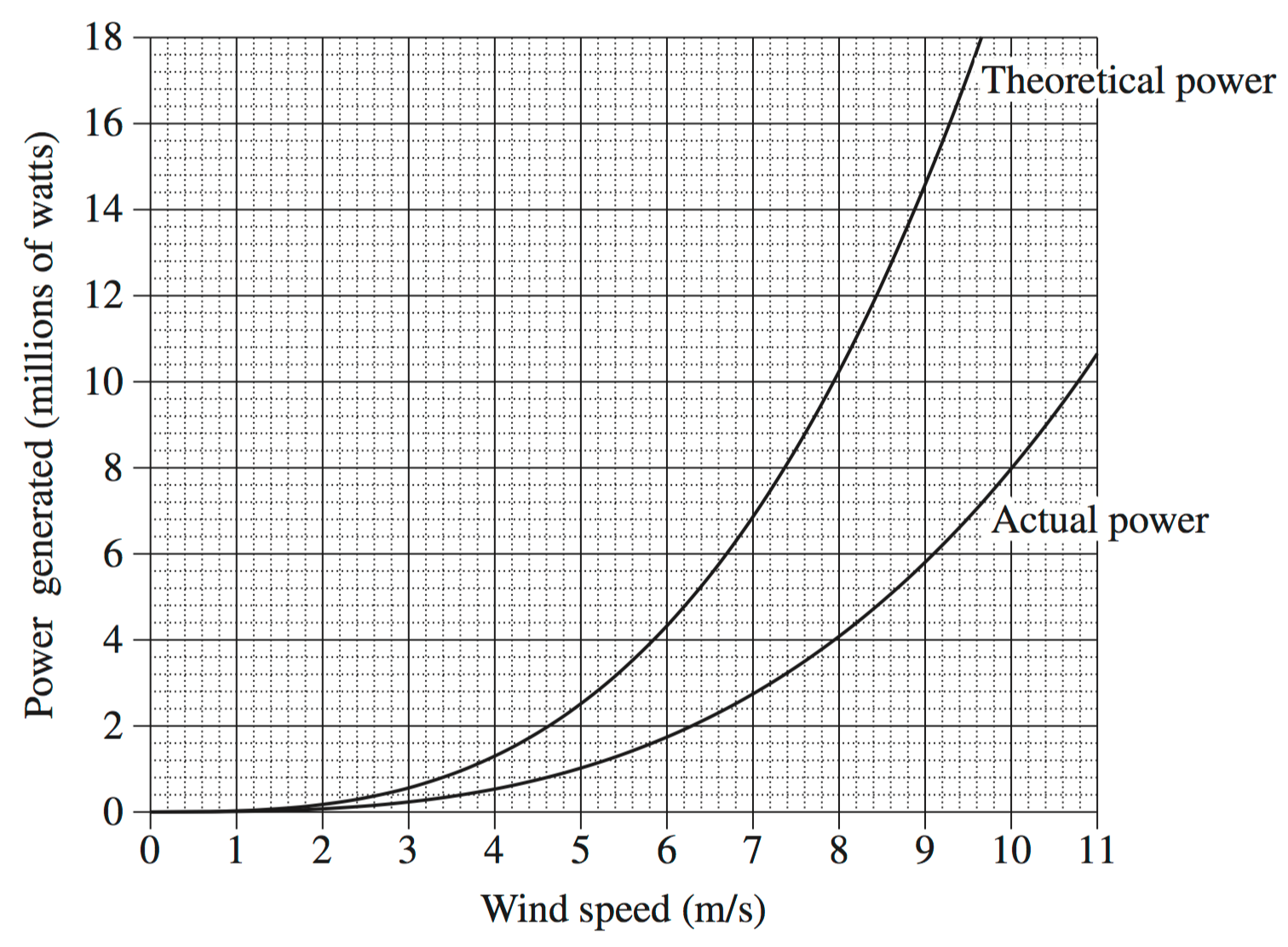
        2013 30a2

  1. Using the graph, or otherwise, find the difference between the theoretical power and the actual power generated when the wind speed is 9 m/s.   (1 mark)

A particular farm requires at least 4.4 million watts of actual power in order to be self-sufficient.

  1. What is the minimum wind speed required for the farm to be self-sufficient?    (1 mark)

A more accurate formula to calculate the power (`P`) generated by a wind turbine is

`P = 0.61 xx pi xx r^2 × w^3` 

where     `r` is the length of each blade, in metres
  `w` is the speed of the wind, in metres per second. 

 
Each blade of a particular wind turbine has a length of 43 metres.The turbine operates at a wind speed of 8 m/s.

  1. Using the formula above, if the wind speed increased by 10%, what would be the percentage increase in the power generated by this wind turbine?   (3 marks)

Show Answers Only
  1. `7\ 780\ 340\ text(watts)`
  2. `8000w^3`
  3. `8.8\ text(million watts, or 8 748 000 watts)`
  4. `w = 8.2\ text(m/s)\ \ \ text{(1 d.p.)}`
  5. `text(33%)`
Show Worked Solution
i.    `T=20\ 000w^3`
  `text(If)\ \ w = 7.3`
`T` `=20\ 000 xx (7.3)^3`
  `= 7\ 780\ 340\ text(watts)`

  

♦ Mean mark 34%
ii.    `text(We know)\ A = 40% xx T`
`=> A` `=0.4 xx 20\ 000 xx w^3`
  `=8000w^3`

  

♦ Mean mark 38%
iii.    `text(Solution 1)`
  `text(At)\ w=9`
  `A = text(5.8 million watts)\ \ \ text{(from graph)}`
  `T = text(14.6 million watts)\ \ \ text{(from graph)}`
`text(Difference)` `= text(14.6 million)\-text(5.8 million)`
  `= text(8.8 million watts)`

 

`text(Alternative Solution)`
`text(At)\ w=9`
`T` `= 20\ 000 xx 9^3`
  `= 14\ 580\ 000\ text(watts)`
`A` `= 8000 xx 9^3`
  `= 5\ 832\ 000\ text(watts)`
`text(Difference)` `=14\ 580\ 000\-5\ 832\ 000`
  `=8\ 748\ 000\ \ text(watts)`

  

♦♦ Mean mark 25%
COMMENT: Students need to be comfortable in finding the cube roots of values – a calculation that can be required in a number of topic areas and is regularly examined.
iv.    `text(Find)\ w\ text(if)\ A=4.4\ text(million)`
`8000w^3` `= 4\ 400\ 000`
`w^3` `= (4\ 400\ 000)/8000`
  `= 550`
`:. w` `= root(3)(550)`
  `=8.1932…`
  `=8.2\ text(m/s)\ \ \ text{(1 d.p.)}`

 

`:.\ text(The minimum wind speed required is 8.2 m/s)`

 

♦ Mean mark 41%
MARKER’S COMMENT: Students are reminded that a % increase requires them to find the difference in power generated at different wind speeds and divide this result by the original power output, as shown in the Worked Solution.
v.    `text(Find)\ P\ text(when)\ w=8\ text(and)\ r=43`
`P` `= 0.61 xx pi xx r^2 xx w^3`
  `= 0.61 xx pi xx 43^2 xx 8^3`
  `= 1\ 814\ 205.92\ text(watts)`

 

`text(When speed of wind)\ uarr10%`
`w′ = 8 xx 110text(%) = 8.8\ text(m/s)`
 

`text(Find)\ P\ text(when)\ w′ = 8.8`

`P` `=0.61 xx pi xx 43^2 xx 8.8^3`
  `= 2\ 414\ 708.08\ text(watts)`

 

`text(Increase in Power)` `=2\ 414\ 708.08\-1\ 814\ 205.92`
  `= 600\ 502.16`

 

`:.\ text(% Power increase)` `= (600\ 502.16)/(1\ 814\ 205.92)`
  `= 0.331`
  `= text(33%)\ \ \ text{(nearest %)}`