SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, SMB-015 MC

Consider the following four statements about the graph above:

    • The graph is planar.
    • The graph contains a cycle.
    • The graph is connected.
    • The graph contains an Eulerian trail.

How many of these statements are true?

  1. 1
  2. 2
  3. 3
  4. 4
Show Answers Only

`C`

Show Worked Solution

`text{Consider each statement:}`

`text{Graph is planar}\ -> \text{edges only meet at vertices (True)}` 

`text{Graph contains a cycle}\ -> \text{multiple cycles exist (True)}`

`text{Graph is connected}\ -> \text{a path exists to connect any}`

`text{two vertices (True)}`

`text{Graph contains an Eulerian trail}\ -> \text{requires two (only)}`

`text{vertices of an odd degree (False)}`

`=> C`

Networks, SMB-014 MC

An Eulerian trail for the graph above will be possible if only one edge is removed.

In how many different ways could this be done?

  1. `2`
  2. `3`
  3. `4`
  4. `5`
Show Answers Only

`D`

Show Worked Solution

`text{Konigsberg: an Eulerian trail needs two vertices (only) to have}`

`text{an odd degree.}`

`text{The graph has 4 vertices that are odd degree.}`

`text{Removing any of the dashed edges below would achieve this.}`
 

`=> D`

Networks, SMB-013 MC

Consider the graph below.

The minimum number of extra edges that are required so that an Eulerian trail is possible in this graph is

  1. 0
  2. 1
  3. 2
  4. 3
Show Answers Only

`B`

Show Worked Solution

`\text{Eulerian trail – every edge is used once only.}`
 

`text{Eulerian trails allow two vertices (only) to be odd.}`

`:.\ text{Need 1 extra edge that creates two even degree vertices (see image).}`

`=>  B`

Networks, SMB-012

A network diagram is drawn below.
 

  1. Starting at vertex `Z`, identify a trail that uses 6 edges and ends at vertex `V`.   (1 mark)

  2. Starting at vertex `V`, identify all six different paths that end at vertex `Y`.   (2 marks)

  3. Is the route identified as `YXUVXY` a circuit? Explain.  (1 mark)

Show Answers Only

i.    `text{Trail: repeated vertices permitted but no repeated edges}`

`text{Trail (6 edges)}\ Z–V:`

`ZWXYUXV\ \ \text{or}\ \ ZWXUYXV` 
 

ii.    `text{Path: a route that does not repeat vertices or edges.}`

`text{Possible paths}\ V–Y:`

`VUY, VUXY, VUXWZY`

`VXUY, VXY, VXWZY`
 

iii.   `text{Circuit: starts and ends at the same vertex with repeated}`

`text{vertices allowed but no repeated edges.}`

`YXUVXY\ \text{is not a circuit because it edge}\ XY\ \text{is repeated.}`

Show Worked Solution

i.    `text{Trail: repeated vertices permitted but no repeated edges}`

`text{Trail (6 edges)}\ Z–V:`

`ZWXYUXV\ \ \text{or}\ \ ZWXUYXV`
 

ii.    `text{Path: a route that does not repeat vertices or edges.}`

`text{Possible paths}\ V–Y:`

`VUY, VUXY, VUXWZY`

`VXUY, VXY, VXWZY`
 

iii.   `text{Circuit: starts and ends at the same vertex with repeated}`

`text{vertices allowed but no repeated edges.}`

`YXUVXY\ \text{is not a circuit because it edge}\ XY\ \text{is repeated.}`

Networks, SMB-011

A network diagram is drawn below.
 

  1. Starting at vertex `Q`, identify all five different paths that end at vertex `S`.   (2 marks)

  2. Starting at vertex `P`, identify four different cycles that exist in the network.   (2 marks)

  3. Starting at vertex `P`, what is the total number of cycles that exist in the network.  (1 mark)

Show Answers Only

i.    `text{Paths from}\ Q–S:`

`QS, QRS, QRPS, QPRS, QPS`
 

ii.    `text{Cycle: a path that ends at the same vertex without}`

`text{repeating any vertices.}`

`text{Possible cycles (any 4 from the following):}`

`PQRP, PQSRP, PQRSP, PQSP, PSRP`

`PSRQP, PSQRP, PSQP`
 

iii.  `8\ \text{(see listed in part (ii))}`

Show Worked Solution

i.    `text{Paths from}\ Q–S:`

`QS, QRS, QRPS, QPRS, QPS`
 

ii.    `text{Cycle: a path that ends at the same vertex without}`

`text{repeating any vertices.}`

`text{Possible cycles (any 4 from the following):}`

`PQRP, PQSRP, PQRSP, PQSP, PSRP`

`PSRQP, PSQRP, PSQP`
 

iii.  `8\ \text{(see listed in part (ii))}`

Networks, SMB-010

  1. Starting at vertex `A`, identify all the different paths that finish at vertex `D`, using only three edges.   (2 marks)

  2. Starting at vertex `A`, identify a cycle route?   (1 mark)

  3. Explain the difference between a cycle and a circuit route.   (1 mark)

Show Answers Only

i.    `text{Three edge paths from}\ A–D:`

`ACED, ABCD, ABED, AECD`

ii.    `text{Cycle: a path that ends at the same vertex without}`

`text{repeating any.}`

`text{Possible cycles (many examples exist in this network):}`

`ABEA, ABCEA, ACBA, …`

iii.  `text{A circuit is a path that begins and ends at the same vertex.}`

`text{A cycle begins and ends at the same vertex, without}`

`text{repeating any vertices.}`

Show Worked Solution

i.    `text{Three edge paths from}\ A–D:`

`ACED, ABCD, ABED, AECD`
 

ii.    `text{Cycle: a path that ends at the same vertex without}`

`text{repeating any.}`

`text{Possible cycles (many examples exist in this network):}`

`ABEA, ABCEA, ACBA, …`
 

iii.  `text{A circuit is a path that begins and ends at the same vertex.}`

`text{A cycle begins and ends at the same vertex, without}`

`text{repeating any vertices.}`

Networks, SMB-009

  1. Starting at vertex `A`, identify three different cycles in the above network.   (2 marks)

  2. Starting at vertex `A`, how many different cycles exist in this network?   (1 mark)

Show Answers Only

i.    `text{Possible cycles (select 3):}`

`ABECA, ABEDA, ACEBA, ACEDA, ADEBA, ADECA`

ii.    `text{6 (see above)}`

Show Worked Solution

i.    `text{Cycle definition: edges cannot be repeated, only first and last}`

`text{vertices can be be repeated.}`

`:.\ text{Possible cycles (select 3):}`

`ABECA, ABEDA, ACEBA, ACEDA, ADEBA, ADECA`

ii.    `text{6 (see above)}`

Networks, SMB-008

The diagram below shows a network of train lines between five towns: Attard, Bower, Clement, Derrin and Eden.

The numbers indicate the distances, in kilometres, that are travelled by train between connected towns.
 

 

Charlie followed an Eulerian trail through this network of train lines.

  1. Write down the names of the towns at the start and at the end of Charlie’s trail.  (1 mark)
  2. What distance did he travel?  (2 marks)
Show Answers Only
  1. `text(Bower, Eden)`
  2. `910\ text(km)`
Show Worked Solution

i.   `text{Eulerian trail starts and ends at odd degree vertices (towns).}`

`text(Bower, Eden or Eden, Bower)`

 
ii.   `text{Eulerian trail}\ =>\ text{every edge used once only.}`

`text{Distance}\ (BDABCDEACE)`

`= 160 + 130 + 80 + 70 + 60 + 40 + 100 + 150 + 120`

`= 910\ text(km)`

Networks, SMB-007

The city of Robville contains eight landmarks denoted as vertices `N` to `U` on the network diagram below. The edges on this network represent the roads that link the eight landmarks.
 

  

  1. Write down the degree of vertex `U`.  (1 mark)

  2. Steven wants to visit each landmark, but drive along each road only once. He will begin his journey at landmark `N`.
  3. At which landmark must he finish his journey?  (1 mark)

  4. Regardless of which route Steven decides to take, how many of the landmarks (including those at the start and finish) will he see on exactly two occasions?  (2 marks)

Show Answers Only
  1. `4`
  2. `P\ text{(the other odd degree vertex)}`
  3. `5`
Show Worked Solution

i.   `4`
 

ii.   `P\ text{(the other odd degree vertex)}`

`text{(The Konigsberg Bridge concept is used here)}`
 

iii.   `text{Any vertex (landmark) with a degree of 3 or 4 will be seen twice.}`

`5 (N, T, R, P, U)`

Networks, SMB-006

In one area of the town of Zenith, a postal worker delivers mail to 10 houses labelled as vertices `A` to `J` on the graph below.
 

  1. Which one of the vertices on the graph has degree 4?  (1 mark)

For this graph, an Eulerian trail does not currently exist.

  1. For an Eulerian trail to exist, what is the minimum number of extra edges that the graph would require, giving reasons.  (2 marks)

Show Answers Only
  1. `text(Vertex)\ F`
  2. `2`
Show Worked Solution

i.    `text(Vertex)\ F`
 

ii.   `text(Eulerian trail)\ =>\ text(all edges used exactly once.)`

`text(6 vertices are odd)`

`text{Konigsberg Bridge concept: Eulerian trail can exist if 2 vertices (only) are odd}`

`=>\ text(2 extra edges could create graph with only 2 odd vertices)`

`:.\ text(Minimum of 2 extra edges.)`

Networks, SMB-005

The vertices in the network diagram below show the entrance to a wildlife park and six picnic areas in the park: `P1`, `P2`, `P3`, `P4`, `P5` and `P6`.

The numbers on the edges represent the lengths, in metres, of the roads joining these locations.

 

  1. In this graph, what is the degree of the vertex at the entrance to the wildlife park?  (1 mark)

  2. What is the shortest distance, in metres, from the entrance to picnic area `P3`?  (1 mark)

A park ranger starts at the entrance and drives along every road in the park once.

  1. At which picnic area will the park ranger finish?  (2 marks)

  2. What mathematical term is used to describe the route the park ranger takes?  (1 mark)

Show Answers Only
  1. `3`
  2. `1000\ text(m)`
  3. `P4`
  4. `text(Euler trail)`
Show Worked Solution

i.   `3`
 

ii.   `text( Shortest distance)`

`= E-P1-P3`

`= 600 + 400`

`= 1000\ text(m)`
 

iii.   `text(A route could be)`

`E − P1 − P2 − P3 − P4 − P5`

`− E − P6 − P1 − P3 − P6 − P4`

`:.\ text(Finish at)\ P4`

`text{(Konigsberg bridge – Eulerian trail ends at the only other}`

`text{odd degree vertex)}`
 

iv.   `text(Eulerian trail)`

Networks, SMB-004

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.
 

  1. In kilometres, what is the shortest distance between Farnham and Carrie?  (1 mark)

  2. How many different paths are there to travel from Farnham to Carrie without passing through any town more than once?  (1 mark)

An engineer plans to inspect all of the roads in this network.

He will start at Dunlop and inspect each road only once.

  1. At which town will the inspection finish?  (2 marks)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
  3. `text(Bredon)`
Show Worked Solution

i.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`

 

ii.   `text{Paths are walks where vertices and edges are only used once.}`

`text(Different paths are:)`

`FDC, FEDC, FEBC, FEABC, FDEBC, FDEABC`

`:. 6\ text(different ways)`

 

iii.   `text(A possible path is)\ DFEABCDEB\ text(and will finish)`

`text{at Bredon.}`

`text{Note: solving this can be done quickly by applying the}`

`text{concept underlying the Konigsberg Bridge problem}`

`text{(i.e. it finishes at the only other odd-degree vertex)}`

Networks, SMB-003

The following network diagram has a Eulerian trail. 
 

Starting at vertex `D`, describe one Eulerian trail and at what vertex the trail finishes.  (2 marks)

Show Answers Only

`text{Possible trails:}`

`DACEBD, DBECAD`

`text{All Eulerian trails will finish at vertex}\ D.`

Show Worked Solution

`text{Possible trails:}`

`DACEBD, DBECAD`

`text{All Eulerian trails will finish at vertex}\ D.`

Networks, SMB-002

The following network diagram shows the distances, in kilometres, along the roads that connect six intersections `A`, `B`, `C`, `D`, `E` and `F`.
 

  1. A cyclist started at intersection `D` and cycled along every road in this network once only. What route would the cyclist take and at which intersection would she finish?  (3 marks)

  2. What is another name for this type of trail?   (1 mark)

Show Answers Only

i.   `text{Possible trails:}`

`DEFDCBFAB, DEFDCBAFB,`

`DEFBAFDCB, DEFABFDCB`

`text{All routes finish at intersection}\ B.`
 

ii.   `text{Eulerian trail}`

Show Worked Solution

i.   `text{Possible trails:}`

`DEFDCBFAB, DEFDCBAFB,`

`DEFBAFDCB, DEFABFDCB`

`text{All routes finish at intersection}\ B.`
 

ii.   `text{Eulerian trail}`

Networks, SMB-001

The network diagram below describes a skateboard park with seven ramps.

The ramps are shown as vertices `T`, `U`, `V`, `W`, `X`, `Y` and `Z` on the graph below.
 

 

The tracks between ramps `U` and `V` and between ramps `W` and `X` are rough, and cannot be used by skateboards.

  1. Describe a path that a skateboarder at ramp `V` could use to travel to ramp `T` that uses 4 edges only.   (1 mark)

  2. A skateboarder begins skating at ramp `W` and follows an Eulerian trail.
  3. What trail does the skateboarder take?  (2 marks)

Show Answers Only
  1. `text{Possible paths:}\ \ VZYT, VZUT`
  2. `XYZWVZUYTU\ \ \text{(Finishes at ramp}\ U\text{)}`
Show Worked Solution

i.    `text{Possible paths:}\ \ VZYT, VZUT, VZYUT`

 
ii.    `text{The Eulerian trail (visits each edge exactly once):}`

`XYZWVZUYTU`

Networks, SMB-023

A new housing estate is being developed.

There are five houses under construction in one location.

These houses are numbered as points 1 to 5 below.
 

  
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.

  1. What is the minimum number of edges needed to connect the five houses?  (1 mark)

  2. On the diagram above, draw a connected graph with this number of edges.  (1 mark) 

Show Answers Only

i.   `text(Minimum number of edges = 4)`
 

ii.   `text(One of many possibilities:)`
 

Show Worked Solution

i.   `text(Minimum number of edges = 4)`
 

ii.   `text(One of many possibilities:)`
 

Networks, SMB-022

The following graph with five vertices is a complete graph.
 

How many edges must be removed so that the graph will have the minimum number of edges to remain connected. Explain your answer.   (3 marks)

Show Answers Only

`text{6 edges need to be removed}`

Show Worked Solution

`text(The minimum number of edges for a connected graph with)`

`text{5 vertices is 4 (see one possible example below).}`
 

 
`:.\ text(Edges to be removed)\ = 10-4= 6`

Networks, SMB-021

Consider the following graph.
 

On the diagram above, make this a connected graph, using the smallest number of edges.   (2 marks)

Show Answers Only

`text{Any addition of 3 edges that connects all vertices.}`
 

Show Worked Solution

`text{Any addition of 3 edges that connects all vertices.}`
 

Networks, SMB-019

The network below can be represented as a planar graph.
 

Redraw the graph as a planar representation of the network, labelling each vertex.   (2 marks)

Show Answers Only

Show Worked Solution

`text{Redrawing the graph in planar form (no edges crossing):}` 
 

Networks, SMB-018

The network below can be represented as a planar graph.

 

Redraw the graph as a planar representation of the network, labelling each vertex.   (2 marks)

Show Answers Only

Show Worked Solution

`text{Redrawing the graph in planar form (no edges crossing):}` 
 

Networks, SMB-020 MC

The graph above has

  1. 5 faces.
  2. 6 faces.
  3. 8 faces.
  4. 9 faces.
Show Answers Only

`=> B`

Show Worked Solution

`text(Redrawing the graph in planar form,)`

`text(the graph can be seen to have 6 faces.)`
 

`text(Alternatively, using Euler’s rule:)`

`v + f` `= e + 2`
`5 + f` `= 9 + 2`
`:. f` `= 6`

 
`=> B`

Networks, SMB-017

The network below can be represented as a planar graph.
 

Redraw the graph as a planar representation of the network, labelling each vertex.   (2 marks)

Show Answers Only

Show Worked Solution

`text{Redrawing the graph in planar form (no edges crossing):}` 
 

Networks, SMB-016

The network below can be represented as a planar graph.
 

Complete the partial graph drawn below, adding the missing edges so that it is a planar representation of the above network.   (3 marks)
  

Show Answers Only

Show Worked Solution

`text{Redrawing the graph in planar form (no edges crossing):}` 
 

Networks, SMB-015

The network below can be represented as a planar graph.
 

Draw the planar graph representation of this network, labelling each vertex.   (2 marks)

Show Answers Only

Show Worked Solution

`text{Redrawing the graph in planar form (no edges crossing):}` 
 

`text{Each vertex is the same degree as the original graph and}`

`text{has edges connecting to the same vertices.}`

Networks, SMB-014

The network below can be represented as a planar graph.
 

Draw the planar graph representation of this network and find the number of faces in the planar graph.   (3 marks)

Show Answers Only

`text{Number of faces = 6}`

Show Worked Solution

`text(Redrawing the graph in planar form:)` 

`text{Method 1}`

`text{Number of faces = 6 (by inspection)}`

 
`text(Method 2 (Euler’s formula))`

`v + f` `= e + 2`
`5 + f` `= 9 + 2`
`:. f` `= 6`

Networks, SMB-013

Consider the planar graph below.
 

 
Euler’s formula will be verified for this graph.

Find the values of `e, v` and `f` and use them to verify Euler's formula.   (3 marks)

Show Answers Only

`e=6, v=5, f=3`

Show Worked Solution

`text{Number of edges:}\ e=6`

`text{Number of vertices:}\ v=5`

`text{Number of faces:}\ f=3`

`text(Verifying Euler’s formula):\ \ v + f = e + 2`

`5+3` `= 6+2`
`8` `= 8\ \ =>\ \text{Euler holds}`

Networks, SMB-012

A connected planar graph has 4 edges and 4 faces.

  1. Calculate the number of vertices for this graph.  (2 marks)
  2. Draw the planar graph.   (2 marks)
Show Answers Only

i.    `text{2 vertices}`

ii.    
         

Show Worked Solution
i.    `v+f` `=e+2`
`:. v` `=e-f + 2`
  `= 4-4 + 2`
  `= 2`

 
ii.   
           

Networks, SMB-009 MC

A planar graph has five faces.

This graph could have

  1.  six vertices and eight edges.
  2.  eight vertices and five edges.
  3.  eight vertices and six edges.
  4.  five vertices and eight edges.
Show Answers Only

`D`

Show Worked Solution

`text(Using Euler’s formula:)`

`v + f` `= e + 2`
`v + 5` `= e + 2`
`v + 3` `= e`

 
`text{Consider each option:}`

`text{5 vertices and 8 edges → Euler holds}`

`=> D`

Networks, SMB-007 MC

A connected planar graph has 12 edges.

This graph could have

  1. 5 vertices and 6 faces.
  2. 5 vertices and 8 faces.
  3. 6 vertices and 8 faces.
  4. 6 vertices and 9 faces.
Show Answers Only

`C`

Show Worked Solution

`text(Consider option C:)`

`v + f` `= e + 2`
`6 + 8` `= 12 + 2`
`14` `= 14`

 

 
`text(i.e. Euler’s formula holds.)`

`=>  C`

Networks, SMB-006

Consider the graph below.
 

  1. Redraw this network as a planar graph.   (1 mark)

  2. Find the number of faces on the planar graph.   (2 marks)

Show Answers Only

i.   
       

 
ii.    \(\text{Number of faces = 4}\)

Show Worked Solution

i.   
       

 
ii.    \(\text{Method 1}\)

\(\text{By inspection, number of faces = 4}\)
 

\(\text{Method 2}\)

`v-e+f` `=2`  
`4-6+f` `=2`  
`f` `=4`  

Networks, SMB-005

A network is represented by the following graph.
 

  1. Draw the above network as a planar graph.   (1 mark)
  2. Find the number of faces of this planar graph.   (2 marks)
Show Answers Only

i.    
       

ii.    \(6\)

Show Worked Solution

i.    
       

 
ii.    \(\text{Method 1}\)

\(\text{By inspection (see image above):} \)

\(\text{Number of faces = 6} \)
 

\(\text{Method 2}\)

`v-e+f` `=2`  
`8-12+f` `=2`  
`f` `=6`  

Circle Geometry, SMB-019

The diagram shows a large semicircle with diameter  `AB`  and two smaller semicircles with diameters  `AC`  and  `BC`, respectively, where  `C`  is a point on the diameter  `AB`. The point  `M`  is the centre of the semicircle with diameter  `AC`.

The line perpendicular to  `AB`  through  `C`  meets the largest semicircle at the point  `D`. The points  `S`  and  `T`  are the intersections of the lines  `AD`  and  `BD`  with the smaller semicircles. The point  `X`  is the intersection of the lines  `CD`  and  `ST`.
 

Explain why `CTDS` is a rectangle.   (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

`/_SDT = 90°\ text{(angle in semi-circle)}`

`/_ ASC = 90°\ \ text{(angle in semi-circle)}`

`=> /_ CSD = 180-90=90°\ \ text{(} /_ ASD\ text{is a straight line)}`

`text(Similarly,)`

`/_CTB = /_CTD=90°`

`/_SCT = 90°\ \ text{(angle sum of quadrilateral}\ CTDS text{)}`

`text(S)text(ince all angles are right angles,)`

`CTDS\ text(is a rectangle)` 

Circle Geometry, SMB-018

In the diagram, `AB` is a diameter of a circle with centre `O`. The point `C` is chosen such that `Delta ABC` is acute-angled. The circle intersects `AC` and `BC` at `P` and `Q` respectively.
 

Why is `/_BAC = /_CQP`?   (2 marks)

Show Answers Only

`text(Proof)\ text{(See Worked Solutions)}`

 

Show Worked Solution

`/_BAC + /_BQP = 180°\ \ (APQB\ text{is a cyclic quad})`

`/_CQP + /_BQP = 180°\ text{(}/_ CQB\ text{is a straight line)}`

`:.\ /_BAC = /_CQP`

Circle Geometry, SMB-017

In the diagram, the points `A`, `B`, `C` and `D` are on the circumference of a circle, whose centre `O` lies on `BD`. The chord `AC` intersects the diameter `BD` at `Y`. The tangent at `D` passes through the point `X`.

It is given that  `∠CYB = 100^@`  and  `∠DCY = 30^@`.

 

 

  1. What is the size of  `∠ACB`?   (1 mark)

  2. What is the size of  `∠CBD`?   (2 marks)

Show Answers Only
  1. `60^@`
  2. `20^@`
Show Worked Solution
i.    `∠DCB` `= 90^@\ \ text{(angle in semi-circle)}`
`∠ACB` `= 90-30`
  `= 60^@`

 
ii.    `∠CYD = 180-100=80^@\ \ text{(180° in straight line)}`

`∠CDY = 180-(80+30)=70^@\ \ text{(180° in Δ)}`

`∠CBD = 180-(90+70)=20^@\ \ text{(180° in Δ)}`

Circle Geometry, SMB-016

The line \(BD\) is a tangent to a circle and the secant \(AD\) intersects the circle at \(A\) and \(C\).
 

Given that  \(AC = 18\)  and  \(CD = 6\), find the value of \(x\).  (2 marks)   

Show Answers Only

\(x=12\)

Show Worked Solution
\(x^2\) \(= 6 \times (18 + 6) \)  
  \(=144\)  
\(x\) \(=12\)  

Circle Geometry, SMB-015

 

Find the size of angles \(x^{\circ}\) and \(y^{\circ}\).  (3 marks)   

Show Answers Only

\(x= 38^{\circ}\)

\(y= 104^{\circ}\)

Show Worked Solution

\(x=38^{\circ}\ \ \text{(angles standing on the same arc)} \)

\(\text{Let}\ \ \theta =\ \text{angle at centre on the same arc} \)

\(\theta = 2 \times 38 = 76^{\circ} \)

\(y^{\circ}\) \(=180-76\ \ \text{(180° in straight line)}\)  
  \(=104^{\circ} \)  

Circle Geometry, SMB-014

Find \(\angle ADC\).  (2 marks)   

Show Answers Only

\(x= 84^{\circ}\)

Show Worked Solution

\(\angle ABC = 180-105=75^{\circ}\ \ \text{(straight line)} \)

\(\angle ADC\) \(=180-75\ \ \text{(opposite angles of cyclic quad are supplementary)}\)  
  \(=105^{\circ} \)  

Circle Geometry, SMB-012

In the diagram, \(AC\) is a diameter of the circle centred \(O\), \(\angle BAC = 20^{\circ}\) and \(\angle CAD = 62^{\circ} \).
 

Find \(\angle BCD\).  (2 marks)   

Show Answers Only

\(\angle BCD= 98^{\circ}\)

Show Worked Solution

\( \angle BCD + \angle DAB = 180^{\circ} \ \ \text{(opposite angles of cyclic quad)} \)

\(\angle BCD\) \(=180-(62+20)\)  
  \(=98^{\circ} \)  

Circle Geometry, SMB-011

In the diagram, \(PR\) is a diameter of the circle centred \(O\) and \(\angle QPR = 15^{\circ} \).
 

Find \(\theta\).  (2 marks)   

Show Answers Only

\(\theta = 75^{\circ}\)

Show Worked Solution

\(\angle PQR = 90^{\circ}\ \  \text{(angle in semicircle)} \)

\(\theta\) \(=180-(90+15)\ \ (180^{\circ}\ \text{in}\ \Delta) \)  
  \(=75^{\circ} \)  

Circle Geometry, SMB-010

In the circle with centre at \(O\), \(\angle BAC = 36^{\circ}\).
 

Find \(\theta\).  (2 marks)   

Show Answers Only

\(\theta = 72^{\circ}\)

Show Worked Solution

\(\text{Property: angle at centre is twice angle on circumference, standing on same arc.}\)

\(\theta= 2 \times 36= 72^{\circ}\)

Circle Geometry, SMB-009

In the diagram, \(OB\) meets the chord \(AC\) such that \(AB = BC\).

The length of chord \(AC = 24\), and \(OC = 13\). 
 

Find the length of \(OB\).  (3 marks)   

Show Answers Only

\(OB=5\)

Show Worked Solution

\(OB \perp AC\ \ \text{(line through centre that bisects chord)}\)

\(BC= \dfrac{1}{2} \times 24 = 12 \)

\(\text{Using Pythagoras in}\ \Delta OBC :\)

\(OB^2\) \(= 13^2-12^2 \)  
  \(= 25\)  
\(\therefore OB\) \(=5\)  

Networks, STD2 N2 2018 FUR1 4 MC

Consider the graph below.
 


 

Which one of the following is not a path for this graph?

  1. `PRQTS`
  2. `PRTSQ`
  3. `PTQSR`
  4. `PTRQS`
Show Answers Only

`C`

Show Worked Solution

`text(By trial and error:)`

`text(Consider option)\ C,`

`PTQSR\ text(is not a path because)\ S\ text(to)\ R`

`text(must go through another vertex.)`

`=> C`

Networks, STD2 N2 2015 FUR1 5 MC

The graph below represents a friendship network. The vertices represent the four people in the friendship network: Kwan (K), Louise (L), Milly (M) and Narelle (N).

An edge represents the presence of a friendship between a pair of these people. For example, the edge connecting K and L shows that Kwan and Louise are friends.

Which one of the following graphs does not contain the same information.
 
 

Show Answers Only

`D`

Show Worked Solution

`text(Option D has Kwan and Milly as friends which is not correct.)`

`=> D`

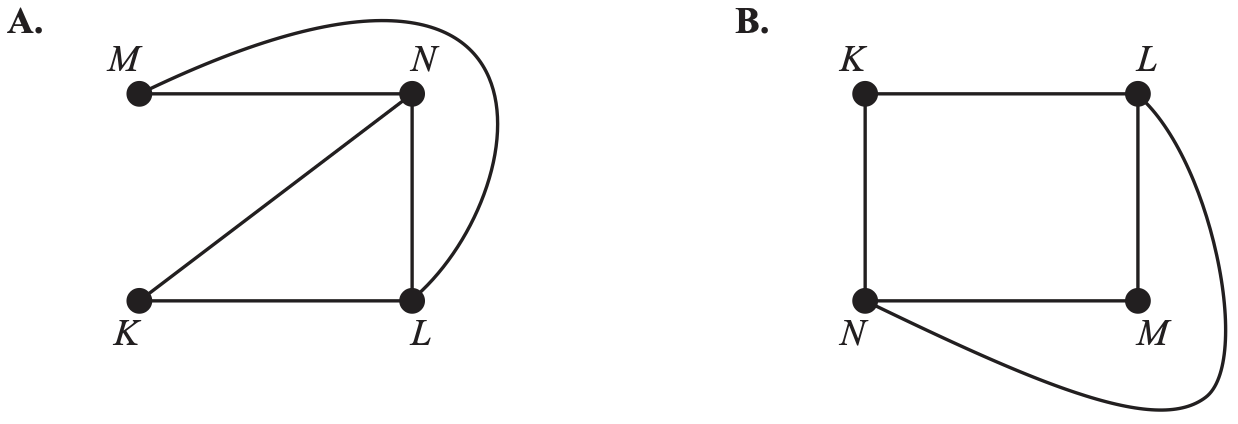
Networks, STD2 N2 2017 FUR1 2 MC

Two graphs, labelled Graph 1 and Graph 2, are shown below.
 

 
The sum of the degrees of the vertices of Graph 1 is

  1. two less than the sum of the degrees of the vertices of Graph 2.
  2. one less than the sum of the degrees of the vertices of Graph 2.
  3. equal to the sum of the degrees of the vertices of Graph 2.
  4. two more than the sum of the degrees of the vertices of Graph 2.
Show Answers Only

`C`

Show Worked Solution

`text(Graph 1)`

`∑\ text(degrees)\ = 3 + 3 + 3 + 3 = 12`

`text(Graph 2)`

`∑\ text(degrees)\ = 2 + 2 + 2 + 2 + 2 + 2 = 12`

`=> C`

Plane Geometry, EXT1 2017 HSC 12a

The points `A`, `B` and `C` lie on a circle with centre `O`, as shown in the diagram. The size of `angleAOC` is 100°.
 

Find the size of `angleABC`, giving reasons.  (2 marks)

Show Answers Only

`130^@`

Show Worked Solution

`text(Reflex)\ angleAOC` `= 360-100`
  `= 260^@`
`:. angleABC` `= 1/2 xx 260^@` `text{(angles at centre and on}`
 `text{circumference of arc}\ AC)`
  `= 130^@`  

Plane Geometry, EXT1 2016 HSC 4 MC

In the diagram, `O` is the centre of the circle `ABC`, `D` is the midpoint of `BC`, `AT` is the tangent at `A` and  `∠ATB = 40^@`.
 

What is the size of the reflex angle `DOA`?

  1. `80^@`
  2. `140^@`
  3. `220^@`
  4. `280^@`
Show Answers Only

`C`

Show Worked Solution

 

`/_ ODT` `=90^@\ \ text{(line through centre bisecting chord)}`
`/_OAT` `= 90^@\ \ text{(tangent ⊥ to radius at point of contact)}`
`/_ DOA` `= 360-(90 + 90 + 40)`
  `= 140^@`

 

`:. DOA\ \ text{(reflex)}` `= 360-140`
  `= 220^@`

`=>   C`

NETWORKS, FUR2 2007 VCAA 1

A new housing estate is being developed.

There are five houses under construction in one location.

These houses are numbered as points 1 to 5 below.
 

NETWORKS, FUR2 2007 VCAA 1

  
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.

  1. What is the minimum number of edges needed to connect the five houses?  (1 mark)

  2. On the diagram above, draw a connected graph with this number of edges.  (1 mark) 

Show Answers Only
  1. `4`
  2.  
    networks-fur2-2007-vcaa-1-answer
Show Worked Solution

a.   `text(Minimum number of edges = 4)`
 

b.   `text(One of many possibilities:)`

networks-fur2-2007-vcaa-1-answer