Expand and simplify
v1 Functions, 2ADV F1 2004 HSC 1c
Solve
EXAMCOPY Algebra, STD2 A4 2014 HSC 29a
The cost of hiring an open space for a music festival is $120 000. The cost will be shared equally by the people attending the festival, so that
- Complete the table below by filling in the THREE missing values. (1 mark)
- Using the values from the table, draw the graph showing the relationship between
and . (2 marks)
- What equation represents the relationship between
and ? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Give ONE limitation of this equation in relation to this context. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Is it possible for the cost per person to be $94? Support your answer with appropriate calculations. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Answers Only
i.
| ii. |  |
iii.
iv.
v.
Show Worked Solution
i.
| ii. | |
♦ Mean mark (iii) 48%
iii.
♦♦♦ Mean mark (iv) 7%
COMMENT: When asked for limitations of an equation, look carefully at potential restrictions with respect to both the domain and range.
COMMENT: When asked for limitations of an equation, look carefully at potential restrictions with respect to both the domain and range.
iv.
v.
♦ Mean mark (v) 38%
EXAMCOPY Algebra, STD2 A4 2022 HSC 24
A student believes that the time it takes for an ice cube to melt (
- Find the equation relating
and . (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- By first completing this table of values, graph the relationship between temperature and time from
to (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
| a. | ||
b.
Show Worked Solution
| a. | ||
♦♦ Mean mark part (a) 29%.
b.
♦ Mean mark 44%.
v2 Functions, 2ADV F1 2017 HSC 1 MC
What is the gradient of the line
EXAMCOPY Functions, 2ADV F1 2009 HSC 1a
Sketch the graph of
--- 8 WORK AREA LINES (style=blank) ---
Show Answers Only
Show Worked Solution
v1 Functions, 2ADV F1 2017 HSC 1 MC
What is the gradient of the line
EXAMCOPY Algebra, STD2 A1 2004 HSC 11 MC
If
Special Properties, SMB-031
In the diagram,
- Show that the size of
is 108°. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- Find the size of
. Give reasons for your answer. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |  |
ii.
Congruency, SMB-016
Special Properties, SMB-020 MC
There are 3 triangles drawn in the lower semi-circle and the angles at the centre are all equal to
The three triangles are best described as:
- isosceles
- scalene
- right-angled
- equilateral
Special Properties, SMB-019
A regular pentagon, a square and an equilateral triangle meet at a point.
What is the size of the angle
--- 7 WORK AREA LINES (style=lined) ---
Special Properties, SMB-018
Special Properties, SMB-017
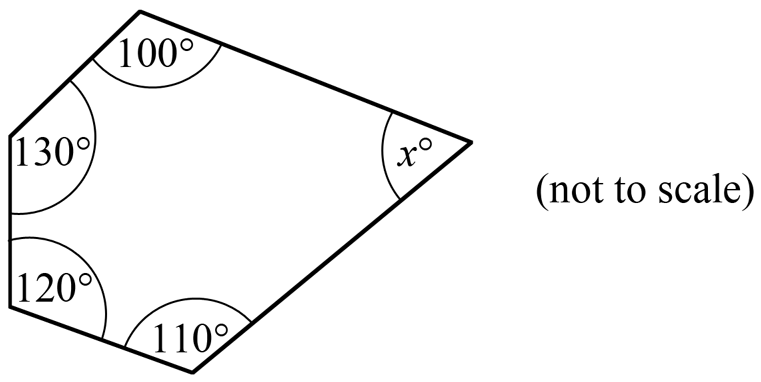
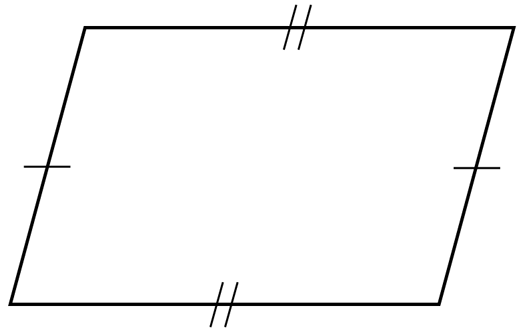
Special Properties, SMB-016
Two identical quadrilaterals fit together to make this regular pentagon.
What is the value of
--- 4 WORK AREA LINES (style=lined) ---
Special Properties, SMB-015
Special Properties, SMB-014
The sum of the interior angles of a 6 sided polygon can be found by first dividing it into triangles from one vertex.
What is the sum of the interior angles of this polygon? (2 marks)
Special Properties, SMB-012
What is the size of
--- 4 WORK AREA LINES (style=lined) ---
Special Properties, SMB-013 MC
Which statement is always true?
- Scalene triangles have two angles that are equal.
- All angles in a parallelogram are equal.
- The opposite sides of a trapezium are equal in length.
- The diagonals of a rhombus are perpendicular to each other.
Special Properties, SMB-011 MC
Special Properties, SMB-010 MC
Which of these are always equal in length?
- the diagonals of a rhombus
- the diagonals of a parallelogram
- the opposite sides of a parallelogram
- the opposite sides of a trapezium
Show Worked Solution
Special Properties, SMB-009 MC
Special Properties, SMB-008
The sum of the internal angles of a polygon can be calculated by drawing triangles from any given vertex as shown below.
What is the size of the angle marked
--- 4 WORK AREA LINES (style=lined) ---
Special Properties, SMB-007 MC
A closed shape has two pairs of equal adjacent sides.
What is the shape?
- rectangle
- trapezium
- kite
- triangle
Special Properties, SMB-006
Eloise makes a sketch of the playground at her school.
What is the size of angle
Congruency, SMB-013
Which two of the triangles below are congruent? (2 marks)
Congruency, SMB-012
Which two of the triangles below are congruent? (2 marks)
Congruency, SMB-015
The two triangles below are congruent.
- Which congruency test would be used to prove the two triangles above are congruent? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Find the values of
and . (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
Special Properties, SMB-005 MC
What is the best description of
- isosceles
- equilateral
- scalene
- right-angled
Congruence, SMB-014
The area of the rectangle in the diagram below is 15 cm2.
Giving reasons, find the area of the trapezium
--- 8 WORK AREA LINES (style=lined) ---
Show Worked Solution
Special Properties, SMB-004 MC
Which one of the following triangles is impossible to draw?
- a right angled triangle with two acute angles
- an isosceles triangle with one right angle
- a scalene triangle with three acute angles
- a right angled triangle with one obtuse angle
Special Properties, SMB-003 MC
Special Properties, SMB-002 MC
A triangle has two acute angles.
What type of angle couldn't the third angle be?
- an acute angle
- an obtuse angle
- a right-angle
- a reflex angle
Special Properties, SMB-001 MC
Which of the following triangle types is impossible to draw?
- a right-angled, scalene triangle
- a right-angled, equilateral triangle
- an obtuse-angled, isosceles triangle
- an acute-angled, scalene triangle
Congruency, SMB-011
The diagram shows a circle with centre
The length of the arc
Prove that
--- 5 WORK AREA LINES (style=lined) ---
Congruency, SMB-010
In the diagram,
- Prove that
. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- Prove that
. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |  |
ii.
Congruency, SMB-008
In the figure below,
Prove that a diagonal of the parallelogram produces two triangles that are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
Congruency, SMB-007
In the figure below,
Prove that this pair of triangles are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Congruency, SMB-006
In the quadrilateral
Prove that this pair of triangles are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Congruency, SMB-005
In the figure below,
Prove that this pair of triangles are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Congruency, SMB-004
In the circle below, centre
Prove that a pair of triangles in this figure are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Congruency, SMB-003
In the figure below, the line
Prove that this pair of triangles are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Congruency, SMB-002
The diagram shows two triangles that touch at the middle of a circle.
Prove that this pair of triangles are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Congruency, SMB-001
The diagram shows two right-angled triangles where
Prove that this pair of triangles are congruent. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-026
The two triangles below are similar.
Find the length of
--- 5 WORK AREA LINES (style=lined) ---
Similarity, SMB-024
Prove that the two triangles in the right cone pictured below are similar. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-023
Show that
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-022
Prove that this pair of triangles are similar. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-021
Prove that this pair of triangles are similar. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-020
Prove that this pair of triangles are similar. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Similarity, SMB-019
Prove that this pair of triangles are similar. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-018
Prove that this pair of triangles are similar. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Similarity, SMB-017
Prove that this pair of triangles are similar. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Congruency, SMB-009
The diagram shows a right-angled triangle
Show that
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
Trigonometry, SMB-067
Find the value of
Trigonometry, SMB-066
Find the value of
--- 5 WORK AREA LINES (style=lined) ---
Trigonometry, SMB-065
Find the value of
--- 5 WORK AREA LINES (style=lined) ---
Trigonometry, SMB-064
Find the value of
Trigonometry, SMB-063
Find the value of
Trigonometry, SMB-062
- 1
- 2
- 3
- …
- 5
- Next Page »