SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Trigonometry, SMB-063

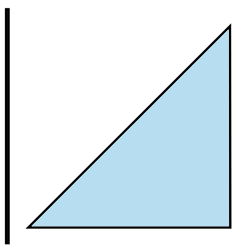
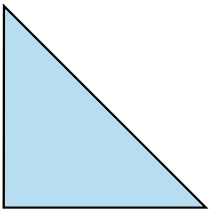
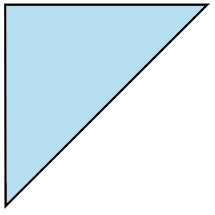
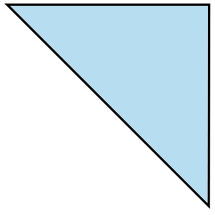
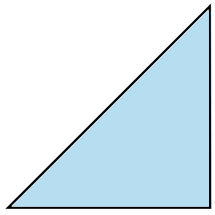
Find the value of \(x\), correct to 1 decimal place.   (3 marks)
 

Show Answers Only

\(x=15.4\ \text{cm}\)

Show Worked Solution
\(a^2\) \(=b^2+c^2-2bc\ \cos A \)  
\(x^2\) \(= 15^2+25^2-2 \times 15 \times 25 \times \cos 35^{\circ}\)  
  \(= 235.63…\)  
\(\therefore x\) \(=15.35…\)  
  \(=15.4\ \text{cm (1 d.p.)} \)  

Trigonometry, SMB-062

Find the value of \(x\), correct to 1 decimal place.   (3 marks)
 

Show Answers Only

\(x=8.8\ \text{m}\)

Show Worked Solution
\(a^2\) \(=b^2+c^2-2bc\ \cos A \)  
\(x^2\) \(= 5^2+9^2-2 \times 5 \times 9 \times \cos 72^{\circ}\)  
  \(= 78.188…\)  
\(\therefore x\) \(=8.842…\)  
  \(=8.8\ \text{m (1 d.p.)} \)  

Trigonometry, SMB-061

Find the value of \(\theta\), correct to the nearest degree.   (3 marks)

Show Answers Only

\(\theta=154^{\circ}\)

Show Worked Solution
\(\dfrac{\sin \theta}{21}\) \(= \dfrac{\sin 12^{\circ}}{10} \)  
\(\sin \theta\) \(= \dfrac{21 \times \sin 12^{\circ}}{10}\)  
\(\theta\) \(=\sin^{-1} (0.4366) \)  
  \(=25.88…^{\circ} \)  
  \(=26^{\circ}\ \text{(nearest degree)} \)  

 
\(\therefore\ \theta = 180-26=154^{\circ}\ \ \text{(angle is obtuse)}\)

Trigonometry, SMB-060

Find the value of \(\alpha\), correct to the nearest degree.   (2 marks)

Show Answers Only

\(\alpha=39^{\circ}\)

Show Worked Solution
\(\dfrac{\sin \alpha}{9}\) \(= \dfrac{\sin 79^{\circ}}{14} \)  
\(\sin \alpha\) \(= \dfrac{9 \times \sin 79^{\circ}}{14}\)  
\(\alpha\) \(=\sin^{-1} (0.6310) \)  
  \(=39.12…^{\circ} \)  
  \(=39^{\circ}\ \text{(nearest degree)} \)  

Trigonometry, SMB-059

Find the value of \(\theta\), correct to the nearest degree.   (2 marks)

Show Answers Only

\(\theta=50^{\circ}\)

Show Worked Solution
\(\dfrac{\sin \theta}{7.5}\) \(= \dfrac{\sin 66^{\circ}}{8.9} \)  
\(\sin \theta\) \(= \dfrac{7.5 \times \sin 66^{\circ}}{8.9}\)  
\(\theta\) \(=\sin^{-1} (0.7698) \)  
  \(=50.33…^{\circ} \)  
  \(=50^{\circ}\ \text{(nearest degree)} \)  

Trigonometry, SMB-058

Find the value of \(\theta\), correct to the nearest degree.   (2 marks)

Show Answers Only

\(\theta=53^{\circ}\)

Show Worked Solution
\(\dfrac{\sin \theta}{6}\) \(= \dfrac{\sin 37^{\circ}}{4.5} \)  
\(\sin \theta\) \(= \dfrac{6 \times \sin 37^{\circ}}{4.5}\)  
\(\theta\) \(=\sin^{-1} (0.8024) \)  
  \(=53.361…^{\circ} \)  
  \(=53^{\circ}\ \text{(nearest degree)} \)  

Trigonometry, SMB-057

Find \(\alpha\), to the nearest degree, such that

\(\dfrac{\sin \alpha}{8} = \dfrac{\sin 60^{\circ}}{11} \)   (2 marks)

Show Answers Only

\(\alpha=39^{\circ}\)

Show Worked Solution
\(\dfrac{\sin \alpha}{8}\) \(= \dfrac{\sin 60^{\circ}}{11} \)  
\(\sin \alpha\) \(= \dfrac{8 \times \sin 60^{\circ}}{11}\)  
\(\alpha\) \(=\sin^{-1} (0.6298) \)  
  \(=39^{\circ}\ \text{(nearest degree)} \)  

Trigonometry, SMB-056

Find \(\theta\), to the nearest degree, such that

\(\dfrac{12}{\sin \theta} = \dfrac{15}{\sin 26^{\circ}} \)   (2 marks)

Show Answers Only

\(\theta=21^{\circ}\)

Show Worked Solution
\(\dfrac{12}{\sin \theta}\) \(= \dfrac{15}{\sin 26^{\circ}} \)  
\(\dfrac{\sin \theta}{12}\) \(= \dfrac{\sin 26^{\circ}}{15} \)  
\(\sin \theta\) \(= \dfrac{12 \times \sin 26^{\circ}}{15}\)  
\(\theta\) \(=\sin^{-1} (0.3507) \)  
  \(=21^{\circ}\ \text{(nearest degree)} \)  

Trigonometry, SMB-055

Find the value of \(x\), correct to 1 decimal place.   (2 marks)
 

Show Answers Only

\(x=9.9\ \text{cm}\)

Show Worked Solution

\(\text{Angle needed}\ = 180-(115+34) = 31^{\circ}\)

\(\dfrac{x}{\sin31^{\circ}}\) \(=\dfrac{17.5}{\sin 115^{\circ}}\)  
\(x\) \(=\dfrac{17.5 \times \sin 31^{\circ}}{\sin 115^{\circ}}\)  
  \(=9.94…\)  
  \(=9.9\ \text{cm (to 1 d.p.)}\)  

Trigonometry, SMB-054

Find the value of \(x\), correct to 1 decimal place.   (2 marks)

Show Answers Only

\(x=7.2\ \text{cm}\)

Show Worked Solution

\(\text{Angle needed}\ = 180-(81+43) = 56^{\circ}\)

\(\dfrac{x}{\sin56^{\circ}}\) \(=\dfrac{8.6}{\sin 81^{\circ}}\)  
\(x\) \(=\dfrac{8.6 \times \sin 56^{\circ}}{\sin 81^{\circ}}\)  
  \(=7.218…\)  
  \(=7.2\ \text{cm (to 1 d.p.)}\)  

Trigonometry, SMB-053

Find the value of \(x\), correct to 1 decimal place.  (2 marks)

Show Answers Only

\(x=8.0\ \text{cm}\)

Show Worked Solution
\(\dfrac{x}{\sin42^{\circ}}\) \(=\dfrac{12}{\sin 86^{\circ}}\)  
\(x\) \(=\dfrac{12 \times \sin 42^{\circ}}{\sin 86^{\circ}}\)  
  \(=8.049…\)  
  \(=8.0\ \text{cm (to 1 d.p.)}\)  

Trigonometry, SMB-052

Find the value of \(x\), correct to 1 decimal place.  (2 marks)

Show Answers Only

\(x=13.9\ \text{m}\)

Show Worked Solution
\(\dfrac{x}{\sin43^{\circ}}\) \(=\dfrac{20}{\sin 78^{\circ}}\)  
\(x\) \(=\dfrac{20 \times \sin 43^{\circ}}{\sin 78^{\circ}}\)  
  \(=13.944…\)  
  \(=13.9\ \text{cm (to 1 d.p.)}\)  

Trigonometry, SMC-051

Solve for \(b\), giving your answer correct to 1 decimal place.

\(\dfrac{b}{\sin 22^{\circ}} =  \dfrac{17}{\sin 67^{\circ}}\)  (2 marks)

Show Answers Only

\(b=6.9\)

Show Worked Solution
\(\dfrac{b}{\sin 22^{\circ}}\) \(= \dfrac{17}{\sin 67^{\circ}}\) 
\(b\) \(=\dfrac{17 \times \sin 22^{\circ}}{\sin 67^{\circ}}\)
  \(=6.9\ \text{(to 1 d.p.)}\)

Trigonometry, SMB-050

Solve for \(a\), giving your answer correct to 1 decimal place.

\(\dfrac{6}{\sin 53^{\circ}} =  \dfrac{a}{\sin 27^{\circ}}\)  (2 marks)

Show Answers Only

\(a=3.4\)

Show Worked Solution
\(\dfrac{6}{\sin 53^{\circ}}\) \(= \dfrac{a}{\sin 27^{\circ}}\) 
\(a\) \(=\dfrac{6 \times \sin 27^{\circ}}{\sin 53^{\circ}}\)
  \(=3.4\ \text{(to 1 d.p.)}\)

Measurement, STD2 M6 2023 HSC 35

The diagram shows triangle `ABC`.
 

Calculate the area of the triangle, to the nearest square metre.  (3 marks)

Show Answers Only

`147\ text{m}^2`

Show Worked Solution

`text{Using the sine rule:}`

`(CB)/sin60^@` `=12/sin25^@`  
`CB` `=sin60^@ xx 12/sin25^@`  
  `=24.590…`  

 
`angleACB=180-(60+25)=95^@\ \ text{(180° in Δ)}`
 

`text{Using the sine rule (Area):}`

`A` `=1/2 xx AC xx CB xx sin angleACB`  
  `=1/2 xx 12 xx 24.59 xx sin95^@`  
  `=146.98…`  
  `=147\ text{m}^2`  

Circles and Hyperbolas, SMB-019

Find the centre and radius of the circle with the equation

     `x^2+6x+y^2-y+3=0`  (2 marks)

Show Answers Only

`text{Centre}\ (-3,1/2),\ text{Radius}\ = 5/2`     

Show Worked Solution
`x^2+6x+y^2-y+3` `=0`  
`x^2+6x+9+y^2-y+1/4-25/4` `=0`  
`(x+3)^2+(y-1/2)^2` `=25/4`  
`(x+3)^2+(y-1/2)^2` `=(5/2)^2`  

 
`text{Centre}\ (-3,1/2),\ text{Radius}\ = 5/2`     

Circles and Parabolas, SMB-018

  1. Find the centre and radius of the circle with the equation
  2.      `x^2-2x+y^2+3y-3/4=0`  (2 marks)

  3. Sketch the circle on the graph below.  (1 mark)
     

Show Answers Only

a.   `text{Centre}\ (1,-3/2),\ \ text{Radius}\ =2`

b.  


        

Show Worked Solution
a.    `x^2-2x+y^2+3y-3/4` `=0`
  `x^2-2x+1+y^2+3y+9/4-4` `=0`
  `(x-1)^2+(y+3/2)^2` `=2^2`

 
`text{Centre}\ (1,-3/2),\ \ text{Radius}\ =2`

b.   

 

Circles and Hyperbolas, SMB-017

  1. Find the centre and radius of the circle with the equation
  2.      `x^2-4x+y^2+6y+9=0`  (2 marks)

  3. Sketch the circle on the graph below.  (1 mark)

Show Answers Only

a.   `text{Centre}\ (2,-3),\ text{Radius}\ = 2`

b.   


        

Show Worked Solution
a.    `x^2-4x+y^2+6y+9` `=0`
  `x^2-4x+4+y^2+6y+9-4` `=0`
  `(x-2)^2+(y+3)^2` `=2^2`

  
`:.\ text{Centre}\ (2,-3),\ text{Radius}\ = 2`

b.   

Circles and Hyperbolas, SMB-014

  1. Find the centre and radius of the circle with the equation
  2.      `x^2+6x+y^2+4y+4=0`  (2 marks)

  3. Sketch the circle on the graph below.  (1 mark)
     

Show Answers Only

a.   `(x+3)^2 + (y+2)^2 = 3^2`

`:.\ text(Centre:)\ (-3,-2)\text(, Radius:)\ 3`

b.   

Show Worked Solution
a.    `x^2+6x+y^2+4y+4` `=0`
  `x^2+6x+9+y^2+4y+4-9` `=0`
  `(x+3)^2+(y+2)^2` `=3^2`

  
`:.\ text(Centre:)\ (-3,-2)\text(, Radius:)\ 3`

  
b.   

Circles and Hyperbolas, SMB-013

  1. Write down the equation of the circle with centre `(1, -2)` and radius 2.  (1 mark)

  2. On the graph, sketch the circle in part (a).  (2 marks)

Show Answers Only

a.   `(x-1)^2 + (y+2)^2 = 4`

b.    
     

Show Worked Solution

a.   `text{Circle with centre}\ (1,-2),\ r = 2:`

`(x-1)^2 + (y+2)^2 = 4`
 

b.   

Circles and Hyperbolas, SMB-010 MC

A circle with centre `(a,-2)` and radius 5 units has equation

`x^2-6x + y^2 + 4y = b`  where  `a`  and  `b`  are real constants.

The values of  `a`  and  `b`  are respectively

  1. −3 and 38
  2. 3 and 12
  3. −3 and −8
  4. 3 and 18
Show Answers Only

`B`

Show Worked Solution

`x^2-6x + y^2 + 4y=b`

`text(Completing the squares:)`

`x^2-6x + 3^2-9 + y^2 + 4y + 2^2-4` `= b`
`(x-3)^2 + (y + 2)^2-13` `= b`
`(x-3)^2 + (y + 2)^2` `= b + 13`

 
`:. a=3`

`:. b+13=25\ \ =>\ \ b=12`

`=> B`

Quadratics, SMB-015

The diagram shows the curve with equation  `y = x^2-7x + 10`. The curve intersects the `x`-axis at points `A and B`. The point `C` on the curve has the same `y`-coordinate as the `y`-intercept of the curve.
 

 

  1. Find the `x`-coordinates of points `A and B.`  (2 marks)

  2. Write down the coordinates of `C.`  (2 marks)

Show Answers Only
  1. `A = 2,\ \ B = 5`
  2. `(7, 10)`
Show Worked Solution
i.    `y` `= x^2-7x + 10`
  `= (x-2) (x-5)`

 
`:.x = 2 or 5`

`:.\ \ x text(-coordinate of)\ \ A = 2`

`x text(-coordinate of)\ \ B = 5`

 

ii.    `y\ text(intercept occurs when)\ \ x = 0`

`=>y text(-intercept) = 10`
 

`C\ text(occurs at intercept:)`

`y` `= x^2-7x + 10` `\ \ \ \ \ text{…  (1)}`
`y` `= 10` `\ \ \ \ \ text{…  (2)}`

 
`(1) = (2)`

`x^2-7x + 10` `= 10`
`x^2-7x` `= 10`
`x (x-7)` `= 10`

 
`x = 0 or 7`

`:.\ C\ \ text(is)\ \ (7, 10)`

Quadratics, SMB-014

The parabola  `y = −2x^2 + 8x`  and the line  `y = 2x`  intersect at the origin and at the point  `A`.
 

Find the  `x`-coordinate of the point `A`.    (2 marks)

Show Answers Only

`x=3`

Show Worked Solution
i.  

`x\text(-coordinate of)\ A:`

`y` `= 2x\ \ \ \ \ …\ text{(i)}`
`y` `= -2x^2 + 8x\ \ \ \ \ …\ text{(ii)}`

 
`text(Subst)\ y = 2x\ text{from (i) into (ii):}`

`-2x^2 + 8x` `= 2x`
`-2x^2 + 6x` `= 0`
`-2x (x-3)` `= 0`

  
`:.\ x = 0\ text(or)\ 3`

`:.\ x\text(-coordinate of)\ A\ text(is 3)`

Circles and Hyperbolas, SMB-009

Sketch the graph of  `y=4/(x-3)`.  (3 marks)

Show Answers Only

Show Worked Solution

`text{Vertical asymptote at}\ \ x=3`

`text{As}\ \ x->oo, \ y->0`

`text{Horizontal asymptote at}\ \ y=0`

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -1 & \ \ 0\ \  & \ \ 2\ \  & \ \ 4\ \  & \ \ 5\ \  \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & -1 & -\frac{4}{3} & -4 & 4 & 2\\
\hline
\end{array}

 

Circles and Hyperbolas, SMB-008

Sketch the graph of  `y=2/(3-x)`.  (3 marks)
 

Show Answers Only

Show Worked Solution

`text{Vertical asymptote at}\ \ x=3`

`text{As}\ \ x->oo, \ y->0`

`text{Horizontal asymptote at}\ \ y=0`

\begin{array} {|l|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -1 & \ \ 0\ \  & \ \ 2\ \  & \ \ 4\ \  & \ \ 5\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & \frac{1}{2} & \frac{2}{3} & 2 & -2 & -1\\
\hline
\end{array}

 

Circles and Hyperbolas, SMB-007

Sketch the graph of  `y=3/(x+1)`.  (2 marks)
 

Show Answers Only

Show Worked Solution

`text{Vertical asymptote at}\ \ x=-1`

`text{As}\ \ x->oo, \ y->0`

`text{Horizontal asymptote at}\ \ y=0`

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -3  & -2  & -1  & \ \ 0\ \  & \ \ 1\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & -\frac{3}{2} & -3 & ∞ & 3 & \frac{3}{2} \\
\hline
\end{array}

Circles and Hyperbolas, SMB-006

Sketch the graph of  `y=1/(x-2)`.  (2 marks)

Show Answers Only

Show Worked Solution

`text{Vertical asymptote at}\ \ x=2`

`text{As}\ \ x->oo, \ y->0`

`text{Horizontal asymptote at}\ \ y=0`

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \  & \ \ 3\ \  & \ \ 4\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & -\frac{1}{2} & -1 & ∞ & 1 & \frac{1}{2} \\
\hline
\end{array}

Circles and Hyperbolas, SMB-004

  1. List all asymptotes of the graph  `y=2-1/x`.  (2 marks)

  2. Hence, sketch the graph of  `y=2-1/x`.  (2 marks)

Show Answers Only

i.    `text{Vertical asymptote at}\ \ x=0`

`text{Horizontal asymptote at}\ \ y=2`

ii.

Show Worked Solution

i.     `y=2-1/x`

`text{Vertical asymptote at}\ \ x=0`

`text{As}\ x->oo, \ 1/x -> 0\ \ => 2-1/x -> 2`

`text{Horizontal asymptote at}\ \ y=2`

ii.  

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -2 & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & \frac{5}{2} & 3 & ∞ & 1 & \frac{3}{2} \\
\hline
\end{array}

Circles and Hyperbolas, SMB-003

Sketch the graph of  `y=2/x+2`.

Clearly mark all asymptotes.  (3 marks)

Show Answers Only

Show Worked Solution

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -2 & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & 1 & 0 & ∞ & 4 & 3 \\
\hline
\end{array}

Circles and Hyperbola, SMB-002

Sketch the graph of  `y=-2/x`.  (2 marks)

Show Answers Only

Show Worked Solution

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -2 & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & 1 & 2 & ∞ & -2 & -1 \\
\hline
\end{array}

Circles and Hyperbola, SMB-001

Sketch the graph of  `y=3/x`.  (2 marks)

Show Answers Only

Show Worked Solution

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\ \ x\ \ \rule[-1ex]{0pt}{0pt} & -2 & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \ \\
\hline
\rule{0pt}{2.5ex}\ \ \ y\ \ \rule[-1ex]{0pt}{0pt} & -\frac{3}{2} & -3 & ∞ & 3 & \frac{3}{2} \\
\hline
\end{array}

Quadratics, SMB-013

Factorise the parabola described by the equation  `y=-x^2-x+12`  and find its vertex.  (3 marks)

Show Answers Only

`y=(3-x)(x+4)`

`text{Vertex}\ = (-1/2,12 1/4)`

Show Worked Solution
`y` `=-x^2-x+12`  
  `=-(x^2+x-12)`  
  `=-(x+4)(x-3)`  
  `=(3-x)(x+4)`  

 

`text{Solutions at}\ \ x=3, -4`

 `text{Line of symmetry at mid-point of solutions.}`

  `x=(3+(-4))/2=-1/2`
 

`text{Substitute}\ \ x=-1/2\ \ text{into}\ \ y=-x^2-x+12`

`y=-1/4+1/2+12=12 1/4`

`:.\ text{Vertex}\ = (-1/2,12 1/4)`

Quadratics, SMB-012

  1. Factorise  `y=x^2-8x+15`  (1 mark)

  2. Find the vertex of the parabola with equation  `y=x^2-8x+15`  (2 marks)

Show Answers Only
  1. `y=(x-5)(x-3)`
  2. `text{Vertex}\ = (4,-1)`
Show Worked Solution
i.   `y` `=x^2-8x+15`  
  `=(x-5)(x-3)`  

 

ii.    `text{Solutions at}\ \ x=3,5.`

 `text{Line of symmetry at mid-point of solutions.}`

  `x=(3+5)/2=4`
 

`text{Substitute}\ \ x=4\ \ text{into}\ \ y=x^2-8x+15`

`y=4^2-8xx4+15=-1`

`:.\ text{Vertex}\ = (4,-1)`

Quadratics, SMB-011

  1. Factorise  `y=2x^2+5x-3`  (1 mark)

  2. Find the vertex of the parabola with equation  `y=2x^2+5x-3`  (2 marks)

Show Answers Only
  1. `y=(2x-1)(x+3)`
  2. `text{Vertex}\ = (-5/4,-49/8)`
Show Worked Solution
i.   `y` `=2x^2+5x-3`  
  `=(2x-1)(x+3)`  

 

ii.    `text{Solutions at}\ \ x=1/2,-3.`

 `text{Line of symmetry at mid-point of solutions.}`

  `x=(1/2+(-3))/2=-5/4`
 

`text{Substitute}\ \ x=-5/4\ \ text{into}\ \ y=2x^2+5x-3`

`y=2xx(-5/4)^2-5xx5/4-3=-49/8`

`:.\ text{Vertex}\ = (-5/4,-49/8)`

Quadratics, SMB-010

  1. Factorise  `y=6-x-x^2`  (2 marks)

  2. Find the vertex of the parabola with equation  `y=6-x-x^2`  (2 marks)

Show Answers Only
  1. `y=(2-x)(x+3)`
  2. `text{Vertex}\ = (-1/2,6 1/4)`
Show Worked Solution
i.   `y` `=6-x-x^2`  
  `=-(x^2+x-6)`  
  `=-(x-2)(x+2)`  
  `=(2-x)(x+3)`  

 

ii.    `text{Solutions at}\ \ x=2,-3.`

 `text{Line of symmetry at mid-point of solutions.}`

  `x=(2+(-3))/2=-1/2`
 

`text{Substitute}\ \ x=-1/2\ \ text{into}\ \ y=6-x-x^2`

`y=6+1/2-1/4=6 1/4`

`:.\ text{Vertex}\ = (-1/2,6 1/4)`

Quadratics, SMB-009

By completing the square, find the coordinates of the vertex of the parabola with equation

  `y=x^2-3x+1`  (3 marks)

Show Answers Only

`(3/2,-5/4)`

Show Worked Solution
`y` `=x^2-3x+1`  
  `=x^2-3x+9/4-5/4`  
  `=(x-3/2)^2-5/4`  

 
`:.\ text{Vertex}\ = (3/2,-5/4)`

Quadratics, SMB-008

By completing the square, find the coordinates of the vertex of the parabola with equation

  `y=x^2+8x+9`  (3 marks)

Show Answers Only

`(-4,-7)`

Show Worked Solution
`y` `=x^2+8x+9`  
  `=x^2+8x+16-7`  
  `=(x+4)^2-7`  

 
`:.\ text{Vertex}\ = (-4,-7)`

Quadratics, SMB-007

By completing the square, find the coordinates of the vertex of the parabola with equation

  `y=x^2-6x-4`  (3 marks)

Show Answers Only

`(3,-13)`

Show Worked Solution
`y` `=x^2-6x-4`  
  `=x^2-6x+9-13`  
  `=(x-3)^2-13`  

 
`:.\ text{Vertex}\ = (3,-13)`

Exponentials, SMB-004

Sketch the graph of  `y=3(2^(-x))-1`  (3 marks)

Show Answers Only

Show Worked Solution

\begin{array} {|l|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} x \rule[-1ex]{0pt}{0pt} & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \  & \ \ 3\ \  \\
\hline
\rule{0pt}{2.5ex} y \rule[-1ex]{0pt}{0pt} & 5 & 2 & \frac{1}{2} & -\frac{1}{4} & -\frac{5}{8}\\
\hline
\end{array}

Exponential, SMB-003

By completing the table of values, sketch the graph of  `y=2^(-x)`  (3 marks)

\begin{array} {|l|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ x\ \  \rule[-1ex]{0pt}{0pt} & -2 & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \  \\
\hline
\rule{0pt}{2.5ex} \ \ y\ \  \rule[-1ex]{0pt}{0pt} &  &  & 1 &  & \\
\hline
\end{array}

Show Answers Only

Show Worked Solution

\begin{array} {|l|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} x \rule[-1ex]{0pt}{0pt} & -2 & -1 & \ \ 0\ \  & \ \ 1\ \  & \ \ 2\ \  \\
\hline
\rule{0pt}{2.5ex} y \rule[-1ex]{0pt}{0pt} & 4 & 2 & 1 & \frac{1}{2} & \frac{1}{4}\\
\hline
\end{array}

Transformations, SMB-024

Points `P` and `Q`, shown on the Cartesian plane diagram, are rotated 180° about the origin and become points `P^(′)` and `Q^(′)`.

 

Plot the points `P^(′)` and `Q^(′)` on the diagram.  (3 marks)

Show Answers Only

`P^(′)(2,1)`

`Q^(′)(-4,2)`

Show Worked Solution

`text{Rotating 180° = Rotating 90° twice (in either direction)}`

`text{1st 90° rotation (clockwise):}`

`P(-2,-1)\ ->\ (-1,2)`

`Q(4,-2)\ ->\ (-2,-4)`
 

`text{2nd 90° rotation (clockwise):}`

`(-1,2)\ ->\ P^(′)(2,1)`

`(-2,-4) \ ->\ Q^(′)(-4,2)`

 

Transformations, SMB-023

Point `Q(3,1)` on the Cartesian plane is rotated 180° about the origin in a clockwise direction to become point `Q^(′)`.

What are the coordinates of `Q^(′)`.  (2 marks)

Show Answers Only

`Q^(′)(-3,-1)`

Show Worked Solution

`text{Rotating 180° = Rotating 90° twice (in either direction)}`

`text{1st 90° rotation (clockwise):}`

`Q(3,1)\ ->\ (1,-3)`

`text{2nd 90° rotation (clockwise):}`

`(1,-3)\ ->\ Q^(′)(-3,-1)`

Transformations, SMB-022

Point `A(4,-3)` on the Cartesian plane is rotated 90° about the origin in a clockwise direction to become point `A^(′)`.

What are the coordinates of `A^(′)`.  (1 mark)

Show Answers Only

`A^(′)(-3,-4)`

Show Worked Solution

`A^(′)(-3,-4)`

Transformations, SMB-021

Point `P(-3,-7)` on the Cartesian plane is rotated 90° about the origin in an anticlockwise direction to become point `P^(′)`.

What are the coordinates of `P^(′)`.  (1 mark)

Show Answers Only

`P^(′)(7,-3)`

Show Worked Solution

`P^(′)(7,-3)`

Transformations, SMB-020

Points `P` and `Q`, shown on the Cartesian plane diagram, are rotated 90° about the origin in a clockwise direction to become points `P^(′)` and `Q^(′)`.

Plot the points `P^(′)` and `Q^(′)` on the diagram.  (2 marks)

Show Answers Only

Show Worked Solution

Transformations, SMB-019

Points `A` and `B`, shown on the Cartesian plane diagram, are rotated 90° about the origin in an anticlockwise direction to become points `A^(′)` and `B^(′)`.

Plot the points `A^(′)` and `B^(′)` on the diagram.  (2 marks)

Show Answers Only

Show Worked Solution

Transformations, SMB-015

Gabby put 5 points on a grid and labelled them `A` to `E`, as shown on the diagram below.

Point `A` is 35 millimetres from point `D.`

Gabby adds a sixth point, `F` so that the arrangement of points has one line of symmetry.

How far is point `F` from point `B?`  (3 marks)

Show Answers Only

`42\ text{mm}`

Show Worked Solution

`A\ text(to)\ D\ text(is 35 mm)`

`=> 1\ text(grid is 7 mm × 7 mm)`
 

`text(Point)\ F\ text(is added below:)`

`:.\ text(Distance)\ B\ text(to)\ F`

`= 6 xx 7`

`= 42\ text(mm)`

Transformations, SMB-013

The trapezium `ABCD` is moved to the new position shown by trapezium `SRQP.`

Which of these transformations resulted in the new position?

  1. Rotate `ABCD` 180° clockwise about the origin.
  2. Rotate `ABCD` 270° clockwise about the origin.
  3. Reflect `ABCD` across the `x`-axis, then translate 8 units left.
  4. Reflect `ABCD` across the `y`-axis, then translate 7 units down.
Show Answers Only

`C`

Show Worked Solution

`text(Reflection in the)\ xtext(-axis:)`

`ABCD -> A^{prime}B^{prime}C^{prime}D^{prime}`

`text(Translate 8 units left:)`

`A^{prime}B^{prime}C^{prime}D^{prime} -> SRQP`

`=>C`

Transformations, SMB-012 MC

Rochelle drew a pattern which is pictured below.

Rochelle rotates the pattern.

How much does Rochelle to turn the pattern until it looks exactly the same?

  1. `1/8\ text(turn)`
  2. `1/4\ text(turn)`
  3. `1/2\ text(turn)`
  4. `text(1 turn)`
Show Answers Only

`B`

Show Worked Solution

`text(Outer pattern looks the same every)\ \ 1/8\ \ text(turn).`

`text(Inner cross pattern looks the same every)\ \ 1/4\ \ text(turn).`

`:.\ text(Whole pattern looks the same every)\ \ 1/4\ \ text(turn).`

`=>B`

Transformations, SMB-010

This shape will be translated 4 units to the right and 2 units up.

Where will the image of the point `A` be located after the shape is translated?  (2 marks)

Show Answers Only

`(1,−3)`

Show Worked Solution

`text(Current position)\ A(−3,−5)`

`text(Translate 4 units to right:)`

`A(−3 + 4,−5) \ -> \ (1,−5)`
 

`text(Translate 2 units up:)`

`(1,−5+2 ) \ -> \ (1,−3)`
 

`:. text(Image of)\ A\ text(is)\ (1,−3)`