SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Financial Maths, 2ADV M1 2024 HSC 24

Jack intends to deposit $80 into a savings account on the first day of each month for 24 months. The interest rate during this time is 6% per annum, compounded monthly.

  1. Calculate how much money Jack will have in his account at the end of the 24 months.   (3 marks)
  2. A table of future value interest factors could have been used to calculate how much money Jack would have in his account at the end of the 24 months.
  3. Part of the table is shown.
     

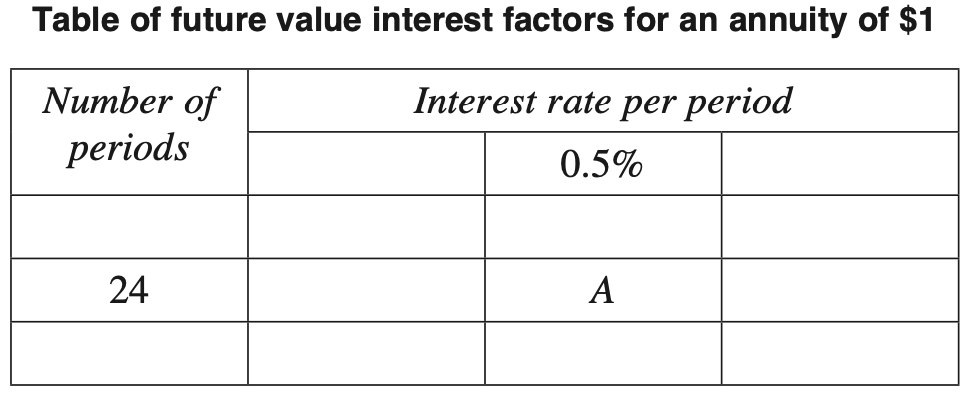
  1. What is the value of \(A\) in the table? Give your answer correct to 3 decimal places.   (1 mark)
Show Answers Only

a.   \(A_{24}=\$2044.73\)

b.   \(A=25.559\)

Show Worked Solution

a.   \(r=\dfrac{6\%}{12}=0.5\%\ \text{per month}\)

\(\text{Let}\ \ A_n=\ \text{Amount after}\ n\ \text{months}\)

\(A_1\) \(=80(1.005)\)  
\(A_2\) \(=[80(1.005)+80](1.005)\)  
  \(=80(1.005)^2+80(1.005) \)  
\(\vdots\)    
\(A_n\) \(=80(1.005)^n+80(1.005)^{n-1}+ … + 80(1.005) \)  
  \(=80\underbrace{(1.005+1.005^2+ … + 1.005^n)}_{\text{GP where}\ \ a=1.005, r=1.005} \)  
  \(=80\Bigg(\dfrac{1.005(1.005^{n}-1)}{1.005-1}\Bigg) \)  

 
\(\text{After 24 months:}\)

\(A_{24}\) \(=80\Bigg(\dfrac{1.005(1.005^{24}-1)}{1.005-1}\Bigg) \)  
  \(=$2044.73 \ \text{(nearest cent)}\)  

  

b.    \(FV\) \(= 80 \times A\)
  \(2044.73\) \(=80 \times A\)
  \(A\) \(=\dfrac{2044.73}{80}\)
    \(=25.5591…\)
    \(=25.559\ \text{(3 d.p.)}\)

Financial Maths, 2ADV M1 2021 HSC 29

  1. On the day that Megan was born, her grandfather deposited $5000 into an account earning 3% per annum compounded annually. On each birthday after this, her grandfather deposited $1000 into the same account, making his final deposit on Megan’s 17th birthday. That is, a total of 18 deposits were made.
  2. Let `A_n` be the amount in the account on Megan’s `n`th birthday, after the deposit is made.
  3. Show that  `A_3 = $8554.54`.  (2 marks)

  4. On her 17th birthday, just after the final deposit is made, Megan has $30 025.83 in her account. You are NOT required to show this.
  5. Megan then decides to leave all the money in the same account continuing to earn interest at 3% per annum compounded annually. On her 18th birthday, and on each birthday after this, Megan withdraws $2000 from the account.
  6. How many withdrawals of $2000 will Megan be able to make?  (3 marks)

Show Answers Only
  1. `text(See Worked Solution)`
  2. `20`
Show Worked Solution

a.   `A_1 = 5000(1.03) + 1000`

`A_2` `= [5000(1.03) + 1000](1.03) + 1000`
  `= 5000(1.03)^2 + 1000(1.03) + 1000`
`A_3` `= 5000(1.03)^3 + 1000(1.03)^2 + 1000(1.03) + 1000`
  `= 8554.535`
  `= $8554.54`

 

b.   `text(Megan’s 18th birthday onwards:)`

`A_1 = 30\ 025.83(1.03) – 2000`

`A_2` `= [30\ 025.83(1.03) – 2000](1.03) – 2000`
  `= 30\ 025.83(1.03)^2 – 2000(1.03) – 2000`
  `vdots`
`A_n` `= 30\ 025.83(1.03)^n – 2000(1 + 1.03 + 1.03^2 + … + 1.03^(n – 1))`

 

`text(Find)\ n\ text(when)\ \ A_n = 0:`

`30\ 025.83(1.03)^n` `= 2000[(a(r^n – 1))/(r – 1)]`
  `= 2000((1.03^n – 1)/(1.03 – 1))`
`30\ 025.83(1.03)^n` `= 66\ 666.67(1.03)^n – 66\ 666.67`
`36\ 640.84(1.03)^n` `= 66\ 666.67`
`1.03^n` `= (66\ 666.67)/(36\ 640.84)`
`n ln 1.03` `= ln ((66\ 666.67)/(36\ 640.84))`
`n` `= (ln ((66\ 666.67)/(36\ 640.84)))/(ln 1.03)`
  `= 20.24…`

 
`:.\ text(Megan can make 20 withdrawals of $2000.)`

Financial Maths, 2ADV M1 2004 HSC 7c

Betty decides to set up a trust fund for her grandson, Luis. She invests $80 at the beginning of each month. The money is invested at 6% per annum, compounded monthly.

The trust fund matures at the end of the month of her final investment, 25 years after her first investment. This means that Betty makes 300 monthly investments.

  1. After 25 years, what will be the value of the first $80 invested?  (2 marks)

  2. By writing a geometric series for the value of all Betty’s investments, calculate the final value of Luis’ trust fund.  (3 marks)

Show Answers Only
  1. `$357.20\ \ text(to the nearest cent)`
  2. `$55\ 716.71\ \ text(to the nearest cent)`
Show Worked Solution

i.    `A = P(1 + r/(100))^n`

`P` `= $80`
`n` `= 300\ \ text(months)`
`r` `=\ text(6%  per annum)`
  `=\ text(0.5%  per month)`
`:.A`

`= 80(1 + (0.5)/(100))^300`
  `= 80(1.005)^300`
  `= 357.1975…`
  `= $357.20\ \ text{(nearest cent)}`

 

ii.   `A_1` `= 80(1.005)^300`
  `A_2` `= 80(1.005)^299`
  `A_3` `= 80(1.005)^298`
    ` vdots`
  `A_300` `= 80(1.005)^1`

 

`:.\ text(Final value of  fund)`

`= 80(1.005)^300 + 80(1.005)^299 + … + 80(1.005)^1`

`= 80[1.005^300 + 1.005^299 + … + 1.005^1]`

`= 80[1.005^1 + 1.005^2 + … + 1.005^300]`

`=>\ text(GP where)\ \ \ a = 1.005, \ r = 1.005, \ n = 300`

`= 80[(a(r^n − 1))/(r − 1)]`

`= 80[(1.005(1.005^300 − 1))/(1.005 − 1)]`

`= 55\ 716.714…`

`= $55\ 716.71\ \ text(to the nearest cent.)`

Financial Maths, 2ADV M1 2007 HSC 9c

Mr and Mrs Caine each decide to invest some money each year to help pay for their son’s university education. The parents choose different investment strategies.

Mr Caine makes 18 yearly contributions of $1000 into an investment fund. He makes his first contribution on the day his son is born, and his final contribution on his son’s seventeenth birthday. His investment earns 6% compound interest per annum.

  1. Find the total value of Mr Caine’s investment on his son’s eighteenth birthday.  (3 marks)

Mrs Caine makes her contributions into another fund. She contributes $1000 on the day of her son’s birth, and increases her annual contribution by 6% each year. Her investment also earns 6% compound interest per annum.

  1. Find the total value of Mrs Caine’s investment on her son’s third birthday (just before she makes her fourth contribution).  (2 marks)

  2. Mrs Caine also makes her final contribution on her son’s seventeenth birthday. Find the total value of Mrs Caine’s investment on her son’s eighteenth birthday.  (1 mark)

Show Answers Only
  1. `$32\ 760\ \ \ text{(nearest dollar)}`
  2. `$3573\ \ \ text{(nearest dollar)}`
  3. `$51\ 378\ \ \ text{(nearest dollar)}`
Show Worked Solution

i.  `text(Let)\ A_n = text(value of the investment after)\ n\ text(years)`

`A_1` `= 1000 (1.06)`
`A_2` `= A_1 (1.06) + 1000 (1.06)`
  `= [1000 (1.06)] (1.06) + 1000 (1.06)`
  `= 1000 (1.06)^2 + 1000 (1.06)`
`A_3` `= A_2 (1.06) + 1000 (1.06)`
  `= 1000 (1.06)^3 + 1000 (1.06)^2 + 1000 (1.06)`
  `= 1000 [1.06 + 1.06^2 + 1.06^3]`

`vdots`

`A_n =` `1000 [1.06 + 1.06^2 + … + 1.06^n]`
  `text(Note that)  (1.06 + 1.06^2 + … + 1.06^n)\ text(is a)`
  `text(GP where)\ a = 1.06 and r = 1.06`
`:. A_n =` `1000 [(a(r^n – 1))/(r – 1)]`

 

`text(The son’s 18th birthday occurs when)\ n = 18`

`:. A_18` `= 1000 [(1.06 (1.06^18 -1))/(1.06 – 1)]`
  `= 1000 xx 32.7599…`
  `= 32\ 759.991…`
  `= $32\ 760\ \ \ text{(nearest $)}`

 

`:.\ text(The value of Mr Caine’s investment is $32 760.)`

 

ii.  `text(Let)\ V_n = text(value of investment after)\ n\ text(years)`

`V_1` `= 1000 (1.06)`
`V_2` `= V_1 (1.06) + 1000 (1.06) (1.06)`
  `= 1000 (1.06)^2 + 1000 (1.06)^2`
  `= 2000 (1.06)^2`
`V_3` `= V_2 (1.06) + 1000 (1.06)^3`
  `= 2000 (1.06)^3 + 1000 (1.06)^3`
  `= 3000 (1.06)^3`
  `= 3573.048…`
  `= $3573\ \ \ text{(nearest dollar)}`

 

iii.  `text(Continuing the pattern)`

`V_4 = 4000 (1.06)^4`

`vdots`

`V_n = n xx 1000 (1.06)^n`

`:. V_18` `= 18 xx 1000 xx (1.06)^18`
  `= 51\ 378.104…`
  `= $51\ 378\ \ \ text{(nearest dollar)}`

 

`:.\ text(The value of Mrs Caine’s investment on her)`

`text(son’s 18th birthday will be $51 378.)`

Financial Maths, 2ADV M1 2014 HSC 16b

At the start of a month, Jo opens a bank account and makes a deposit of $500.  At the start of each subsequent month, Jo makes a deposit which is 1% more than the previous deposit.

At the end of every month, the bank pays interest of 0.3% (per month) on the balance of the account.  

  1. Explain why the balance of the account at the end of the second month is 

     

      `$500 (1.003)^2 + $500 (1.01) (1.003)`.    (2 marks)

  2. Find the balance of the account at the end of the 60th month, correct to the nearest dollar.     (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `$44\ 404`
Show Worked Solution

i.  `text(Let)\ A_n=text(balance at end of month)\ n`

`A_1` `= 500 (1.003)`
`A_2` `= A_1 (1.003) + 500 (1.01) (1.003)`
  `= 500 (1.003) (1.003) + 500 (1.01)(1.003)`
  `= 500 (1.003)^2 + 500 (1.01) (1.003)`

 

♦ Mean mark 38%
 

ii.  `text(Need to find)\ A_60`

`A_3` `= A_2 (1.003) + 500 (1.01)^2 (1.003)`
  `= [500 (1.003)^2 + 500 (1.01) (1.003)] (1.003)`
  `+ 500 (1.01)^2 (1.003)`
  `= 500 (1.003)^3 + 500 (1.003)^2 (1.01) + 500 (1.003) (1.01)^2`
  `= 500 [1.003 (1.01)^2 + (1.003)^2 (1.01) + (1.003)^3]`

`vdots`

`A_60` `= 500 [1.003 (1.01)^59 + (1.003)^2 (1.01)^58 + … `
  `… + (1.003)^60]`
  `=> text(GP where)\ a = 1.003 (1.01)^59,\ \ r = T_2/T_1=1.003/1.01`
 `:. A_60` `= 500 [ (a(r^n\ – 1))/(r\ – 1)]`
  `= 500 [ (1.003 (1.01)^59 ((1.003/1.01)^60\ – 1))/(1.003/1.01\ – 1) ]`
  `= 500 [ (1.8041057(-0.3411697))/-0.00693069 ]`
  `= 44\ 404.396…`
  `= $44\ 404\ \ text{(nearest dollar)}`

 

`:.\ text(At the end of 60 months, the balance would)`

`text(be)\ $44\ 404.`

Financial Maths, 2ADV M1 2010 HSC 9a

  1. When Chris started a new job, $500 was deposited into his superannuation fund at the beginning of each month. The money was invested at 0.5% per month, compounded monthly. 

     

    Let  `$P`  be the value of the investment after 240 months, when Chris retires.

     

    Show that  `P=232\ 175.55`     (2 marks)

  2. After retirement, Chris withdraws $2000 from the account at the end of each month, without making any further deposits. The account continues to earn interest at 0.5% per month.

     

    Let  `$A_n`  be the amount left in the account  `n`  months after Chris's retirement.

     

      (1)  Show that  `A_n=(P-400\ 000)xx1.005^n+400\ 000`.     (3 marks)

     

      (2)  For how many months after retirement will there be money left in the account?     (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. (1)  `text{Proof (See Worked Solutions)}`
  3. (2)  `text(175 months)`
Show Worked Solutions
i.     `P_1` `=500(1.005)`
`P_2` `=500(1.005^2)+500(1.005^1)`
`P_3` `=500(1.005^3+1.005^2+1.005)`
  `vdots`
`P_240` `=500(1.005+1.005^2+1.005^3 …+1.005^240)`

 

`=>\ text(GP where)\ \ a=1.005,\ text(and)\ \ r=1.005`

MARKER’S COMMENT: Common errors included using `r=1.05`, and taking the first term of the GP as 1 instead of 1.005 (note that the $500 goes in at the start of the month and earns interest before it is included in `$P_n`).
`P_240` `=500((a(r^n-1))/(r-1))`
  `=500((1.005(1.005^240-1))/(1.005-1))`
  `=100\ 000[1.005(1.005^240-1)]`
  `=232\ 175.55`

 

`:.\ text(The value of Chris’ investment after 240 months)`

`text(is) \ $232\ 175.55 text(  … as required)`

 

ii. (1)  `text(After 1 month,)\  A_1=P(1.005)-2000`

IMPORTANT: At the end of the month, `$P` earns interest for the month BEFORE any withdrawal is made. Many students mistakenly had `$A_1=(P-2000)(1.005)`.
`A_2` `=A_1(1.005)-2000`
  `=[P(1.005)-2000](1.005)-2000`
  `=P(1.005^2)-2000(1.005)-2000`
  `=P(1.005^2)-2000(1+1.005)`
  ` vdots`
`A_n` `=P(1.005^n)-2000(1+1.005+…+1.005^(n-1))`

`=>\ text(GP where)\ \ a=1\ \ text(and)\ \ r=1.005`

`A_n` `=P(1.005^n)-2000((1(1.005^n-1))/(1.005-1))`
  `=P(1.005^n)-400\ 000(1.005^n-1)`
  `=P(1.005^n)-400\ 000(1.005^n)+400\ 000`
  `=(P-400\ 000)xx1.005^n+400\ 000\ \ text(… as required)`

 

ii. (2)  `text(Find)\ n\ text(such that)\ A_n<=0`

♦ Mean mark 38%

`text(S)text(ince)\  P=232\ 175.55`,

`(232\ 175.55-400\ 000)(1.005^n)+400\ 000<=0`

`167\ 824.45(1.005^n)` `>=400\ 000`
`1.005^n` `>=(400\ 000)/(167\ 824.45)`
`n ln1.005` `>=ln2.383443`
`n` `>=ln2.383443/ln1.005`
`n` `>=174.14\ \ text{(to 2 d.p.)}`

 

`:.\ text(There will be money left in the account for 175 months.)`

Financial Maths, 2ADV M1 2011 HSC 8c

When Jules started working she began paying $100 at the beginning of each month into a superannuation fund.

The contributions are compounded monthly at an interest rate of 6% per annum.

She intends to retire after having worked for 35 years.

  1. Let  `$P`  be the final value of Jules's superannuation when she retires after 35 years (420 months). Show that  `$P=$143\ 183`  to the nearest dollar.     (2 marks)

  2. Fifteen years after she started working Jules read a magazine article about retirement, and realised that she would need `$800\ 000` in her fund when she retires. At the time of reading the magazine article she had `$29\ 227` in her fund. For the remaining 20 years she intends to work, she decides to pay  `$M`  into her fund at the beginning of each month. The contributions continue to attract the same interest rate of 6% per annum, compounded monthly.

  3.  

    At the end of  `n`  months after starting the new contributions, the amount in the fund is  `$A_n`.

  4.  

      (1)  Show that  `A_2=29\ 227xx1.005^2+M(1.005+1.005^2)`.     (1 mark)

  5.  

      (2)  Find the value of  `M`  so that Jules will have $800 000 in her fund after the remaining 20 years (240 months).     (3 marks)

Show Answers Only
  1.  `text{Proof (See Worked Solutions)}`
  2. (1) `text{Proof (See Worked Solutions)}`
    (2) `$1514.48\ text{(nearest cent)}`
Show Worked Solutions
i.    `P_1` `=Pxxr=Pxx(1+(6%)/12)=100(1.005)`
  `P_2` `=P_1(1.005)+100(1.005^1)`
    `=100(1.005^2)+100(1.005^1)`
    `=100(1.005^2+1.005)`
  `P_3` `=(1.005)[100(1.005^2+1.005)]+100(1.005)`
    `=100(1.005+1005^2+1.005^3)`
    `\ \ \ \ vdots`
  `P_420` `=100(1.005+1.005^2+1.005^3 …+1.005^420)`

`=>\ text(GP where)\ \ a=1.005,\ \ r=1.005`

MARKER’S COMMENT: Common errors in this part included having the first term of the GP as 1 instead of 1.005 (note that the $100 goes in at the start of the month and earns interest before it is included in `$P_n)`.
`P_420` `=100((a(r^n-1))/(r-1))`
  `=100((1.005(1.005^420-1))/(1.005-1))`
  `=20\ 000(1.005(1.005^420-1))`
  `=$143\ 183.39`

 

`:.\ text{The final value of Jules’s superannuation is}`

`$143\ 183\ \ text{(to the nearest dollar)   … as required}`

 

♦ Mean mark 34% for part (ii)(1)

ii. (1)  `text(After 1 month,)\  A_1=29\ 227(1.005)+M(1.005)`

`A_2` `=A_1 (1.005)+M(1.005)`
  `=[29\ 227(1.005)+M(1.005)](1.005)+M(1.005)`
  `=29\ 227(1.005^2)+M(1.005^2)+M(1.005)`
  `=29\ 227(1.005^2)+M(1.005+1.005^2)\ \ text(… as required)`

 

ii. (2)  `text(Find)\ $M\ text(such that)\  A_n=$800\ 000\ text(after 240 months.)`

♦ Mean mark 49%

`A_240=29\ 227(1.005^240)+M(1.005+1.005^2+..+1.005^240)`

`=>\ GP\ text(where)\ a=1.005,\ text(and)\ r=1.005`

`800\ 000=29\ 227(1.005^240)+M((1.005(1.005^240-1))/(1.005-1))`

`M((1.005(1.005^240-1))/(1.005-1))=800\ 000-29\ 227(1.005^240)`

`M` `=(703\ 252.65)/(464.3511)`
  `=1514.484`..
`:.M` `=$1514.48\ \ text{(to the nearest cent)}`