SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

PHYSICS, M5 2024 HSC 30

An object sits on the floor of a hollow cylinder rotating around an axis, as shown. The cylinder's rotation causes the object to undergo uniform circular motion.
 

Explain the effect on all of the forces acting on the object if the period of the cylinder's rotation is halved. Ignore the effects of friction.   (4 marks)

Show Answers Only

Forces acting on the object:

  • The gravitational force pulls the object straight down toward Earth
  • The floor provides an upward force that pushes back against gravity
  • A centripetal force acts inward from the cylinder’s wall, directing the object toward the centre of the cylinder

Consider the centripetal force:

   \(F_C = \dfrac{mv^{2}}{r}=\dfrac{m}{v} \Big( \dfrac{2\pi r}{T} \Big)^{2} = \dfrac{4m \pi^{2} r}{T^{2}}\)

  • When the period is cut in half \((T \rightarrow \frac{T}{2})\), the centripetal force becomes four times stronger.
  • The other forces, gravity pulling down and the floor pushing up, stay the same since they aren’t affected by how quickly the object moves in its circular path (i.e. its period).

Show Worked Solution

Forces acting on the object:

  • The gravitational force pulls the object straight down toward Earth
  • The floor provides an upward force that pushes back against gravity
  • A centripetal force acts inward from the cylinder’s wall, directing the object toward the centre of the cylinder

Consider the centripetal force:

   \(F_C = \dfrac{mv^{2}}{r}=\dfrac{m}{v} \Big( \dfrac{2\pi r}{T} \Big)^{2} = \dfrac{4m \pi^{2} r}{T^{2}}\)

  • When the period is cut in half \((T \rightarrow \frac{T}{2})\), the centripetal force becomes four times stronger.
  • The other forces, gravity pulling down and the floor pushing up, stay the same since they aren’t affected by how quickly the object moves in its circular path (i.e. its period).

PHYSICS, M5 2019 VCE 8

A 250 g toy car performs a loop in the apparatus shown in the diagram below.
 

The car starts from rest at point \(\text{A}\) and travels along the track without any air resistance or retarding frictional forces. The radius of the car's path in the loop is 0.20 m. When the car reaches point \(\text{B}\) it is travelling at a speed of 3.0 m s\(^{-1}\).

  1. Calculate the value of \(h\). Show your working.   (3 marks)

  2. Calculate the magnitude of the normal reaction force on the car by the track when it is at point \(\text{B}\). Show your working.   (3 marks)

  3. Explain why the car does not fall from the track at point \(\text{B}\), when it is upside down.   (2 marks)

Show Answers Only

a.    \(0.86\ \text{m}\)

b.    \(8.8\ \text{N}\)

c.    Method 1

  • During the car’s circular motion around the loop, the magnitude of the centripetal force exceeds the magnitude of the weight force.
  • This produces a normal reaction force acting downwards which enables the car to travel around the loop at 3 ms\(^{-1}\).

Method 2

  • The minimum speed required for the car so that it stays on the track will be when the centripetal force is equal to the weight force. 
\(\dfrac{mv^2}{r}\) \(=mg\)  
\(v\) \(=\sqrt{gr}=\sqrt{9.8 \times 0.2}=1.4\ \text{ms}^{-1}\)  

 

  • As 3 ms\(^{-1}\) is greater than the minimum speed required, a normal force downwards will be present at point \(\text{B}\).
  • Therefore the car will not fall from the track at point \(\text{B}\).

Show Worked Solution

a.    Using the law of the conservation of energy:

\(mgh_A\) \(=mgh_B +\dfrac{1}{2}mv^2_b\)  
\(0.25 \times 9.8 \times h_A\) \(=0.25 \times 9.8 \times 0.4 + \dfrac{1}{2} \times 0.25 \times 3^2\)  
\(2.45h_A\) \(=2.105\)  
\(h_A\) \(=\dfrac{2.105}{2.45}=0.86\ \text{m}\)  

 

b.     \(N + mg\) \(=\dfrac{mv^2}{r}\)
  \(N\) \(=\dfrac{mv^2}{r}-mg\)
    \(=\dfrac{0.25 \times 3^2}{0.2}- 0.25 \times 9.8\) 
    \(=8.8\ \text{N}\)

♦ Mean mark (b) 53%.

c.    Method 1

  • During the car’s circular motion around the loop, the magnitude of the centripetal force exceeds the magnitude of the weight force.
  • This produces a normal reaction force acting downwards which enables the car to travel around the loop at 3 ms\(^{-1}\).

Method 2

  • The minimum speed required for the car so that it stays on the track will be when the centripetal force is equal to the weight force. 
\(\dfrac{mv^2}{r}\) \(=mg\)  
\(v\) \(=\sqrt{gr}=\sqrt{9.8 \times 0.2}=1.4\ \text{ms}^{-1}\)  

  • As 3 ms\(^{-1}\) is greater than the minimum speed required, a normal force downwards will be present at point \(\text{B}\).
  • Therefore the car will not fall from the track at point \(\text{B}\).
♦♦♦ Mean mark (c) 23%.
COMMENT: Normal force is poorly understood here..

PHYSICS, M5 2020 VCE 8

The diagram below shows a small ball of mass 1.8 kg travelling in a horizontal circular path at a constant speed while suspended from the ceiling by a 0.75 m long string.
 


 

  1. Use labelled arrows on the diagram above to indicate the two physical forces acting on the ball.   (2 marks)
  1. Calculate the speed of the ball. Show your working.   (4 marks)
Show Answers Only

a.  
       

b.    \(1.2\ \text{ms}^{-1}\)

Show Worked Solution

a.    Only two forces are acting on the ball: \(F_w\) and \(F_T\):
 

   

Mean mark 58%.
COMMENT: Many students incorrectly identified centripetal force (this is a result of the tension force).

b.   
     

\(\text{Using}\ \ \tan\theta=\dfrac{F_{\text{net}}}{mg}:\)

\( F_{\text{net}}\) \(=mg\,\tan\theta\)  
\(\dfrac{mv^2}{r}\) \(=mg\,\tan\theta\)  
\(\dfrac{v^2}{r}\) \(=g\,\tan\theta\)  
\(\therefore v\) \(=\sqrt{g\,r\,\tan\theta}\)  
  \(=\sqrt{9.8 \times 0.317 \times \tan 25}\ \ ,\ \ (r = 0.75 \times \sin25=0.317\ \text{m})\)  
  \(=1.2\ \text{ms}^{-1}\)  
♦ Mean mark (b) 50%.

PHYSICS, M5 2023 HSC 32

A horizontal disc rotates at 3 revolutions per second around its centre, with the top of the disc at ground level.

At 2 m from the centre of the disc, a ball is held in place at ground level on the top of the disc by a spring-loaded projectile launcher. At position \(X\), the launcher fires the ball vertically upward with a velocity of 5.72 m s\(^{-1}\).
 


 

Calculate the ball's position relative to the launcher's new position, at the instant the ball hits the ground.   (7 marks)

Show Answers Only

The position of the ball relative to the launcher’s new position is 44.19 m, 5.2\(^{\circ}\) below the horizontal line of the launcher.

Show Worked Solution

Find horizontal velocity of the ball, \(v_{\text{x}}\):

\(T=\dfrac{1}{3} = 0.333\ \text{seconds} \)

\(v_{\text{x}}=\dfrac{2\pi r}{T}=\dfrac{2\pi \times 2}{0.333…}=37.699\ \text{ms}^{-1}\)

♦ Mean mark 53%.

Calculating the time of flight, \(t_1\):

Let  \(t_2\) = time to max height

\(v_{\text{y}}\) \(=u_{\text{y}} + at_2\)  
\(t_2\) \(=\dfrac{v_{\text{y}}-u_{\text{y}}}{a}=\dfrac{0-5.72}{-9.8}=0.58367\ \text{sec} \)  

 

Time of flight (\(t_1)= 2 \times t_2= 1.167\ \text{s}\)
 

Range of the ball from launch position:

\(s_{\text{x}}=v_{\text{x}} \times t_2=37.699 \times 1.167=44.0\ \text{m}\)
 

Position of the launcher (L) when the ball hits the ground:

  • Revolutions (before ball lands) = 3 × 1.167 = 3.5 revolutions
  • The Launcher (L) is \(\frac{1}{2}\) a revolution past its starting point.
  • Thus, the positions of both the ball and the launcher at the time when the ball hits the ground can be demonstrated in the diagram below.
     

 

\(D\) \(=\sqrt{44.0^2+4^2}=44.18\ \text{m}\)  
\(\theta\) \(=\tan ^{-1}\left(\dfrac{4}{44.0}\right)=5.2^{\circ}\)  

 

  • The final position of the ball relative to \(L\) is 44.18 m, 5.2\(^{\circ}\) below the horizontal line at \(L\).

PHYSICS, M5 2015 HSC 26

Consider the following two models used to calculate the work done when a 300 kg satellite is taken from Earth's surface to an altitude of 200 km.

You may assume that the calculations are correct.
 

  1. What assumptions are made about Earth's gravitational field in models `X` and `Y` that lead to the different results shown?   (2 marks)
  1. Why do models `X` and `Y` produce results that, although different, are close in value?   (1 mark)
  1. Calculate the orbital velocity of the satellite in a circular orbit at the altitude of 200 km.   (3 marks)
Show Answers Only

a.  Model `X`:

  • Assumes Earth’s gravitational field strength remains constant moving upwards from the surface.

Model `Y`:

  • Assumes Earth’s gravitational field strength changes with altitude.

b.   Similarity of results due to:

  • The variation in gravitational field strength from Earth’s surface to an altitude of 200 km is minimal, so both models `X` and `Y` produce similar results.

c.   `v=7797  text{ms}^(-1)`

Show Worked Solution

a.  Model `X`:

  • Assumes Earth’s gravitational field strength remains constant moving upwards from the surface.

Model `Y`:

  • Assumes Earth’s gravitational field strength changes with altitude.

♦ Mean mark (a) 54%.

b.   Similarity of results due to:

  • The variation in gravitational field strength from Earth’s surface to an altitude of 200 km is minimal, so both models `X` and `Y` produce similar results.

♦♦ Mean mark (b) 38%.

c.    Centripetal force = force due to gravity:

`F_(c)` `=F_(g)`  
`(mv^2)/(r)` `=(GMm)/(r^2)`  
`:.v` `=sqrt((GM)/(r))=sqrt((6.67 xx10^(-11)xx6xx10^(24))/(6.58 xx10^(6)))=7797  text{ms}^(-1)`  

PHYSICS, M5 2015 HSC 11 MC

Which of the following diagrams correctly represents the force(s) acting on a satellite in a stable circular orbit around Earth?
 

 

Show Answers Only

`D`

Show Worked Solution
  • In a stable, circular orbit the satellite requires no propulsion force to keep it in orbit. This is due to it undergoing uniform circular motion with gravity acting as its centripetal force.
  • A force of gravity acts on the satellite, with direction towards Earth’s centre of mass. 
  • No ‘reaction force’ acts on the satellite. This is because any ‘reaction’ to the gravitational force exerted on the satellite by the Earth is an equal and opposite force exerted on the Earth by the satellite (Newton’s Third Law).
  • i.e. The reaction force acts on the Earth, not the satellite.

`=>D`


♦♦♦ Mean mark 29%.

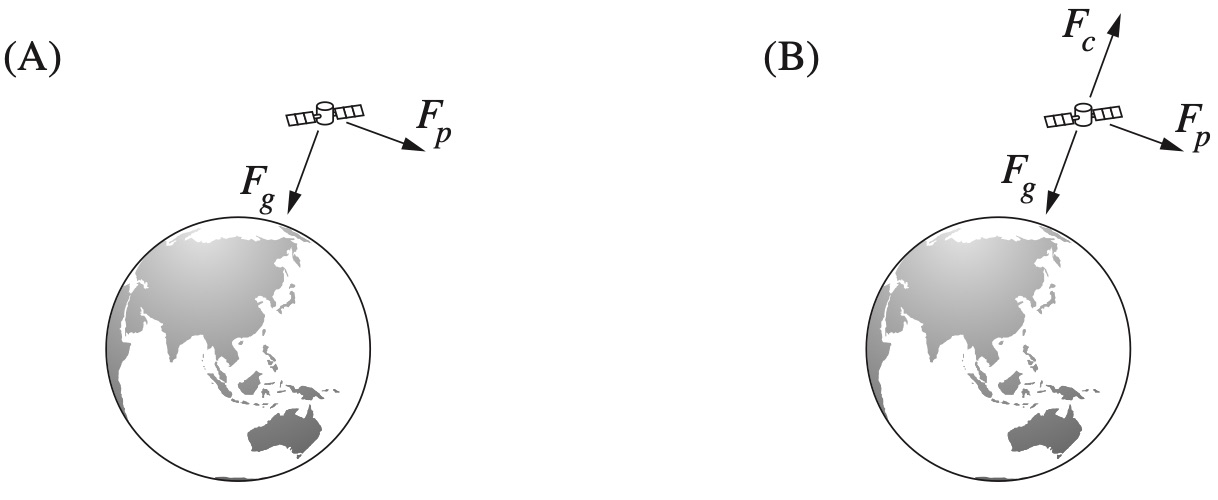
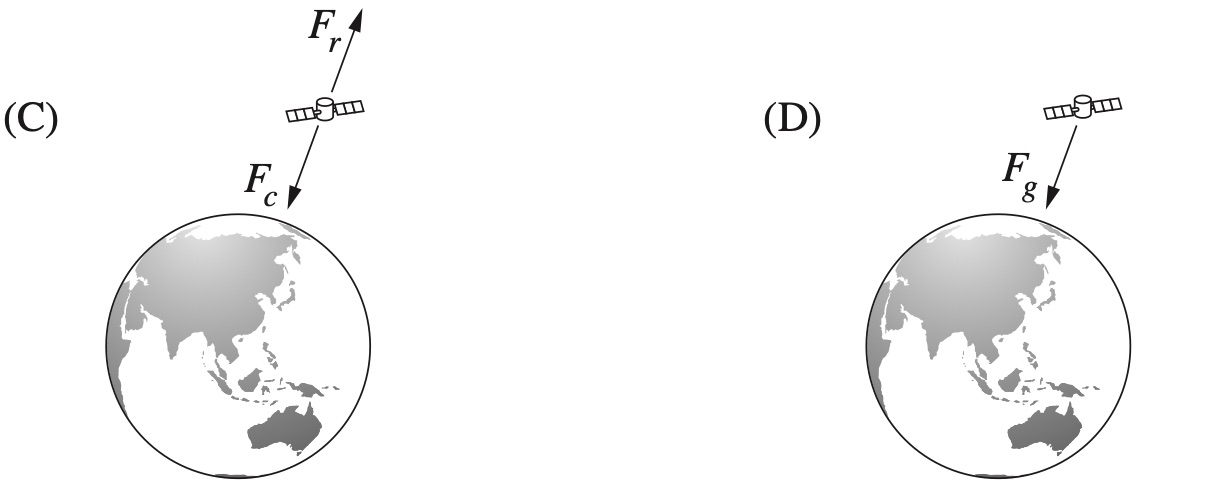
PHYSICS, M5 2019 HSC 35

The apparatus shown is attached horizontally to the roof inside a stationary car. The plane of the protractor is perpendicular to the sides of the car.
 

The car was then driven at a constant speed `(v)`, on a horizontal surface, causing the string to swing to the right and remain at a constant angle `(theta)` measured with respect to the vertical.

Describe how the apparatus can be used to determine features of the car's motion. In your answer, derive an expression that relates a feature of the car's motion to the angle `theta`.   (4 marks)

Show Answers Only
  • The constant deflection of the mass to the right indicates that the car has a uniform acceleration to the left.
  • Since the car’s speed is constant, it must be travelling in uniform circular motion.
  • The radius of the car’s motion can be found in terms of `theta.`

As there is no vertical acceleration of the mass, the vertical component of its tension will balance its weight:

`T_y=Tcos theta=mg\ \ …\ (1)`

The centripetal force on the mass is given by the horizontal component of its tension:

`T_x=Tsin theta=ma=(mv^2)/r\ \ …\ (2)`

Substitute `T=(mg)/costheta`  from `(1)` into `(2)`:

`T sin theta` `=(mv^2)/(r)`
`(mg xx sin theta)/(cos theta)` `=(mv^(2))/(r)`
`g xx tan theta` `=(v^(2))/(r)`
`r` `=(v^(2))/(g xx tan theta)`

 
Other expressions could include:

  • `v=sqrt(rg tan theta)`
Show Worked Solution
  • The constant deflection of the mass to the right indicates that the car has a uniform acceleration to the left.
  • Since the car’s speed is constant, it must be travelling in uniform circular motion.
  • The radius of the car’s motion can be found in terms of `theta.`

As there is no vertical acceleration of the mass, the vertical component of its tension will balance its weight:

`T_y=Tcos theta=mg\ \ …\ (1)`

The centripetal force on the mass is given by the horizontal component of its tension:

`T_x=Tsin theta=ma=(mv^2)/r\ \ …\ (2)`

Substitute `T=(mg)/costheta`  from `(1)` into `(2)`:

`T sin theta` `=(mv^2)/(r)`
`(mg xx sin theta)/(cos theta)` `=(mv^(2))/(r)`
`g xx tan theta` `=(v^(2))/(r)`
`r` `=(v^(2))/(g xx tan theta)`

 
Other expressions could include:

  • `v=sqrt(rg tan theta)`

♦ Mean mark 52%.