SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

ENGINEERING, CS 2024 HSC 21c

Strap bracing is used in the construction of many residential structures. It has holes punched along its length to allow tensioners to be applied as shown.
 

A 6 mm diameter hole is to be punched into mild steel strap bracing.

If the shear strength of the bracing is 380 MPa and the shear force required to punch the hole is 5.73 kN, what is the maximum allowable thickness of the strap bracing?   (3 marks)

Show Answers Only

Show Worked Solution

 
 
 
   

 

 
 
   
   
   

ENGINEERING, CS 2023 HSC 26a

A component of a roller coaster car bogie is to be punched out from a 10 mm thick rectangular plate of mild steel as shown.
 

Calculate the shear force of the punching die if the shear stress is 345 MPa.   (3 marks)

Show Answers Only

Show Worked Solution

 
   
   
 
   
   
   
♦ Mean mark 43%.

ENGINEERING, PPT 2016 HSC 24d

A mild steel nut and bolt is used to hold a bumper bar onto the chassis of a truck. The bolt needs to withstand a maximum shear load of 2 kN.
 

If the maximum shear stress of the material is 56 MPa and the factor of safety is 2, calculate the minimum bolt diameter.   (3 marks)

Show Answers Only

Show Worked Solution

 
 
 
 
   
   
 
   

Mean mark 55%.

ENGINEERING, AE 2017 HSC 26b

Orthogonal and pictorial drawings of a sheet metal electrical cable cover are given below.
 

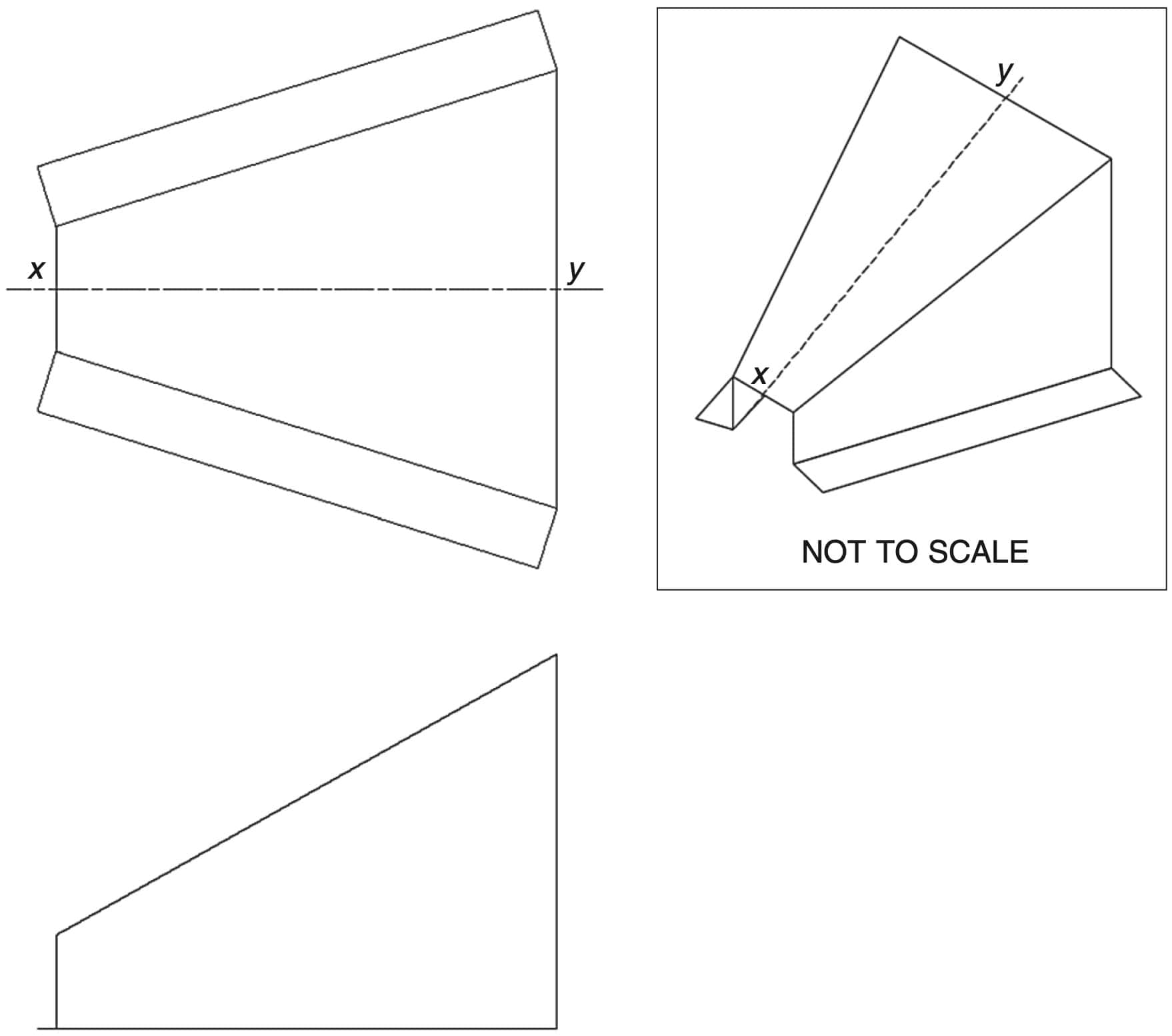
  1. Draw a half-development of the electrical cable cover. Use the centre line to position the development.   (4 marks)
     

  1. A 20 mm diameter hole is to be punched through the top of the electrical cable cover before folding.
  2. The ultimate shear stress of the material used to manufacture the cover is 110 MPa.
  3. Calculate the force required to punch out the hole if the thickness of the sheet metal is 0.5 mm.   (3 marks)
Show Answers Only

i.   
         

ii.   

Show Worked Solution

i.   
         

Key Points for this Drawing:

  • Find true length of each line from the diagrams given
  • Do not dimension
  • Only complete a half development, not a full development
  • Use lighter lines for the the bends/folds and heavier lines for the outline
  • Label all points
ii.   
 

 

 
   
   

♦ Mean mark (ii) 42%.

ENGINEERING, CS 2019 HSC 27bi

The bracket and lock pin assembly shown is used to attach the repeater transmitters to the tower.
 

Using the data given, determine the minimum lock pin diameter to use.   (3 marks)
 

Show Answers Only

Show Worked Solution

 
 
 
   

 

 
 
   
   

   


♦♦♦ Mean mark 30%.

ENGINEERING, CS 2020 HSC 24c

The photograph shows a turnbuckle and yoke secured by a pin.
 

   

The diameter of the pin in the turnbuckle is 40 mm and the shear stress across this pin is 55 MPa.

Find the magnitude of the axial load on the turnbuckle.   (3 marks)

Show Answers Only

Show Worked Solution

Ø

 
 
   
   
   

 
However, the system is in double shear, therefore:

 
   
   

♦ Mean mark 47%.