smc-624-20-Cost

NETWORKS, FUR2 2017 VCAA 1

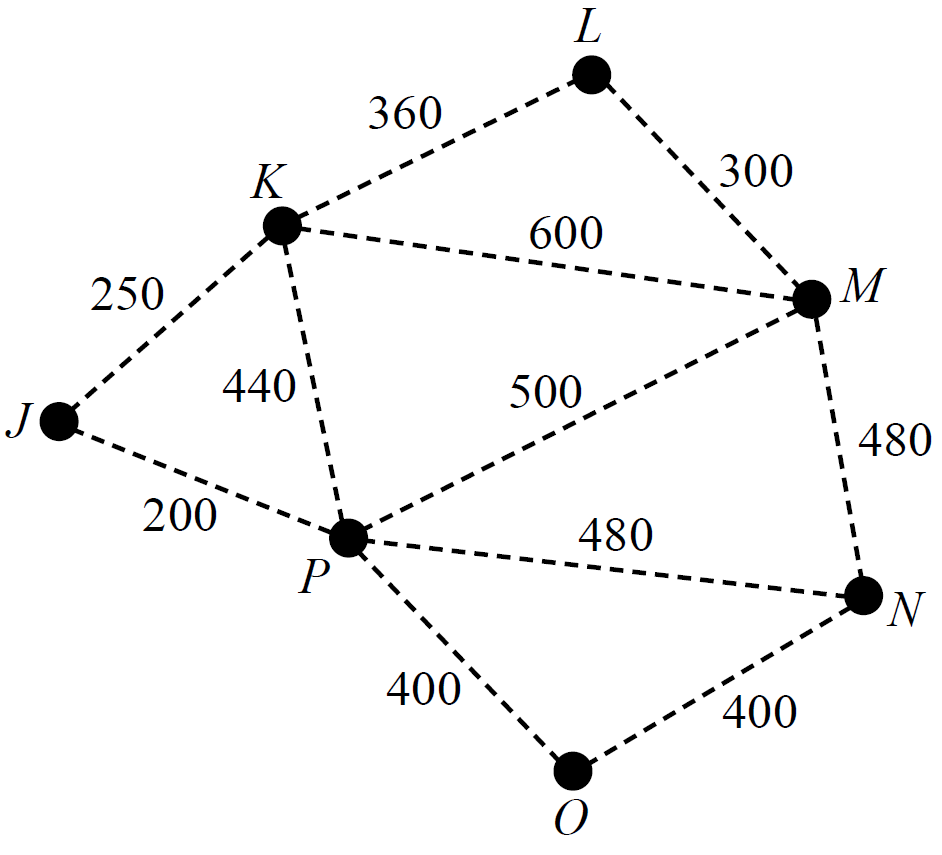
Bus routes connect six towns.

The towns are Northend (`N`), Opera (`O`), Palmer (`P`), Quigley (`Q`), Rosebush (`R`) and Seatown (`S`).

The graph below gives the cost, in dollars, of bus travel along these routes.

Bai lives in Northend (`N`) and he will travel by bus to take a holiday in Seatown (`S`).

Bai considers travelling by bus along the route Northend (`N`) – Opera (`O`) – Seatown (`S`).

How much would Bai have to pay? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
If Bai takes the cheapest route from Northend (`N`) to Seatown (`S`), which other town(s) will he pass through? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Euler’s formula, `v + f = e + 2`, holds for this graph.
Complete the formula by writing the appropriate numbers in the boxes provided below. (1 mark)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

a. `$120`

b. `text(Quigley and Rosebush.)`

Show Worked Solution

a.	`text(C)text(ost)`	`= 15 + 105`
		`= $120`

b. `text(Cheapest route is)\ N – Q – R – S`

`:.\ text(Other towns are Quigley and Rosebush.)`

The vertices of the graph above represent nine computers in a building. The computers are to be connected with optical fibre cables, which are represented by edges. The numbers on the edges show the costs, in hundreds of dollars, of linking these computers with optical fibre cables.

Based on the same set of vertices and edges, which one of the following graphs shows the cable layout (in bold) that would link all the computers with optical fibre cables for the minimum cost?

Show Answers Only

`A`

Show Worked Solution

`=> A`

NETWORKS, FUR2 2015 VCAA 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.

The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

What is the cost, in dollars, of installing the cable between server `L` and server `M`? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`? (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
An inspector checks the cables by walking along the length of each cable in one continuous path.
To avoid walking along any of the cables more than once, at which vertex should the inspector start and where would the inspector finish? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.
i. The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

Draw the minimum spanning tree on the plan below? (1 mark)

--- 0 WORK AREA LINES (style=lined) ---
ii. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven.

How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?
A copy of the graph above is provided below to assist with your working. (1 mark)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`$300`
`$920`
`N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
i.

d.ii.`$120`

Show Worked Solution

a. `$300`

b. `text(C)text(ost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`

c. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.

d.i.

d.ii. `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)`	`= 600 – 480`
	`= $120`