SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, STD2 N2 SM-Bank 10

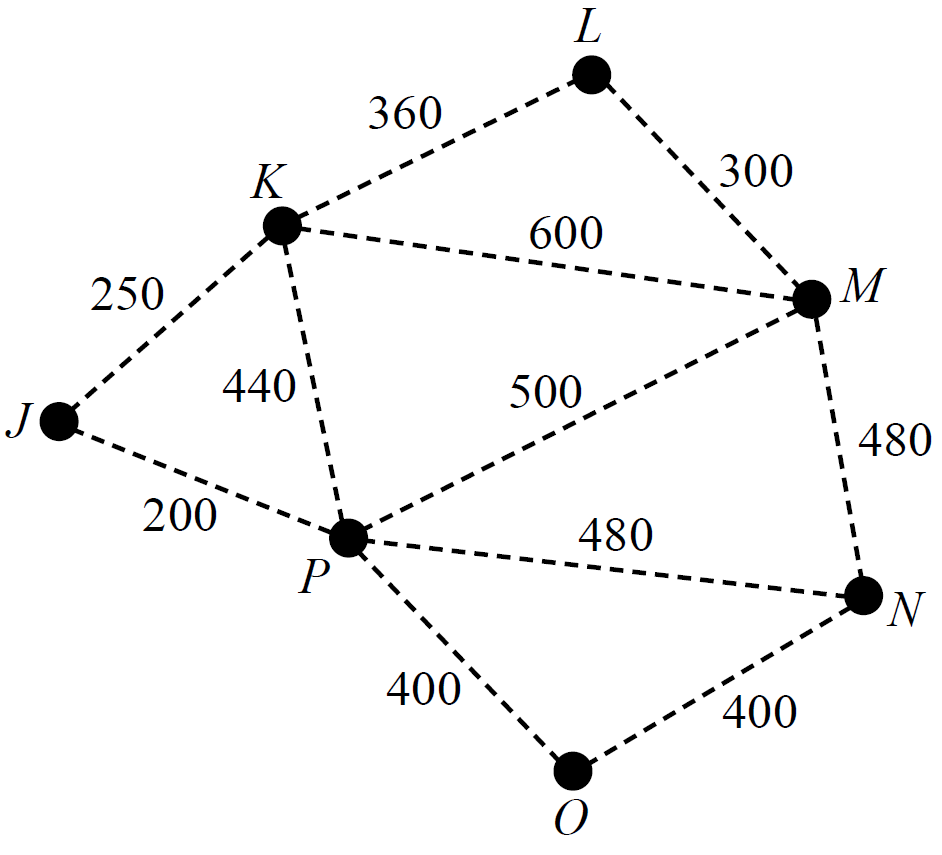
The vertices of the graph below represent cabins in a holiday park, and the water pump \((P)\) that will supply them. The numbers on the edges show the length, in metres, of water pipe required to connect the cabins and the pump.
 

The water pipes will cost $52 per metre. 

Determine the minimum cost to link all the cabins to the water pump \((P)\).   (3 marks)

Show Answers Only

\(\text{Minimum cost}\ = 73 \times 52=\$3796\)

Show Worked Solution

Minimum spanning tree:
 

\(\text{MST}\ =8+9+11+8+9+9+7+12=73\)

\(\therefore\ \text{Minimum cost}\ = 73 \times 52=\$3796\)

Networks, STD2 N2 SM-Bank 2

A school is designing a computer network between five key areas within the school.

The cost of connecting the rooms is shown in the diagram below.
  


 

  1. Complete the spanning tree below that creates the school's network at a minimum cost.  (1 mark)
      


     
     

  2. What is the minimum cost of the network?  (1 mark)

Show Answers Only
  1.  
         
     
  2. `$1500`
Show Worked Solution

i.   `text(One Strategy: Using Prim’s Algorithm)`

`text(Starting vertex – Staff Room)`

`text(1st edge: Staff Room – Library)`

`text(2nd edge: Library – School Office)`

`text(3rd edge: Staff Room – IT Staff)`

`text(4th edge: Library – Computer Room)`
  

 

ii.    `text(Minimum Cost)` `= 300 + 300 + 400 + 500`
    `= $1500`

Networks, STD2 N2 2015 FUR2 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
 

Networks, FUR2 2015 VCAA 11

 
The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

  1. What is the cost, in dollars, of installing the cable between server `L` and server `M`?  (1 mark)

  2. What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`?  (1 mark)

  3. The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.

    1. The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

       

      Draw the minimum spanning tree on the plan below.  (1 mark) 
       

      Networks, FUR2 2015 VCAA 12
       

    2. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven.

       

      How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?

       

      A copy of the graph above is provided below to assist with your working.  (1 mark)

      Networks, FUR2 2015 VCAA 12

Show Answers Only
  1. `$300`
  2. `$920`
  3. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
    1.  
      Networks, FUR2 2015 VCAA 12 Answer
    2. `$120`
Show Worked Solution

a.   `$300`

 

b.   `text(Minimum cost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`
 

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.

c.i.  `text(Using Prim’s Algorithm:)`

`text(Starting at Vertex)\ L`

`text{1st Edge: L → M (300)}`

`text{2nd Edge: L → K (360)}`

`text{3rd Edge: K → J (250)}`

`text{4th Edge: J → P (200)  etc…}`
 

Networks, FUR2 2015 VCAA 12 Answer


c.ii.   `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)` `= 600 – 480`
  `= $120`