The container shown is initially full of water.
Water leaks out of the bottom of the container at a constant rate.
Which graph best shows the depth of water in the container as time varies?
| A. |  |
B. |  |
| C. |  |
D. |  |
Algebra, STD2 A4 2007 HSC 27a
A rectangular playing surface is to be constructed so that the length is 6 metres more than the width.
- Give an example of a length and width that would be possible for this playing surface. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Write an equation for the area (`A`) of the playing surface in terms of its length (`l`). (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
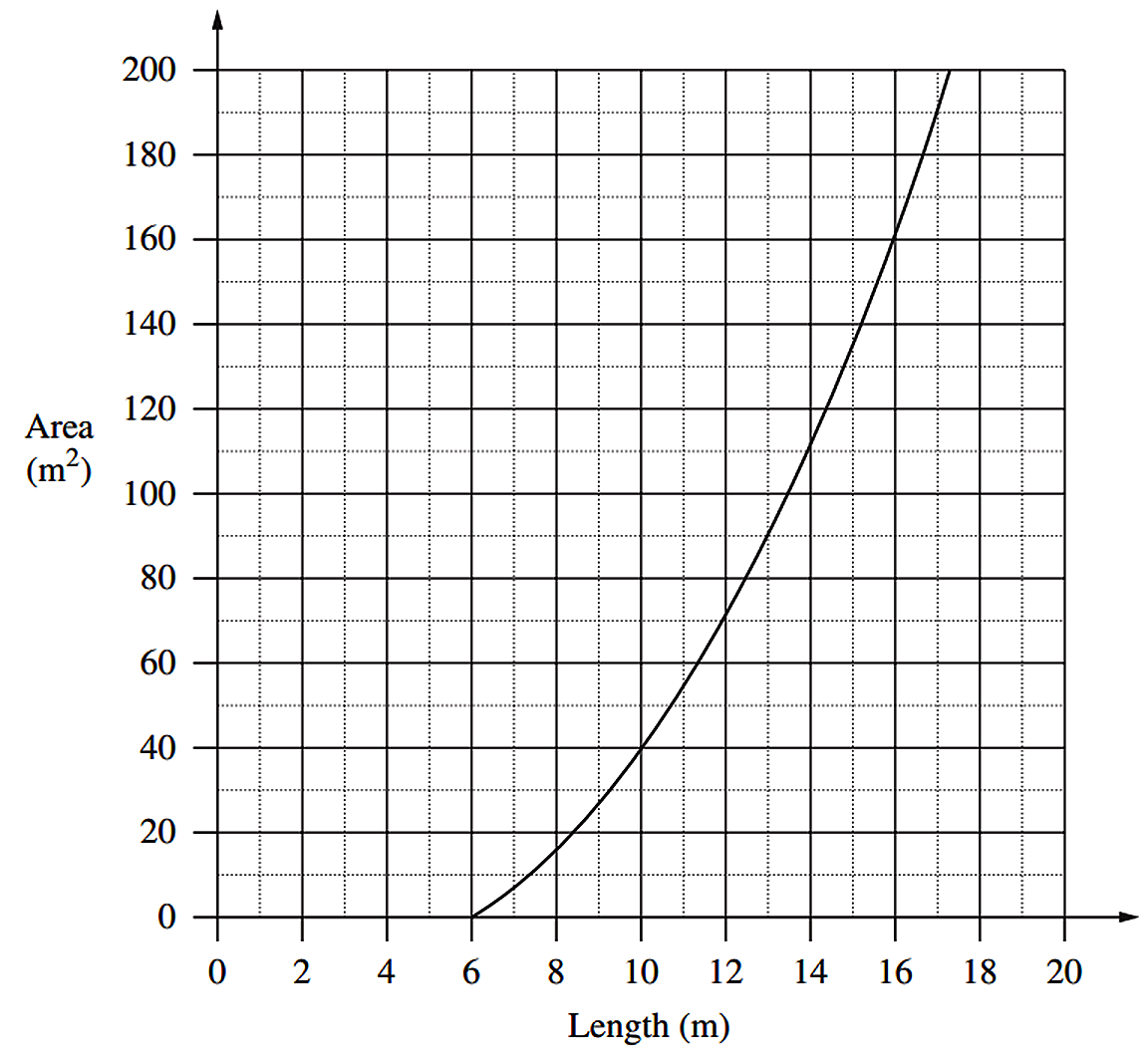
A graph comparing the area of the playing surface to its length is shown.
- Why are lengths of 0 metres to 6 metres impossible? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- What would be the dimensions of the playing surface if it had an area of 135 m²? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
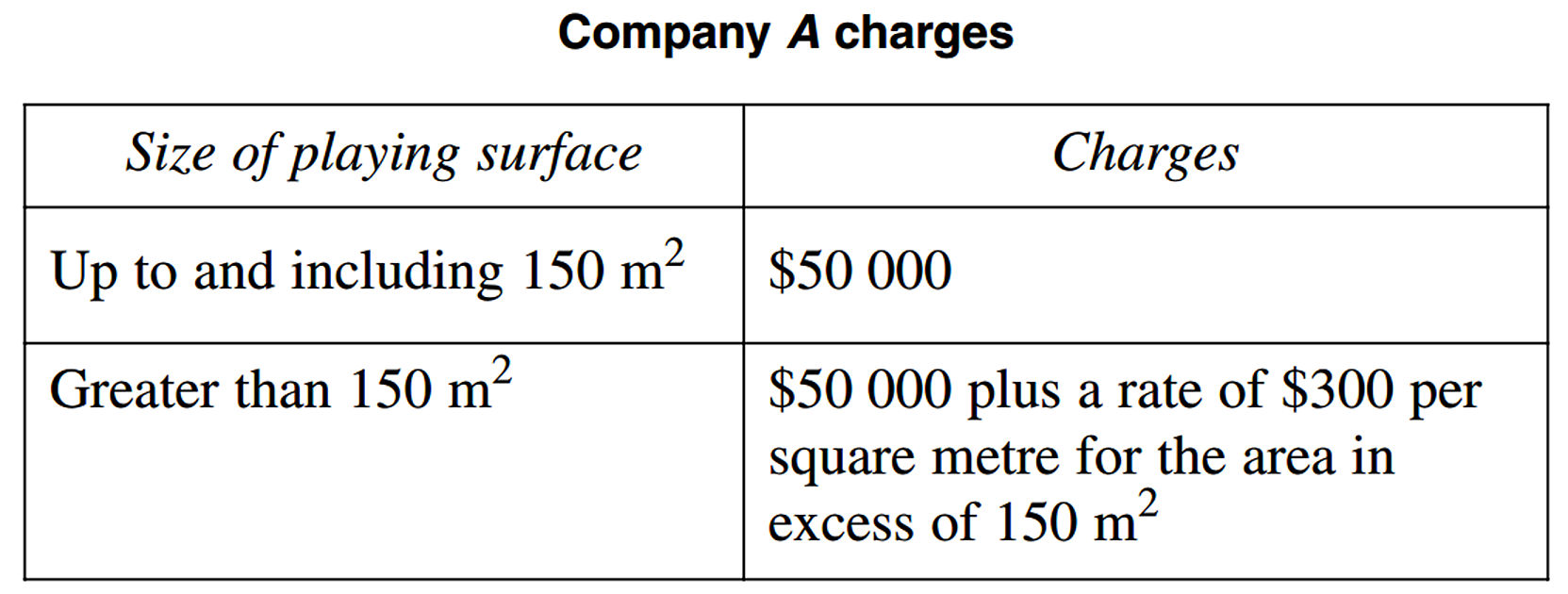
Company `A` constructs playing surfaces.
- Draw a graph to represent the cost of using Company `A` to construct all playing surface sizes up to and including 200 m².
Use the horizontal axis to represent the area and the vertical axis to represent the cost. (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Company `B` charges a rate of $360 per square metre regardless of size.
- Which company would charge less to construct a playing surface with an area of 135 m²
Justify your answer with suitable calculations. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Answers Only
- `text(One possibility is a length of 10 m, and a width)`
`text{of 4 m (among many possibilities).}`
- `A = l (l – 6)\ \ text(m²)`
- `text(Given the length must be 6 m more than)`
`text(the width, it follows that the length)`
`text(must be greater than 6 m.)`
- `text(15 m × 9 m)`
-
- `text(Proof)\ \ text{(See worked solutions)}`
Show Worked Solution
i. `text(One possibility is a length of 10 m, and a width)`
`text{of 4 m (among many possibilities).}`
ii. `text(Length) = l\ text(m)`
`text(Width) = (l – 6)\ text(m)`
| `:.\ A` | `= l (l – 6)` |
iii. `text(Given the length must be 6m more than the width,)`
`text(it follows that the length must be greater than 6 m)`
`text(so that the width is positive.)`
iv. `text(From the graph, an area of 135 m² corresponds to)`
`text(a length of 15 m.)`
`:.\ text(The dimensions would be 15 m × 9 m.)`
| v. |  |
vi. `text(Company)\ A\ text(cost) = $50\ 000`
| `text(Company)\ B\ text(cost)` | `= 135 xx 360` |
| `= $48\ 600` |
`:.\ text(Company)\ B\ text(would charge $1400 less)`
`text(than Company)\ A.`
Algebra, STD2 A4 2013 HSC 27a
Lucy went for a bike ride. She left home at 8 am and arrived back at home at 6 pm. A graph representing her journey is shown.
- What was the total distance that she rode during the day? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- How much time did Lucy spend riding her bike during the day? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Algebra, STD2 A2 2009 HSC 13 MC
The volume of water in a tank changes over six months, as shown in the graph.
Consider the overall decrease in the volume of water.
What is the average percentage decrease in the volume of water per month over this time, to the nearest percent?
- 6%
- 11%
- 32%
- 64%