smc-970-10-Area

Calculus, 2ADV C3 2025 HSC 26

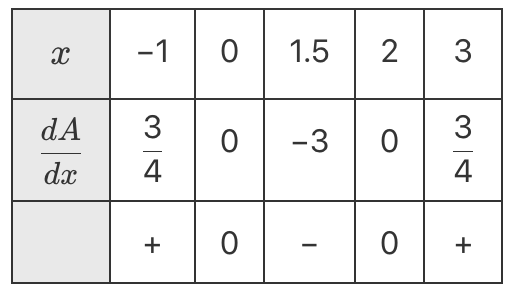
A piece of wire is 100 cm long. Some of the wire is to be used to make a circle of radius \(r\) cm. The remainder of the wire is used to make an equilateral triangle of side length \(x\) cm.

Show that the combined area of the circle and equilateral triangle is given by
\(A(x)=\dfrac{1}{4}\left(\sqrt{3} x^2+\dfrac{(100-3 x)^2}{\pi}\right)\). (2 marks)

--- 10 WORK AREA LINES (style=lined) ---
By considering the quadratic function in part (a), show that the maximum value of \(A(x)\) occurs when all the wire is used for the circle. (3 marks)
--- 15 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\text{See Worked Solutions}\)

b. \(\text{See Worked Solutions}\)

Show Worked Solution

a. \(\text{Area of equilateral triangle:}\)

\(A_{\Delta}=\dfrac{1}{2} a b\, \sin C=\dfrac{1}{2} \times x^2 \times \sin 60^{\circ}=\dfrac{\sqrt{3} x^2}{4}\)

\(\text{Wire remaining to make circle}=100-3 x\)

\(\text {Find radius of circle:}\)

\(2 \pi r=100-3 x \ \Rightarrow \ r=\dfrac{100-3 x}{2 \pi}\)

\(\text{Area of circle: }\)

\(A_{\text {circ }}=\pi r^2=\pi \times\left(\dfrac{100-3 x}{2 \pi}\right)^2=\dfrac{(100-3 x)^2}{4 \pi}\)

\(\text{Total Area}\)	\(=\dfrac{\sqrt{3} x^2}{4}+\dfrac{(100-3 x)^2}{4 \pi}\)
	\(=\dfrac{1}{4}\left(\sqrt{3} x^2+\dfrac{(100-3 x)^2}{\pi}\right)\)

b. \(\text{Note strategy clue in question: “By considering the quadratic..”}\)

\(\text {Expanding} \ A(x):\)

\(A(x)\)	\(=\dfrac{1}{4}\left(\sqrt{3} x^2+\dfrac{10\,000}{\pi}-\dfrac{600 x}{\pi}+\dfrac{9 x^2}{\pi}\right)\)
	\(=\dfrac{1}{4}\left(\sqrt{3}+\dfrac{9}{\pi}\right) x^2-\dfrac{150}{\pi} x+\dfrac{2500}{\pi}\)

\(\text{Consider limits on} \ x:\)

\(3 x \leqslant 100 \ \Rightarrow \ x \in\left[0,33 \frac{1}{3}\right]\)

\(\text{Consider vertex of concave up parabola}\ A(x):\)

\(x=-\dfrac{b}{2 a}=\dfrac{150}{\pi} \ ÷ \ \dfrac{1}{2}\left(\sqrt{3}+\dfrac{9}{\pi}\right) \approx 20.8\)

\(\text{By symmetry of the quadratic for} \ x \in\left[0,33 \dfrac{1}{3}\right],\)

\(A(x)_{\text{max}} \ \text{occurs at} \ \ x=0.\)

\(\text{i.e. when the wire is all used in the circle.}\)

Calculus, 2ADV C3 2024 MET2 18*

A trapezium has the following dimensions.

Show that the total area of the trapezium is given by
\(A=2x\sqrt{100-x^2}\) (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Find the value of \(x\) which maximises the area of the trapezium below. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

i. \(\text{See worked solutions}\)

ii. \(x=5\sqrt{2}\)

Show Worked Solution

i. \(A=\dfrac{h}{2}(a+b)\)

\(\text{By Pythagoras:}\ \ h=\sqrt{100-x^2}\)

\(A=\dfrac{\sqrt{100-x^2}}{2} \times (x + 3x) = 2x\sqrt{100-x^2}\)

ii.	\(\dfrac{dA}{dx}\)	\(=2\sqrt{(100-x^2}-\dfrac{2x^2}{\sqrt{100-x^2}}\)
		\(=\dfrac{2(100-x^2)-2x^2}{\sqrt{100-x^2}}\)
		\(=\dfrac{4(50-x^2)}{\sqrt{100-x^2}}\)

\(\text{Max/Min occurs when}\ \dfrac{dA}{dx}=0:\)

\(\dfrac{4(50-x^2)}{\sqrt{100-x^2}}\)	\(=0\quad(x \neq 10)\)
\(50-x^2\)	\(=0\)
(\(\sqrt{50}-x)(\sqrt{50}+x)\)	\(=0\)
\(\therefore\ x\)	\(=\sqrt{50}=5\sqrt{2}\quad (0<x<10)\)

\(\text{Check gradient for max using table:}\)

\(x\)	\(7\)	\(\sqrt{50}\)	\(7.2\)
\(A^{\prime}\)	\(0.56\)	\(0\)	\(-1.06\)
\(\text{Gradient}\)	\(+\)	\(0\)	\(-\)

\(\therefore\ x=5\sqrt{2}\ \text{maximises the area}\)

Two circles have the same centre \(O\). The smaller circle has radius 1 cm, while the larger circle has radius \((1 + x)\) cm. The circles enclose a region \(QRST\), which is subtended by an angle \(\theta\) at \(O\), as shaded.

The area of \(QRST\) is \(A\) cm\(^{2}\), where \(A\) is a constant and \(A \gt 0\).

Let \(P\) cm be the perimeter of \(QRST\).

By finding expressions for the area and perimeter of \(QRST\), show that \(P(x)=2x+\dfrac{2A}{x}\). (3 marks)
--- 10 WORK AREA LINES (style=lined) ---
Show that if the perimeter, \(P(x)\), is minimised, then \(\theta\) must be less than 2. (3 marks)
--- 14 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\text{Area}\ =\ \text{Sector}\ OQR-\text{Sector}\ OTS\)

\(A\)	\(=\dfrac{\theta}{2\pi} \times \pi (1+x)^2-\dfrac{\theta}{2\pi} \times \pi \times 1^2\)
\(A\)	\(=\dfrac{\theta}{2} (1+x)^2-\dfrac{\theta}{2}\)
\(A\)	\(=\dfrac{\theta}{2}(1+2x+x^2-1)\)
\(A\)	\(=\dfrac{\theta}{2}x(x+2)\)
\(\theta\)	\(=\dfrac{2A}{x(x+2)}\)

\(\text{Perimeter}\ QRST\)	\(=\dfrac{\theta}{2\pi} \times 2\pi(x+1)+\dfrac{\theta}{2\pi} \times 2\pi (1)+2x \)
	\(=\theta(x+1)+\theta+2x\)
	\(=\theta(x+2)+2x\)
	\(=\dfrac{2A}{x(x+2)}(x+2)+2x\)
	\(=2x+\dfrac{2A}{x}\)

b. \(P(x)=2x+\dfrac{2A}{x}\)

\(P^{′}(x) = 2-\dfrac{2A}{x^2}\)

\(P^{″}(x) = \dfrac{4A}{x^3} \gt0\ \ (x,A \gt 0)\)

\(\Rightarrow\ \text{MIN when}\ \ P^{′}(x)=0:\)

\(2-\dfrac{2A}{x^2}\)	\(=0\)
\(2x^2\)	\(=2A\)
\(x^2\)	\(=A\)

\(\text{Using part (a):}\)

\(\theta\)	\(=\dfrac{2A}{x(x-2)}\)
	\(=\dfrac{2x^2}{x(x+2)}\)
	\(=\dfrac{2x}{x+2}\)
	\(=2 \times \dfrac{x}{x+2} \)
	\( \lt 2\ \ \Big(\text{since}\ \ \dfrac{x}{x+2} \lt 1 \ \ \text{for all}\ x \Big) \)

\(\therefore\ \text{If}\ P(x)\ \text{is minimised,}\ \theta \lt 2. \)

Show Worked Solution

a. \(\text{Area}\ =\ \text{Sector}\ OQR-\text{Sector}\ OTS\)

\(A\)	\(=\dfrac{\theta}{2\pi} \times \pi (1+x)^2-\dfrac{\theta}{2\pi} \times \pi \times 1^2\)
\(A\)	\(=\dfrac{\theta}{2} (1+x)^2-\dfrac{\theta}{2}\)
\(A\)	\(=\dfrac{\theta}{2}(1+2x+x^2-1)\)
\(A\)	\(=\dfrac{\theta}{2}x(x+2)\)
\(\theta\)	\(=\dfrac{2A}{x(x+2)}\)

\(\text{Perimeter}\ QRST\)	\(=\dfrac{\theta}{2\pi} \times 2\pi(x+1)+\dfrac{\theta}{2\pi} \times 2\pi (1)+2x \)
	\(=\theta(x+1)+\theta+2x\)
	\(=\theta(x+2)+2x\)
	\(=\dfrac{2A}{x(x+2)}(x+2)+2x\)
	\(=2x+\dfrac{2A}{x}\)

♦ Mean mark (a) 41%.
COMMENT: Sector/arc calculations used in solution are for those who don’t want to remember formulas.

b. \(P(x)=2x+\dfrac{2A}{x}\)

\(P^{′}(x) = 2-\dfrac{2A}{x^2}\)

\(P^{″}(x) = \dfrac{4A}{x^3} \gt0\ \ (x,A \gt 0)\)

\(\Rightarrow\ \text{MIN when}\ \ P^{′}(x)=0:\)

\(2-\dfrac{2A}{x^2}\)	\(=0\)
\(2x^2\)	\(=2A\)
\(x^2\)	\(=A\)

\(\text{Using part (a):}\)

\(\theta\)	\(=\dfrac{2A}{x(x-2)}\)
	\(=\dfrac{2x^2}{x(x+2)}\)
	\(=\dfrac{2x}{x+2}\)
	\(=2 \times \dfrac{x}{x+2} \)
	\( \lt 2\ \ \Big(\text{since}\ \ \dfrac{x}{x+2} \lt 1 \ \ \text{for all}\ x \Big) \)

\(\therefore\ \text{If}\ P(x)\ \text{is minimised,}\ \theta \lt 2. \)

♦♦♦ Mean mark (b) 12%.

Calculus, 2ADV C3 2023 HSC 24

A gardener wants to build a rectangular garden of area 50 m² against an existing wall as shown in the diagram. A concrete path of width 1 metre is to be built around the other three sides of the garden.

Let \(x\) and \(y\) be the dimensions, in metres, of the outer rectangle as shown.

Show that \(y\) = \(\dfrac {50}{x - 2}+1 \). (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the value of \(x\) such that the area of the concrete path is a minimum. Show that your answer gives a minimum area. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

\(\text{See worked solutions}\)
\(x=12\)

Show Worked Solution

a.	\( (y-1)(x-2)\)	\(=50\)
	\(yx-2y-x+2\)	\(=50\)
	\(y(x-2)\)	\(=48+x\)
	\(y\)	\(=\dfrac{48+x}{x-2}\)
	\(y\)	\(=\dfrac{50+(x-2)}{x-2}\)
	\(y\)	\(=\dfrac{50}{x-2}+1\)

b. \(\text{Let}\ A=\ \text{area of concrete path}\)

\(A\)	\(= xy-50\)
	\(= x(\dfrac{50}{x-2}+1)-50\)
	\(=\dfrac{50x}{x-2}+x-50\)

\(\dfrac{dA}{dx}\)	\(=\dfrac{50(x-2)-50x}{(x-2)^2}+1\)
	\(=\dfrac{-100}{(x-2)^2}+1\)

\(\text{Max/min when}\ \dfrac{dA}{dx}=0\)

\(\dfrac{-100}{(x-2)^2}+1\)	\(=0\)
\((x-2)^2\)	\(=100\)
\(x-2\)	\(=\pm 10\)

\(x=12\ \ (x>0)\)

♦♦ Mean mark (b) 33%.

\(\text{Check gradients about}\ \ x=12: \)

\begin{array} {|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} x \rule[-1ex]{0pt}{0pt} & 10 & 12 & 14\\
\hline
\rule{0pt}{2.5ex}\dfrac{dA}{dx} \rule[-1ex]{0pt}{0pt} & – \frac{9}{16} & 0 & \frac{11}{36}\\
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \text{ \ } & \text{ _ } & \text{ / } \\
\hline
\end{array}

\(\therefore \text{Minimum at}\ x=12.\)

Calculus, 2ADV C3 2022 HSC 31

A line passes through the point `P(1,2)` and meets the axes at `X(x, 0)` and `Y(0, y)`, where `x>1`.

Show that `y=(2x)/(x-1)`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Find the minimum value of the area of triangle `XOY`. (4 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`4\ text{u}^2`

Show Worked Solution

a. `text{Show}\ \ y=(2x)/(x-1)`

`text{S}text{ince}\ \ m_(YP)=m_(PX):`

`(y-2)/(0-1)`	`=(2-0)/(1-x)`
`y-2`	`=(-2)/(1-x)`
`y`	`=2-2/(1-x)`
	`=(2(1-x)-2)/(1-x)`
	`=(-2x)/(1-x)`
	`=(2x)/(x-1)\ \ text{… as required}`

♦♦♦ Mean mark part (a) 17%.
COMMENT: `y=(2x)/(x-1)` is the expression of a relationship between the intercepts and not the equation of the line.

b.	`A`	`=1/2 xx b xxh`
		`=1/2x((2x)/(x-1))`
		`=(x^2)/(x-1)`

`(dA)/dx`	`=((x-1)*2x-x^2(1))/((x-1)^2)`
	`=(2x^2-2x-x^2)/((x-1)^2)`
	`=(x(x-2))/((x-1)^2)`

`text{SP’s occur when}\ \ (dA)/dx=0:`

`x=0\ \ text{or}\ \ 2`

`text{Use 1st derivative test to find max/min:}`

`=>\ text{MIN at}\ \ x=2`

`:.A_min`	`=1/2 xx 2 xx (2xx2)/(2-1)`
	`=4\ text{u}^2`

♦♦ Mean mark part (b) 29%.

Calculus, 2ADV C3 2020 HSC 25

A landscape gardener wants to build a garden in the shape of a rectangle attached to a quarter-circle. Let `x` and `y` be the dimensions of the rectangle in metres, as shown in the diagram.

The garden bed is required to have an area of 36 m² and to have a perimeter which is as small as possible. Let `P` metres be the perimeter of the garden bed.

Show that `P = 2x + 72/x`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the smallest possible perimeter of the garden bed, showing why this is the minimum perimeter. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solutions)`
`24\ text(m)`

Show Worked Solution

a.	`text(Area)`	`= xy + 1/4 pir^2`
	`36`	`= xy + 1/4 pix^2`
	`xy`	`= 36 – (pix^2)/4`
	`y`	`= 36/x – (pix)/4`

♦ Mean mark part (a) 47%.

`:. P`	`= 2x + 2y + 1/4(2pix)`
	`= 2x + 2(36/x – (pix)/4) + (pix)/2`
	`= 2x + 72/x – (pix)/2 + (pix)/2`
	`= 2x + 72/x`

b. `P = 2x + 72/x`

`(dP)/(dx)`	`= 2 – 72x^(−2)`
`(d^2P)/(dx^2)`	`= 144x^(−3)`

`text(Max or min when)\ \ (dP)/(dx) = 0:`

`2 – 72/(x^2)`	`= 0`
`2x^2`	`= 72`
`x^2`	`= 36`
`x`	`= 6,\ \ (x > 0)`

`text(When)\ \ x = 6,`

`(d^2P)/(dx^2) = 144/(6^3) = 2/3 > 0`

`=>\ text(MIN at)\ x = 6`

`:. P_text(min)`	`= 2 xx 6 + 72/6`
	`= 24\ text(m)`

Calculus, 2ADV C4 2019 HSC 16c

The diagram shows the region `R`, bounded by the curve `y = x^r`, where `r >= 1`, the `x`-axis and the tangent to the curve at the point `(1, 1)`.

Show that the tangent to the curve at `(1, 1)` meets the `x`-axis at

`qquad ((r - 1)/r, 0)`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Using the result of part (i), or otherwise, show that the area of the region `R` is

`qquad (r - 1)/(2r (r + 1))`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the exact value of `r` for which the area of `R` is a maximum. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ text{(See Worked Solutions)}`
`text(Proof)\ text{(See Worked Solutions)}`
`r = 1 + sqrt 2`

Show Worked Solution

i.	`y`	`= x^r`
	`(dy)/(dx)`	`= r x^(r – 1)`

`text(When)\ \ x = 1, \ (dy)/(dx) = r`

♦♦ Mean mark part (i) 31%.

`text(Equation of tangent:)`

`y – 1`	`= r(x – 1)`
`y`	`= rx – r + 1`

`text(When)\ \ y = 0:`

`rx – r + 1`	`= 0`
`rx`	`= r – 1`
`x`	`= (r – 1)/r`

`:.\ text(T)text(angent meets)\ x text(-axis at)\ \ ((r – 1)/r, 0)`

ii. `text(Area under curve)`

♦♦♦ Mean mark part (ii) 21%.

`= int_0^1 x^r`

`= [1/(r + 1) ⋅ x^(r + 1)]_0^1`

`= 1/(r + 1) xx 1^(r + 1) – 0`

`= 1/(r + 1)`

`text(Area under tangent)`

`= 1/2 xx b xx h`

`= 1/2 (1 – (r – 1)/r) xx 1`

`= 1/2 (1 – (r – 1)/r)`

`:. R`	`= 1/(r + 1) – 1/2(1 – (r – 1)/r)“
	`= 1/(r + 1) – 1/(2r) [r – (r – 1)]`
	`= 1/(r + 1) – 1/(2r)`
	`= (2r – (r + 1))/(2r(r + 1))`
	`= (r – 1)/(2r(r + 1))`

iii.	`R`	`= (r – 1)/(2r(r + 1)) = (r – 1)/(2r^2 + 2r)`
	`(dR)/(dr)`	`= ((2r^2 + 2r) xx 1 – (r – 1)(4r + 2))/(2r^2 + 2r)^2`
		`= (2r^2 + 2r – 4r^2 – 2r + 4r + 2)/(2r^2 + 2r)^2`
		`= (-2r^2 + 4r + 2)/(2r^2 + 2r)^2`
		`= (-2(r^2 – 2r – 1))/(2r^2 + 2r)^2`

`text(Find)\ \ r\ \ text(when)\ \ (dR)/(dr) = 0:`

♦♦ Mean mark part (iii) 23%.

`r^2 – 2r – 1 = 0`

`r`	`= (2 +- sqrt((-2)^2 – 4 xx 1 xx (-1)))/2 `
	`= (2 +- sqrt 8)/2`
	`= 1 + sqrt 2\ \ (r >= 1)`

	`qquadr qquad`	`qquad 1 qquad`	`\ \ 1 + sqrt 2\ \ `	`qquad 3 qquad`
	`(dR)/(dr)`	`1/4`	`0`	`-1/144`

`:. R_text(max)\ text(occurs when)\ \ r = 1 + sqrt 2`

Calculus, 2ADV C4 SM-Bank 12

Let `f(x) = 2e^(-x/5)\ \ \ text(for)\ \ x>=0`

A right-angled triangle `OQP` has vertex `O` at the origin, vertex `Q` on the `x`-axis and vertex `P` on the graph of `f`, as shown. The coordinates of `P` are `(x, f(x)).`

Find the area, `A`, of the triangle `OPQ` in terms of `x`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the maximum area of triangle `OQP` and the value of `x` for which the maximum occurs. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Let `S` be the point on the graph of `f` on the `y`-axis and let `T` be the point on the graph of `f` with the `y`-coordinate `1/2`.Find the area of the region bounded by the graph of `f` and the line segment `ST`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`x e^(-x/5)`
`5/e\ text(u²)`
`25/4 log_e (4) – 15/2\ text(u²)`

Show Worked Solution

i.	`text(Area)`	`= 1/2 xx b xx h`
		`= 1/2x(2e^(-x/5))`
	`:. A`	`= xe^(-x/5)`

ii. `text(Stationary point when)\ \ (dA)/(dx) = 0,`

♦ Mean mark (Vic) 35%.

`x(-1/5 e^(-x/5)) + e^(-x/5)`	`= 0`
`e^(-x/5)(1 – x/5)`	`= 0`
`:. x`	`= 5\ \ \ \ (e^(-x/5) >0,\ \ text(for all)\ x)`

`text(When)\ \ x = 5,\ \ A`	`= xe^(-x/5)= 5e^-1`

`:. A_max = 5/e\ text(u², when)\ \ x = 5`

iii. `text(Find)\ \ S:\ F(0) = 2`

`=>S(0, 2)`

♦♦ Mean mark (Vic) 32%.

`text(Find)\ \ T:\ \ \ `	`2e^(-x/5)`	`= 1/2`
	`e^(-x/5)`	`= 1/4`
	`-x/5`	`= log_e (1/4)`
	`x`	`= 5 log_e (4)`

`=> T(5log_e(4), 1/2)`

`:.\ text(Area)`	`= text(Area)\ SOAT – int_0^(5 log_e(4)) (2e^(-x/5)) dx`
	`=1/2h(a+b) + 10 [e^(-x/5)]_0^(5 log_e (4))`
	`= 5/2 log_e (4) (2 + 1/2) + 10 [e^(-log_e (4)) – e^0]`
	`= 25/4 log_e (4) +10 (1/4 – 1)`
	`= 25/4 log_e (4) – 15/2\ text(u²)`

Calculus, 2ADV C3 2016 HSC 14c

A farmer wishes to make a rectangular enclosure of area 720 m². She uses an existing straight boundary as one side of the enclosure. She uses wire fencing for the remaining three sides and also to divide the enclosure into four equal rectangular areas of width `x` m as shown.

Show that the total length, `l` m, of the wire fencing is given by

`l = 5x + 720/x`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the minimum length of wire fencing required, showing why this is the minimum length. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`120\ text(m)`

Show Worked Solution

i.	`text(Area)`	`= xy`
	`720`	`= xy`
	`y`	`= 720/x`

`l`	`= 5x + y`
	`= 5x + 720/x\ \ text(… as required)`

ii.	`(dl)/(dx)`	`= 5 – 720/x^2`
	`(d^2l)/(dx^2)`	`= 1440/x^3`

`text(Max/Min when)\ \ (dl)/(dx) = 0,`

`5`	`= 720/x^2`
`x^2`	`= 144`
`x`	`= 12,\ \ x > 0`

`text(When)\ \ x = 12,\ \ (d^2l)/(dx^2) > 0`

`:.\ text(Minimum occurs when)\ \ x = 12`

`:.\ text(Minimum fencing)`

`= 5 xx 12 + 720/12`

`= 120\ text(m)`

Calculus, 2ADV C3 2004 HSC 10b

The diagram shows a triangular piece of land `ABC` with dimensions `AB = c` metres, `AC = b` metres and `BC = a` metres, where `a ≤ b ≤ c`.

The owner of the land wants to build a straight fence to divide the land into two pieces of equal area. Let `S` and `T` be points on `AB` and `AC` respectively so that `ST` divides the land into two pieces of equal area.

Let `AS = x` metres, `AT = y` metres and `ST = z` metres.

Show that `xy = 1/2 bc`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Use the cosine rule in triangle `AST` to show that

`z^2 = x^2 + (b^2c^2)/(4x^2) − bc cos A.` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Show that the value of `z^2` in the equation in part (ii) is a minimum when

`x = sqrt((bc)/2)`. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---
Show that the minimum length of the fence is `sqrt(((P − 2b)(P − 2c))/2)` metres, where `P = a + b + c`.

(You may assume that the value of `x` given in part (iii) is feasible.) (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

i.	`text(Area)\ \ ΔABC`	`= 1/2\ bc sin A`
	`text(Area)\ \ ΔAST`	`= 1/2\ xy sin A`

`text(Area)\ \ ΔAST`	`= 1/2 xx text(Area)\ \ ΔABC\ \ \ text{(given)}`
`1/2\ xy sin A`	`= 1/2 xx 1/2\ bc sin A`
`xy sin A`	`= 1/2\ bc sin A`
`:. xy`	`= 1/2\ bc\ \ …\ text(as required.)`

ii. `text(Using the cosine rule in)\ \ ΔAST,`

`z^2 = x^2 + y^2 − 2xy cos A`

`text(S)text(ince)\ \ xy`	`= 1/2\ bc`
`:. y`	`= (bc)/(2x)`

`:. z^2`	`= x^2 + ((bc)/(2x))^2 − 2x((bc)/(2x)) cos A`
	`= x^2 + (b^2c^2)/(4x^2) − bc cos A`

iii.	`z^2`	`= x^2 + ((b^2c^2)/4)x^(−2) − bc cos A`
	`(d(z^2))/(dx)`	`= 2x − (2b^2c^2)/4 x^(−3)= 2x − (b^2c^2)/(2x^3)`
	`(d^2(z^2))/(dx^2)`	`= 2 + (3b^2c^2)/2 x^(−4)= 2 + (3b^2c^2)/(2x^4)`

`text(SP’s occur when)\ \ (d(z^2))/(dx)=0`

`2x − (b^2c^2)/(2x^3)`	`= 0`
`4x^4 − b^2c^2`	`= 0`
`4x^4`	`= b^2c^2`
`x^4`	`= (b^2c^2)/4`
`x^2`	`= (bc)/2`
`x`	`= sqrt((bc)/2),\ \ \ (x > 0)`

` (d^2(z^2))/(dx^2)=2 + (3b^2c^2)/(2x^4)>0\ \ \ text{(for all}\ xtext{)}`

`:.\ text(A minimum value of)\ z^2\ text(when)\ x = sqrt((bc)/2).`

iv. `cos A = (b^2 + c^2 − a^2)/(2bc)`

`text(When)\ \ x = sqrt((bc)/2),`

`:. z^2`	`= x^2 + (b^2c^2)/(4x^2) − bc cos A`
	`= (bc)/2 + (b^2c^2)/(4((bc)/2)) − bc((b^2 + c^2 − a^2)/(2bc))`
	`= (bc)/2 + (bc)/2 − ((b^2 + c^2 − a^2)/2)`
	`= (2bc – b^2 − c^2 +a^2)/2`
	`= (a^2 − (b^2 − 2bc + c^2))/2`
	`= 1/2[a^2 − (b − c)^2]`
	`= 1/2[(a − (b − c))(a + (b − c))]`
	`= 1/2[(a − b + c)(a + b − c)]`
	` = 1/2[(a + b + c − 2b)(a + b + c − 2c)]`
	`= ((P − 2b)(P − 2c))/2\ \ \ text{(using}\ \ P = a + b + c text{)}`

`:.z = sqrt(((P − 2b)(P − 2c))/2)\ \ text(metres)\ \ …\ text(as required.)`

Calculus, 2ADV C3 2014 HSC 16c

The diagram shows a window consisting of two sections. The top section is a semicircle of diameter `x` m. The bottom section is a rectangle of width `x` m and height `y` m.

The entire frame of the window, including the piece that separates the two sections, is made using 10 m of thin metal.

The semicircular section is made of coloured glass and the rectangular section is made of clear glass.

Under test conditions the amount of light coming through one square metre of the coloured glass is 1 unit and the amount of light coming through one square metre of the clear glass is 3 units.

The total amount of light coming through the window under test conditions is `L` units.

Show that `y = 5 - x(1 + pi/4)`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Show that `L = 15x - x^2 (3 + (5pi)/8)`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the values of `x` and `y` that maximise the amount of light coming through the window under test conditions. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`x = 1.511\ text(m and)\ \ y = 2.302\ text(m)`

Show Worked Solution

`text(Frame is 10m)`

`10`	`= 2x + 2y + 1/2 pi x`
`2y`	`= 10\ – 2x\ – 1/2 pi x`
`:.y`	`= 5\ – x\ – pi/4 x`
	`= 5\ – x (1 + pi/4)\ \ \ text(… as required.)`

♦ Mean mark 35%

ii.	`text(Area)\ text{(clear)}`	`= x xx y`
	`text(Area)\ text{(colour)}`	`= 1/2 xx pi r^2`
		`= 1/2 xx pi (x/2)^2`
		`= (pi x^2)/8`

`:.\ L`	`= 3xy + ((pix^2)/8 xx 1)`
	`= 3x [5\ – x (1 + pi/4)] + (pix^2)/8\ \ \ text{(see part (i))}`
	`= 15x\ – 3x^2\ – (3x^2pi)/4 + (x^2 pi)/8`
	`= 15x\ – 3x^2\ – (5x^2 pi)/8`
	`= 15x\ – x^2 (3 + (5pi)/8)\ \ \ text(… as required)`

♦ Mean mark 38%
COMMENT: A sanity check for your answer could be to compare your answers to the perimeter restriction of 10m.

iii.	`L`	`= 15x\ – x^2 (3 + (5pi)/8)`
	`(dL)/(dx)`	`= 15\ – 2x (3 + (5pi)/8)`
	`(d^2L)/(dx^2)`	`= -2 (3 + (5pi)/8)`

`text(Max or min when)\ (dL)/(dx) = 0`

`15\ – 2x (3x + (5pi)/8)=`	`0`
`2x (3 + (5pi)/8)=`	`15`
`x=`	`15/(2 (3 + (5pi)/8)`
`=`	`1.51103…`
`=`	`1.511\ \ \ text{(3 d.p.)}`

`text(S)text(ince)\ (d^2L)/(dx^2) < 0\ \ \ => text(MAX)`

`text(When)\ \ x`	`= 1.511`
`y`	`= 5\ – 1.511 (1 + pi/4)`
	`= 2.3022…`
	`= 2.302\ text{(3 d.p.)}`

`:.\ text(MAX light when)\ x = 1.511\ text(m)`

`text(and)\ y = 2.302\ text(m.)`

Calculus, 2ADV C3 2008 HSC 10b

The diagram shows two parallel brick walls `KJ` and `MN` joined by a fence from `J` to `M`. The wall `KJ` is `s` metres long and `/_KJM=alpha`. The fence `JM` is `l` metres long.

A new fence is to be built from `K` to a point `P` somewhere on `MN`. The new fence `KP` will cross the original fence `JM` at `O`.

Let `OJ=x` metres, where `0<x<l`.

Show that the total area, `A` square metres, enclosed by `DeltaOKJ` and `DeltaOMP` is given by

`A=s(x-l+l^2/(2x))sin alpha`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the value of `x` that makes `A` as small as possible. Justify the fact that this value of `x` gives the minimum value for `A`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Hence, find the length of `MP` when `A` is as small as possible. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`l/sqrt2`
`(sqrt2-1)s\ \ text(metres)`

Show Worked Solution

`A=text(Area)\ Delta OJK+text(Area)\ Delta OMP`

♦♦♦ Low mean marks highlighted (although exact data not available before 2009).

`text(Using sine rule)`

`text(Area)\ Delta OJK=1/2\ x s sin alpha`

`text(Area)\ DeltaOMP =>text(Need to find)\ \ MP`

`/_OKJ`	`=/_MPO\ \ text{(alternate angles,}\ MP\ text(\|\|)\ KJtext{)}`
`/_PMO`	`=/_OJK=alpha\ \ text{(alternate angles,}\ MP\ text(\|\|)\ KJtext{)}`

`:.\ DeltaOJK\ text(|||)\ Delta OMP\ \ text{(equiangular)}`

`=>x/s`	`=(l-x)/(MP)\ `	` text{(corresponding sides of similar triangles)}`
`MP`	`=(l-x)/x *s`

`text(Area)\ Delta\ OMP`	`=1/2 (l-x)* MP * sin alpha`
	`=1/2 (l-x)((l-x))/x s sin alpha`

`:. A`	`=1/2 xs sin alpha+1/2 (l-x)((l-x))/x* s sin alpha`
	`=s sin alpha(1/2 x+1/2 (l-x)*((l-x))/x)`
	`=s sin alpha(1/2 x+(l-x)^2/(2x))`
	`=s sin alpha(1/2 x+l^2/(2x)-l+1/2 x)`
	`=s(x-l+l^2/(2x))sin alpha\ \ \ \ text(… as required)`

ii. `text(Find)\ x\ text(such that)\ A\ text(is a minimum)`

MARKER’S COMMENT: Students who could not complete part (i) are reminded that they can still proceed to part (ii) and attempt to differentiate the result given.
Note that `l` and `alpha` are constants when differentiating.

`A`	`=s(x-l+l^2/(2x))sin alpha`
`(dA)/(dx)`	`=s(1-l^2/(2x^2))sin alpha`

`text(MAX/MIN when)\ (dA)/(dx)=0`

`s(1-l^2/(2x^2))sin alpha`	`=0`
`l^2/(2x^2)`	`=1`
`2x^2`	`=l^2`
`x^2`	`=l^2/2`
`x`	`=l/sqrt2,\ \ \ x>0`

`(d^2A)/(dx^2)=s((l^2)/(2x^3))sin alpha`

`text(S)text(ince)\ \ 0<alpha<90°\ \ =>\ sin alpha>0,\ \ l>0\ \ text(and)\ \ x>0`

`(d^2A)/(dx^2)>0\ \ \ =>text(MIN at)\ \ x=l/sqrt2`

iii. `text(S)text(ince)\ \ MP=((l-x))/x s\ \ text(and MIN when)\ \ x=l/sqrt2`

`MP`	`=((l-l/sqrt2)/(l/sqrt2))s xx sqrt2/sqrt2`
	`=((sqrt2 l-l))/l s`
	`=(sqrt2-1)s\ \ text(metres)`

`:.\ MP=(sqrt2-1)s\ \ text(metres when)\ A\ text(is a MIN.)`

Calculus, 2ADV C3 2011 HSC 10b

A farmer is fencing a paddock using `P` metres of fencing. The paddock is to be in the shape of a sector of a circle with radius `r` and sector angle `theta` in radians, as shown in the diagram.

Show that the length of fencing required to fence the perimeter of the paddock is

`P=r(theta+2)`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Show that the area of the sector is `A=1/2 Pr-r^2`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the radius of the sector, in terms of `P`, that will maximise the area of the paddock. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the angle `theta` that gives the maximum area of the paddock. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Explain why it is only possible to construct a paddock in the shape of a sector if

`P/(2(pi+1)) <\ r\ <P/2` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`text{Proof (See Worked Solutions)}`
`r=P/4`
`2\ text(radians)`
`text{Proof (See Worked Solutions)}`

Show Worked Solution

i. `text(Need to show)\ \ P=r(theta+2)`

`P`	`=(2xxr)+theta/(2pi)xx2pir`
	`=2r+ r theta`
	`=r(theta+2)\ \ text(… as required)`

ii. `text(Need to show)\ \ A=1/2 Pr-r^2`.

`text(S)text(ince)\ \ P=r(theta+2)\ \ \ =>\ theta=(P-2r)/r`

♦ Mean mark 41%.
TIP: Area of a sector `=pi r^2 xx` the percentage of the circle that the sector angle accounts for, i.e. `theta/(2 pi)` radians. `:. A=pi r^2“ xx theta/(2 pi)=1/2 r^2 theta`.

`:. A`	`=1/2 r^2 theta`
	`=1/2 r^2*(P-2r)/r`
	`=1/2(Pr-2r^2)`
	`=1/2 Pr-r^2\ \ text(… as required)`

iii. `A=1/2 Pr-r^2`

♦♦ Mean mark 29%
MARKER’S COMMENT: The second derivative test proved much more successful and easily proven in this part. Make sure you are comfortable choosing between it and the 1st derivative test depending on the required calcs.

`(dA)/(dr)=1/2 P-2r`

`text(MAX or MIN when)\ \ (dA)/(dr)=0`

`1/2 P-2r`	`=0`
`2r`	`=1/2 P`
`r`	`=P/4`

`(d^2A)/(dr^2)=-2\ \ \ \ =>text(MAX)`

`:.\ text(Area is a MAX when)\ r=P/4\ text(units)`

iv. `text(Need to find)\ theta\ text(when area is a MAX)\ =>\ r=P/4`

♦♦♦ Mean mark 20%

`P`	`=r(theta+2)`
	`=P/4(theta+2)`
`4P`	`=P(theta+2)`
`theta+2`	`=4`
`theta`	`=2\ text(radians)`

v. `text(For a sector to exist)\ \ 0<\ theta\ <2pi, \ \ text(and)\ \ theta=(P-2r)/r`

♦♦♦ Mean mark 4%. A BEAST!
MARKER’S COMMENT: When asked to ‘explain’, students should support their answer with a mathematical argument.

`=>(P-2r)/r`	`>0`
`P-2r`	`>0`
`r`	`<P/2`

`=>(P-2r)/r`	`<2pi`
`P-2r`	`<2r pi`
`2r pi+2r`	`>P`
`2r(pi+1)`	`>P`
`r`	`>P/(2(pi+1))`

`:.P/(2(pi+1)) <\ r\ <P/2\ \ text(… as required)`

Calculus, 2ADV C3 2012 HSC 16b

The diagram shows a point `T` on the unit circle `x^2+y^2=1` at an angle `theta` from the positive `x`-axis, where `0<theta<pi/2`.

The tangent to the circle at `T` is perpendicular to `OT`, and intersects the `x`-axis at `P`, and the line `y=1` intersects the `y`-axis at `B`.

Show that the equation of the line `PT` is `xcostheta+ysin theta=1`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Find the length of `BQ` in terms of `theta`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Show that the area, `A`, of the trapezium `OPQB` is given by

`A=(2-sintheta)/(2costheta)` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Find the angle `theta` that gives the minimum area of the trapezium. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`(1-sin theta)/cos theta`
`text{Proof (See Worked Solutions)}`
`theta=pi/6\ \ text(radians)`

Show Worked Solution

`text(Find)\ T:`

♦♦ Mean mark 20%

`text(S)text(ince)\ \ cos theta=x/1\ \ \ text(and)\ \ \ sin theta=y/1`

`:. T\ (cos theta, sin theta)`

`text(Gradient of)\ OT=sin theta/cos theta`

`:.\ text(Gradient)\ PT=-cos theta/sin theta\ \ text{(} _|_ text{lines)}`

`text(Equation of)\ PT\ text(where)`

`m=-cos theta/sin theta,\ \ text(and through)\ \ (cos theta, sin theta)`

`text(Using)\ \ y-y_1`	`=m(x-x_1)`
`y-sin theta`	`=-cos theta/sin theta(x-cos theta)`
`y sin theta-sin^2 theta`	`=-x cos theta+cos^2 theta`
`x cos theta+y sin theta`	`=sin^2 theta+cos^2 theta`
`x cos theta+y sin theta`	`=1\ \ \ \ \ text(… as required)`

ii. `text(Find)\ Q:`

`Q\ => text(intersection of)\ xcos theta+y sin theta=1\ \ text(and)\ \ y=1`

`x cos theta+sin theta`	`=1`
`x cos theta`	`=1-sin theta`
`x`	`=(1-sin theta)/cos theta`

`:.\ text(Length of)\ BQ\ text(is)\ \ (1-sin theta)/cos theta\ text(units)`

iii. `text(Show Area)\ OPQB=(2-sin theta)/(2cos theta)`

`A=1/2h(a+b)\ \ text(where)\ \ h=OB=1\ \ a=OP\ \ text(and)`

`b=BQ=(1-sin theta)/cos theta`

`text(Find length)\ OP:`

`P => xcos theta+ysin theta=1 \ text(cuts)\ \ x text(-axis)`

♦♦ Mean mark 24%

`xcos theta`	`=1`
`x`	`=1/cos theta`
`=>text(Length)\ OP`	`=1/cos theta`

`text(Area)\ OPQB`	`=1/2xx1(1/cos theta+(1-sin theta)/cos theta)`
	`=1/2((2-sin theta)/cos theta)`
	`=(2-sin theta)/(2cos theta)\ \ text(u²)\ \ \ text(… as required)`

iv. `text(Find)\ theta\ text(such that Area)\ OPQB\ text(is a MIN)`

`A`	`=(2-sin theta)/(2cos theta)`
`(dA)/(d theta)`	`=(2cos theta(-cos theta)-(2- sin theta)(-2 sin theta))/(4cos^2 theta)`
	`=(4 sin theta-2sin^2 theta-2 cos^2 theta)/(4 cos^2 theta)`
	`=(4sin theta-2(sin^2 theta+cos^2 theta))/(4 cos^2 theta)`
	`=(4sin theta-2)/(4cos^2 theta)`
	`=(2sin theta-1)/(2 cos^2 theta)`

Mean mark 19%
IMPORTANT: Look for any opportunity to use the identity `sin^2 theta“+cos^2 theta=1` → often a key to simplifying difficult trig equations.

`text(MAX or MIN when)\ (dA)/(d theta)=0`

`=>2sin theta-1`	`=0`
`sin theta`	`=1/2`
`theta`	`=pi/6\ \ \ \ \0<theta<pi/2`

`text(Test for MAX/MIN)`

IMPORTANT: Is the 1st or 2nd derivative test easier here? Examiners have often made one significantly easier than the other.

`text(If)\ theta=pi/12\ \ (dA)/(d theta)<0`

`text(If)\ theta=pi/3\ \ (dA)/(d theta)>0\ \ =>text(MIN)`

`:.\text(Area)\ OPQB\ text(is a MIN when)\ theta=pi/6`.