SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, 2ADV C3 2018 HSC 16a

A sector with radius 10 cm and angle  `theta`  is used to form the curved surface of a cone with base radius `x` cm, as shown in the diagram.
 


 

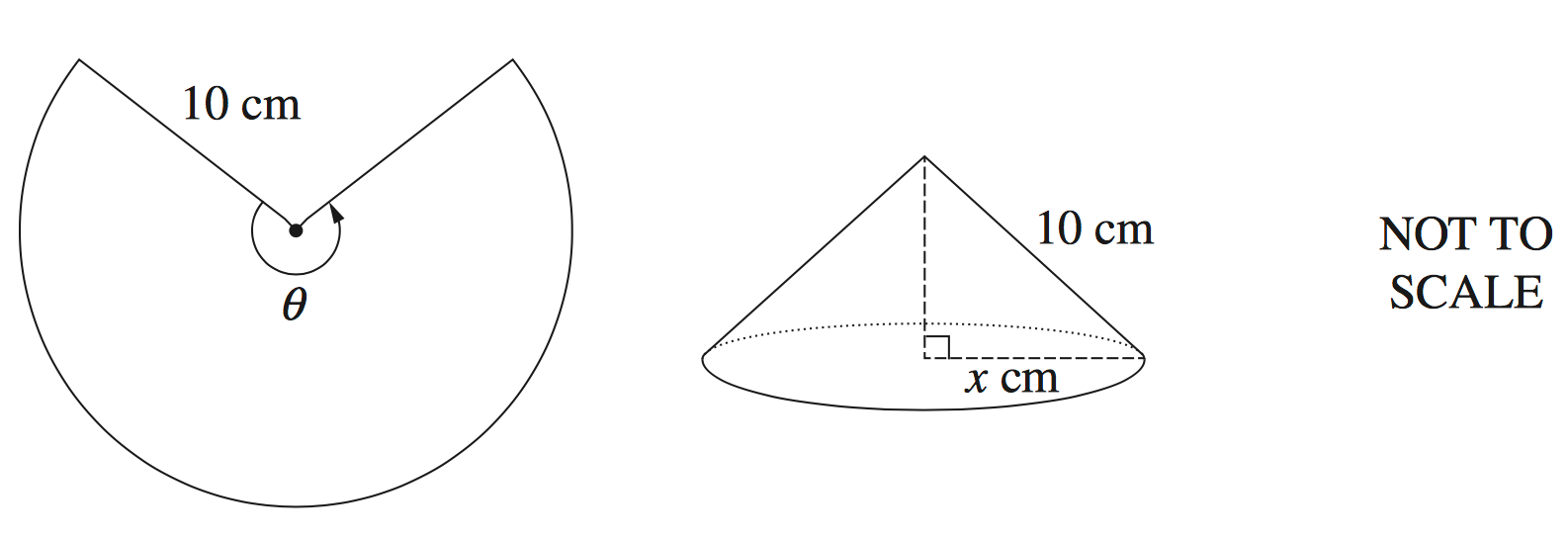
The volume of a cone of radius `r` and height `h` is given by  `V = 1/3 pi r^2 h`.

  1. Show that the volume, `V` cm³, of the cone described above is given by
     
          `V = 1/3 pi x^2 sqrt(100-x^2)`.   (1 mark)

  2. Show that  `(dV)/(dx) = (pi x (200-3x^2))/(3 sqrt(100-x^2))`.   (2 marks)

  3. Find the exact value of  `theta`  for which `V` is a maximum.   (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `(2 sqrt 2 pi)/sqrt 3`
Show Worked Solution

i.   `V = 1/3 pi r^2 h`

`text(Using Pythagoras,)`

`h = sqrt(100-x^2)`

`r = x`

`:.\ text(Volume) = 1/3 pi x^2 sqrt(100-x^2)`
 

♦ Mean mark (ii) 45%.

ii.   `V` `= 1/3 pi x^2 sqrt(100-x^2)`
  `(dV)/(dh)` `= 1/3 pi [2x ⋅ sqrt(100-x^2)-2x ⋅ 1/2 (100-x^2)^(-1/2) ⋅ x^2]`
    `= 1/3 pi [(2x (100-x^2)-x^3)/sqrt(100-x^2)]`
    `= 1/3 pi [(200 x-2x^3-x^3)/sqrt(100-x^2)]`
    `= (pi x(200-3x^2))/(3 sqrt (100-x^2))\ \ text{.. as required}`

 

iii.  `text(Find)\ \ x\ \ text(when)\ \ (dV)/(dx) = 0`

♦♦ Mean mark (iii) 23%.

`200-3x^2` `= 0`
`x` `= sqrt(200/3)`

 
`text(When)\ \ x < sqrt(200/3),\ (200-3x^2) > 0`

`=> (dV)/(dx) > 0`

`text(When)\ \ x > sqrt(200/3),\ (200-3x^2) < 0`

`=> (dV)/(dx) < 0`

`:.\ text(MAX when)\ \ x = sqrt(200/3)`
 

`text(Equating the arc length of the section)`

`text(to the circumference of the cone:)`

`2 pi r ⋅ theta/(2 pi)` `= 2 pi ⋅ x`
`10 theta` `= 2 pi sqrt (200/3)`
`:. theta` `= (2 pi ⋅ 10 sqrt 2)/(10 ⋅ sqrt 3)`
  `= (2 sqrt 2 pi)/sqrt 3`

Calculus, 2ADV C3 2015 HSC 16c

The diagram shows a cylinder of radius `x` and height `y` inscribed in a cone of radius `R` and height `H`, where `R` and `H` are constants.
  

The volume of a cone of radius `r` and height `h` is  `1/3 pi r^2 h.`

The volume of a cylinder of radius `r` and height `h` is  `pi r^2 h.`

  1. Show that the volume, `V`, of the cylinder can be written as
     
         `V = H/R pi x^2 (R-x).`   (3 marks)

  2. By considering the inscribed cylinder of maximum volume, show that the volume of any inscribed cylinder does not exceed `4/9` of the volume of the cone.   (4 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

i.   `text(Show)\ \ V = H/R pi x^2 (R-x)`
 

♦♦ Mean mark (i) 16%.

 

`text(Consider)\ \ Delta ABC and Delta DEC`

`/_ ABC = /_DEC = 90°`

`/_ BCA\ \ text(is common)`

`:. Delta ABC\ \ text(|||)\ \ Delta DEC\ \ text{(equiangular)}`

`:.\ (DE)/(EC)`

`= (AB)/(BC)`

`\ text{(corresponding sides of}`

`\ text{similar triangles)}`
`y/(R-x)` `= H/R`  
`y` `= H/R (R-x)`  

 

`text(Volume of cylinder)`

`= pi r^2 h`

`= pi x^2 xx H/R (R-x)`

`= H/R pi x^2 (R-x)\ \ text(…  as required.)`
 

♦♦ Mean mark (ii) 21%.

ii.   `V= H/R pi x^2 (R-x)`

`(dV)/(dx)` `= H/R pi [(x^2 xx -1) + 2x (R-x)]`
  `= H/R pi [-x^2 + 2xR-2x^2]`
  `= H/R pi [2xR-3x^2]`
`(dV^2)/(dx^2)` `= H/R pi [2R-6x]`

 

`text(Max or min when)\ \ (dV)/(dx) = 0`

`H/R pi [2xR-3x^2]` `= 0`
`2xR-3x^2` `= 0`
`x (2R-3x)` `= 0`
`x = 0\ \ or\ \ 3x` `= 2R`
`x` `= (2R)/3`

 

`text(When)\ \ x = 0:`

`(d^2V)/(dx^2) = H/R pi [2R-0] > 0\ \ =>\  text(MIN)`
 

`text(When)\ \ x = (2R)/3:`

`(d^2V)/(dx^2)` `= H/R pi [2R-6 xx (2R)/3]`
  `= H/R pi [-2R] < 0\ \ =>\ \text{MAX}`

 
`text(Maximum Volume of cylinder)`

`= H/R pi ((2R)/3)^2 (R-(2R)/3)`

`= H/R pi xx (4R^2)/9 xx R/3`

`= (4 pi H R^2)/27`

 

`text(Volume of cone)\ = 1/3 pi R^2 H`

`:.\ text(Max Volume of Cylinder)/text(Volume of cone)`

`= ((4 pi H R^2)/27)/(1/3 pi R^2 H)`

`= (4 pi H R^2)/27 xx 3/(pi R^2 H)`

`= 4/9`

 

`:.\ text(The volume of the inscribed cylinder does)`

`text(not exceed)\ 4/9\ text(of the cone volume.)`

Calculus, 2ADV C3 2006 HSC 9c

A cone is inscribed in a sphere of radius `a`, centred at `O`. The height of the cone is `x` and the radius of the base is `r`, as shown in the diagram.

  1. Show that the volume, `V`, of the cone is given by
     
         `V = 1/3 pi(2ax^2 - x^3)`.  (2 marks)

  2. Find the value of `x` for which the volume of the cone is a maximum. You must give reasons why your value of `x` gives the maximum volume.  (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `x = 4/3 a`
Show Worked Solution

i.  `text(Show)\ V = 1/3 pi (2ax^2 – x^3)`

`V = 1/3 pi r^2 h`

`text(Using Pythagoras)`

`(x – a)^2 + r^2` `= a^2`
`r^2` `= a^2 – (x – a)^2`
  `= a^2 – x^2 + 2ax – a^2`
  `= 2ax – x^2`
`:. V` `= 1/3 xx pi xx (2ax – x^2) xx x`
  `= 1/3 pi (2ax^2 – x^3)\ …\ text(as required)`

 

ii.  `(dV)/(dx) = 1/3 pi (4ax – 3x^2)`

`(d^2V)/(dx^2) = 1/3 pi (4a – 6x)`

`text(Max or min when)\ (dV)/(dx) = 0`

`1/3 pi (4ax – 3x^2)` `= 0`
`4ax – 3x^2` `= 0`
`x(4a – 3x)` `= 0`
`3x` `= 4a,` ` \ \ \ \ x ≠ 0`
`x` ` =4/3 a`  

 

`text(When)\ \ x = 4/3 a`

`(d^2V)/(dx^2)` `= 1/3 pi (4a – 6 xx 4/3 a)`
  `= 1/3 pi (-4a) < 0`
`=>\ text(MAX)`

 

`:.\ text(Cone volume is a maximum when)\ \ x = 4/3 a.`