smc-975-40-Exponential

Calculus, 2ADV C4 2023 HSC 32

The curves and intersect at exactly one point as shown in the diagram. The point of intersection has coordinates . (Do NOT prove this.)

Show that the area bounded by the two curves and the -axis, as shaded in the diagram, is . (3 marks)

--- 7 WORK AREA LINES (style=lined) ---
Find the values of such that the curves and intersect at two points. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

a.

♦♦♦ Mean mark (b) 14%.

Calculus, 2ADV C4 2021 HSC 28

The region bounded by the graph of the function and the coordinate axes is shown

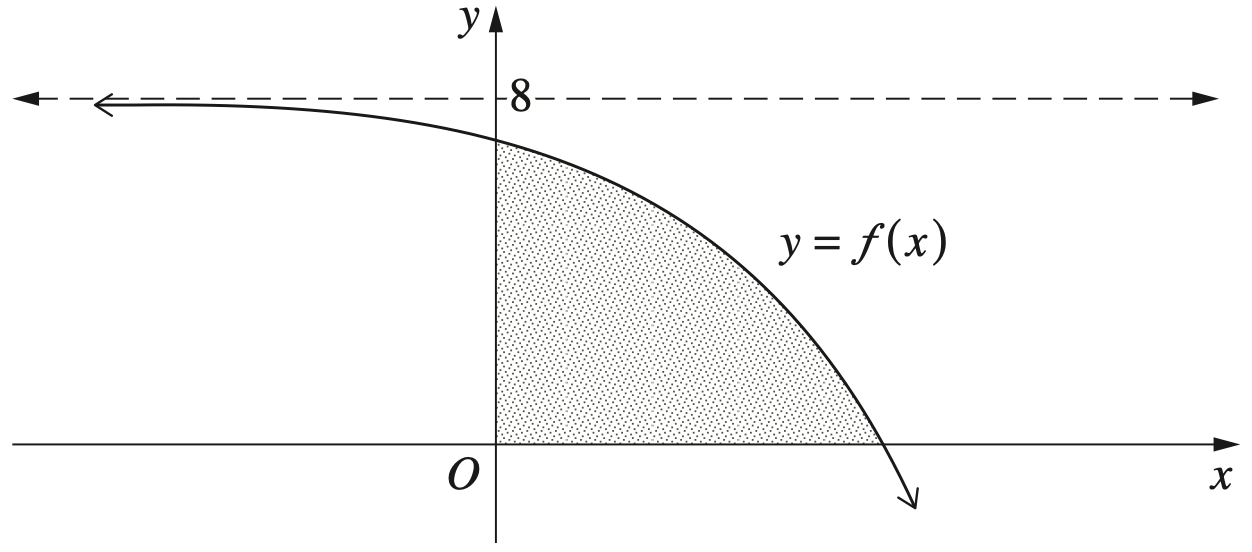
Show that the exact area of the shaded region is given by . (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
A new function is found by taking the graph of and translating it by 5 units to the right.
Sketch the graph of showing the -intercept and the asymptote. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Hence, find the exact value of . (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution





	$²$

♦ Mean mark part (b) 48%.

♦♦♦ Mean mark part (c) 13%.

Calculus, 2ADV C4 2019 HSC 16c

The diagram shows the region , bounded by the curve , where , the -axis and the tangent to the curve at the point .

Show that the tangent to the curve at meets the -axis at

. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Using the result of part (i), or otherwise, show that the area of the region is

. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the exact value of for which the area of is a maximum. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

i.

♦♦ Mean mark part (i) 31%.

ii.

♦♦♦ Mean mark part (ii) 21%.

	`= 1/(r + 1) – 1/2(1 – (r – 1)/r)“

iii.

♦♦ Mean mark part (iii) 23%.

Calculus, 2ADV C4 SM-Bank 12

Let

A right-angled triangle has vertex at the origin, vertex on the -axis and vertex on the graph of , as shown. The coordinates of are

Find the area, , of the triangle in terms of . (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the maximum area of triangle and the value of for which the maximum occurs. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Let be the point on the graph of on the -axis and let be the point on the graph of with the -coordinate .Find the area of the region bounded by the graph of and the line segment . (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$²$
$²$

Show Worked Solution

i.

ii.

♦ Mean mark (Vic) 35%.

$²$

iii.

♦♦ Mean mark (Vic) 32%.





	$²$

Calculus, 2ADV C4 2010 HSC 4b

The curves and intersect at the point as shown in the diagram.

Find the exact area enclosed by the curves and the line . (3 marks)

Show Answer Only

$²$

Show Worked Solutions

MARKER’S COMMENT: The best responses used only a single integral before any substitution as shown in Worked Solutions.





	$²$