The region bounded by the graph of the function `f(x) = 8 - 2^x` and the coordinate axes is shown
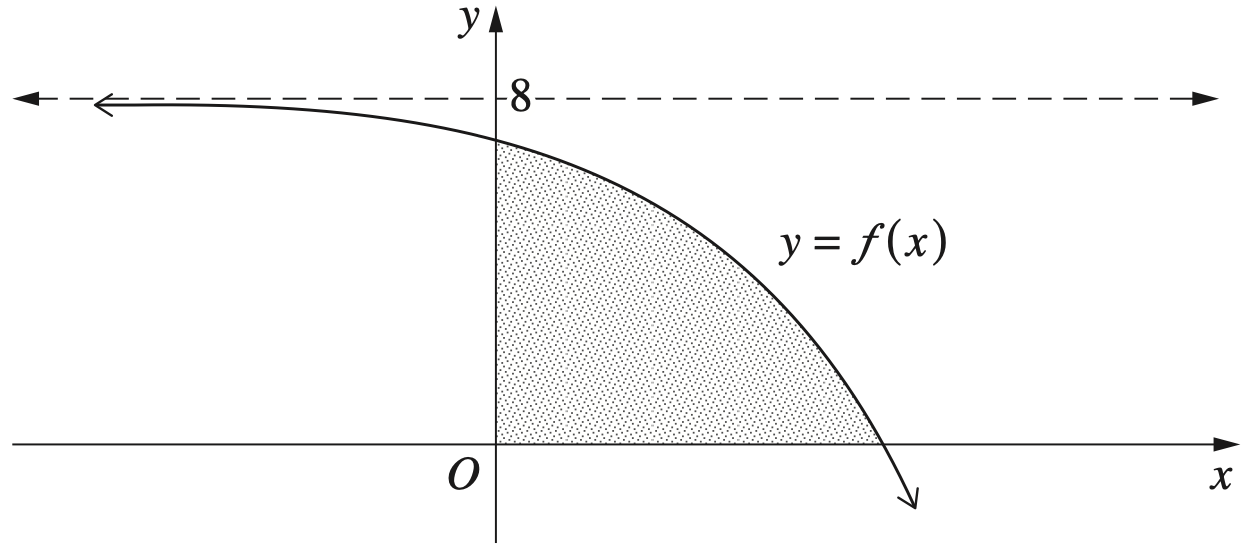
- Show that the exact area of the shaded region is given by `24 - 7/ln2`. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- A new function `g(x)` is found by taking the graph of `y = -f(-x)` and translating it by 5 units to the right.
- Sketch the graph of `y = g(x)` showing the `x`-intercept and the asymptote. (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Hence, find the exact value of `int_2^5 g(x)\ dx`. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Answers Only
- `text(See Worked Solution)`
-
- `7/(ln2) – 24`
Show Worked Solution
a. `xtext(-intercept occurs when)`
`8 – 2^x = 0 \ => \ x = 3`
| `text(Area)` | `= int_0^3 8 – 2^x\ dx` |
| `= [8x – (2^x)/(ln2)]_0^3` | |
| `= 24 – 8/(ln 2) – (0 – 1/(ln2))` | |
| `= 24 – 8/(ln2) + 1/(ln2)` | |
| `= 24 – 7/(ln2)\ \ text(u²)` |
♦ Mean mark part (b) 48%.
b.
`y = f(–x) -> text(reflect)\ \ y = f(x)\ \ text(in the)\ ytext(-axis)`
`y = -f(–x) -> text(reflect)\ \ y = f(–x)\ \ text(in the)\ xtext(-axis)`
♦♦♦ Mean mark part (c) 13%.
c. `int_2^5 g(x)\ dx\ \ text{is the same area as found in part (a)}`
`text(except it is below the)\ xtext(-axis.)`
`:. int_2^5 g(x)\ dx = 7/(ln2) – 24`