SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Volume, SM-Bank 136

  1. What shape best describes the uniform cross-section of this prism?  (1 mark)

  2. Calculate the volume of the prism in cubic centimetres.  (2 marks)
Show Answers Only

a.    \(\text{A rhombus}\)

b.    \(497.664\ \text{cm}^3\)

Show Worked Solution

a.    \(\text{The uniform cross-section is a rhombus.}\)

b.    \(\text{Area of rhombus cross-section }\)

\(A\) \(=\dfrac{1}{2}\times x\times y\)
  \(=\dfrac{1}{2}\times 9.6\times 7.2\)
  \(=34.56\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=34.56\times 14.4\)
  \(=497.664\ \text{cm}^3\)

Volume, SM-Bank 135

The figure below is a prism with a rhombus as the uniform cross-section.

Calculate the value of \(x\), the length of the diagonal in the cross-section, given the volume of the prism is 1950 cubic metres.  (2 marks)

Show Answers Only

\(20\ \text{m}\)

Show Worked Solution

\(\text{The uniform cross-section is a rhombus.}\)

\(\therefore\ A\) \(=\dfrac{1}{2}\times x\times y\)
  \(=\dfrac{1}{2}\times x\times 15\)
  \(=7.5x\ \text{m}^2\)

 

\(V\) \(=A\times h\)
\(1950\) \(=7.5x\times 13\)
\(1950\) \(=97.5x\)
\(\therefore\ x\) \(=\dfrac{1950}{97.5}\)
  \(=20\ \text{m}\)

Volume, SM-Bank 134

The figure below is a prism with a kite as the uniform cross-section.

Calculate the value of \(x\), the length of the diagonal in the cross-section, given the volume of the prism is 1485 cubic centimetres.  (2 marks)

Show Answers Only

\(11\ \text{cm}\)

Show Worked Solution

\(\text{The uniform cross-section is a kite.}\)

\(\therefore\ A\) \(=\dfrac{1}{2}\times x\times y\)
  \(=\dfrac{1}{2}\times x\times 18\)
  \(=9x\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
\(1485\) \(=9x\times 15\)
\(1485\) \(=135x\)
\(\therefore\ x\) \(=\dfrac{1485}{135}\)
  \(=11\ \text{cm}\)

Volume, SM-Bank 133

The figure below is a prism with a parallelogram as the uniform cross-section.

Calculate the value of \(x\), the perpendicular height of the cross-section, given the volume of the prism is 2880 cubic millimetres.  (2 marks)

Show Answers Only

\(12\ \text{mm}\)

Show Worked Solution

\(\text{The uniform cross-section is a parallelogram.}\)

\(\therefore\ A\) \(=b\times h\)
  \(=10\times x\)
  \(=10x\ \text{mm}^2\)

 

\(V\) \(=A\times h\)
\(2880\) \(=10x\times 24\)
\(2880\) \(=240x\)
\(\therefore\ x\) \(=\dfrac{2880}{240}\)
  \(=12\ \text{mm}\)

Volume, SM-Bank 132

  1. What shape best describes the uniform cross-section of this prism?  (1 mark)

  2. Calculate the volume of the prism in cubic centimetres.  (2 marks)
Show Answers Only

a.    \(\text{A parallelogram}\)

b.    \(279.972\ \text{cm}^3\)

Show Worked Solution

a.    \(\text{The uniform cross-section is a parallelogram.}\)

b.    \(\text{Area of parallelogram cross-section }\)

\(A\) \(=b\times h\)
  \(=6.6\times 4.2\)
  \(=27.72\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=27.72\times 10.1\)
  \(=279.972\ \text{cm}^3\)

Volume, SM-Bank 131

  1. What shape best describes the uniform cross-section of this prism?  (1 mark)

  2. Calculate the volume of the prism in cubic metres.  (2 marks)
Show Answers Only

a.    \(\text{A kite}\)

b.    \(28.8\ \text{m}^3\)

Show Worked Solution

a.    \(\text{The uniform cross-section is a kite.}\)

b.    \(\text{Area of kite cross-section }\)

\(A\) \(=\dfrac{1}{2}\times x\times y\)
  \(=\dfrac{1}{2}\times 3\times 4.8\)
  \(=7.2\ \text{m}^2\)

 

\(V\) \(=A\times h\)
  \(=7.2\times 4\)
  \(=28.8\ \text{m}^3\)

Volume, SM-Bank 130

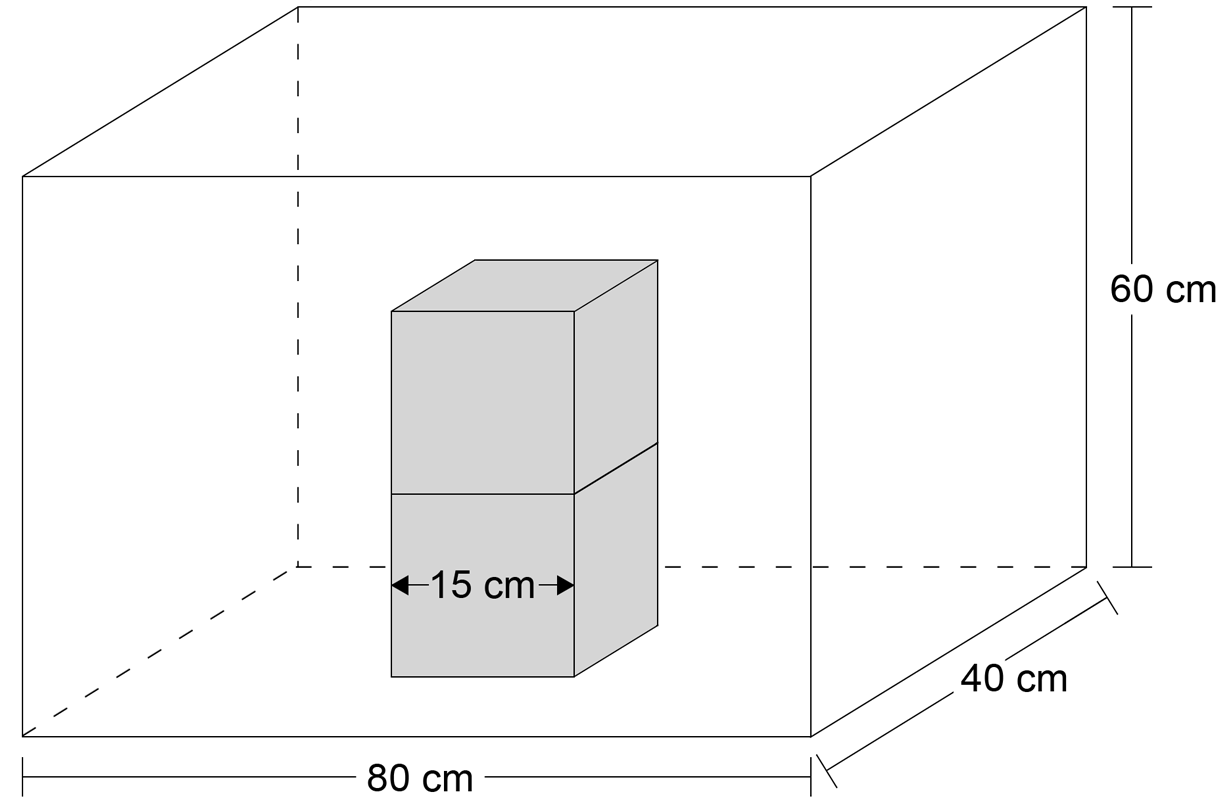
Calculate the volume of the composite prism below in cubic metres.  (2 marks)
 

 
 

Show Answers Only

\(154\ \text{m}^3\)

Show Worked Solution

\(\text{Area of cross-section }(A)\) \(=\ \text{Rectangle 1 – Rectangle 2}\)
  \(=(6\times 3)-(4\times 1)\)
  \(=18-4\)
  \(=14\ \text{m}^2\)

 

\(V\) \(=A\times h\)
  \(=14\times 11\)
  \(=154\ \text{m}^3\)

Volume, SM-Bank 129

Callum has designed a brick with two identical triangular sections removed as shown in the diagram below.
 

 

Calculate the volume of the brick in cubic centimetres.  (2 marks)
Show Answers Only

\(19\ 000\ \text{cm}^3\)

Show Worked Solution

\(\text{Area of cross-section }(A)\) \(=\ \text{Square – 2 × Triangle}\)
  \(=(25\times 25)-2\times \Bigg(\dfrac{1}{2}\times 10\times 15\Bigg)\)
  \(=625-150\)
  \(=475\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=475\times 40\)
  \(=19\ 000\ \text{cm}^3\)

Volume, SM-Bank 128

Calculate the volume of the prism below in cubic centimetres.  (2 marks)
 

 

Show Answers Only

\(896\ \text{cm}^3\)

Show Worked Solution

\(\text{Area of cross-section }(A)\) \(=\ \text{Rectangle – Triangle}\)
  \(=(16\times 10)-\Bigg(\dfrac{1}{2}\times 16\times 6\Bigg)\)
  \(=160-48\)
  \(=112\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=112\times 8\)
  \(=896\ \text{cm}^3\)

Volume, SM-Bank 127

The composite prism below is made up of two right triangular prisms.

Calculate the volume of the composite prism in cubic metres.  (2 marks)
 

Show Answers Only

\(4230\ \text{m}^3\)

Show Worked Solution
\(\text{Area of cross-section }(A)\) \(=\ \text{Triangle 1 + Triangle 2}\)
  \(=\Bigg(\dfrac{1}{2}\times 6\times 18)\Bigg)+\Bigg(\dfrac{1}{2}\times 21\times 15\Bigg)\)
  \(=54+157.5\)
  \(=211.5\ \text{m}^2\)

 

\(V\) \(=A\times h\)
  \(=211.5\times 20\)
  \(=4230\ \text{m}^3\)

Volume, SM-Bank 126

Calculate the volume of the composite prism below, giving your answer in cubic centimetres.  (2 marks)
 

Show Answers Only

\(7.182\ \text{cm}^3\)

Show Worked Solution

\(\text{Convert measurements from mm to cm before calculations}\)

\(\text{Area of cross-section }\) \(=\ \text{Trapezium + Triangle}\)
  \(=\Bigg(\dfrac{0.9}{2}\times(2.4+1.2)\Bigg)+\Bigg(\dfrac{1}{2}\times 2.4\times 1.5\Bigg)\)
  \(=1.62+1.8\)
  \(=3.42\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=3.42\times 2.1\)
  \(=7.182\ \text{cm}^3\)

Volume, SM-Bank 125

Ben is designing blocks for a children's game. The block below is in the shape of a right prism and the dimensions are shown in the diagram.
 

Calculate the volume of the block in cubic centimetres.  (3 marks)
Show Answers Only

\(0.594\ \text{m}^3\)

Show Worked Solution

\(\text{Area of cross-section }\) \(=\ \text{Rectangle + Triangle}\)
  \(=(8\times 6)+(\dfrac{1}{2}\times 6\times 4)\)
  \(=48+12\)
  \(=60\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=60\times 7\)
  \(=420\ \text{cm}^3\)

Volume, SM-Bank 124

The local council builds a concrete bench in a public park. The bench is in the shape of a prism and the dimensions are shown in the diagram below.
 

Calculate the volume of the bench in cubic metres.  (3 marks)
Show Answers Only

\(0.594\ \text{m}^3\)

Show Worked Solution

\(\text{Convert measurements from cm to m before calculations}\)

\(\text{Area of cross-section }\) \(=\ \text{Rectangle + Triangle}\)
  \(=(0.6\times 0.75)+(\dfrac{1}{2}\times 0.3\times 0.3)\)
  \(=0.45+0.045\)
  \(=0.495\ \text{m}^2\)

 

\(V\) \(=A\times h\)
  \(=0.495\times 1.2\)
  \(=0.594\ \text{m}^3\)

Volume, SM-Bank 123

Calculate the volume of the prism below in cubic metres.  (2 marks)

Show Answers Only

\(540\ \text{m}^3\)

Show Worked Solution
\(\text{Area of cross-section}\) \(=(9\times 8)-(3\times 6)\)
  \(=72-18\)
  \(=54\ \text{m}^2\)

 

\(V\) \(=A\times h\)
  \(=54\times 10\)
  \(=540\ \text{m}^3\)

Volume, SM-Bank 122

Calculate the capacity of the prism below in litres.  (2 marks)

Show Answers Only

\(140\ 000\ \text{L}\)

Show Worked Solution
\(V\) \(=A\times h\)
  \(=14\times 10\)
  \(=140\ \text{m}^3\)

 
\(\text{1 m}^3=\text{1000 L}\)

 \(\therefore\ \text{Capacity}\) \(=140\times 1000\ \text{L}\)
  \(=140\ 000\ \text{L}\)

Volume, SM-Bank 121

The prism above is a triangular prism.

  1. Calculate the volume of the prism in cubic centimetres.  (2 marks)

  2. Calculate the capacity of the prism in litres.  (1 mark)
Show Answers Only

a.    \(103.23\ \text{cm}^3\)

b.    \(0.10323\ \text{L}\)

Show Worked Solution

a.    \(\text{Note: Convert mm to cm before calculations}\)

\(\text{Cross-sectional area}(A)\) \(=\dfrac{1}{2}\times b\times h\)
  \(=\dfrac{1}{2}\times 6.2\times 4.5\)
  \(=13.95\ \text{cm}^2\)

 

\(V\) \(=A\times h\)
  \(=13.95\times 7.4\)
  \(=103.23\ \text{cm}^3\)

 
b.    \(\text{1 L}=\text{1000 cm}^3\)

 \(\text{Capacity}\) \(=\dfrac{103.23}{1000}\ \text{L}\)
  \(=0.10323\ \text{L}\)

Volume, SM-Bank 120

The prism above is a rectangular prism.

  1. Calculate the volume of the prism in cubic metres.  (2 marks)

  2. Calculate the capacity of the prism in litres.  (1 mark)
Show Answers Only

a.    \(15\ \text{m}^3\)

b.    \(15\ 000\ \text{L}\)

Show Worked Solution

a.    \(\text{Note: Convert cm to m before calculations}\)

\(V\) \(=l\times b\times h\)
  \(=2\times 5\times 1.5\)
  \(=15\ \text{m}^3\)

 
b.    \(\text{1 m}^3=\text{1000 L}\)

 \(\text{Capacity}\) \(=15\times 1000\ \text{L}\)
  \(=15\ 000\ \text{L}\)

Volume, SM-Bank 096

Guy builds a brick structure that is pictured below.

The structure is 7 bricks high, 7 bricks wide and 6 bricks deep.

The structure is solid brick but has a hole that goes from one side to the other which is 3 bricks high and two bricks wide, as shown in the diagram.
 

 
How many bricks are in the stack?  (2 marks)

Show Answers Only

\(258\ \text{bricks}\)

Show Worked Solution

\(\text{Bricks in the stack if no hole}\)

\(=7\times 7\times 6\)

\(=294\)

\(\text{Bricks removed to make hole}\)

\(=3\times 2\times 6\)

\(=36\)

\(\therefore\ \text{Bricks in stack}\) \(=294-36\)
  \(=258\)

Volume, SM-Bank 095

A horse trough is in the shape of a rectangular prism, pictured below.
 

  1.  What is the volume of the prism in cubic centimetres?  (2 marks)
  2. What is the capacity of the horse trough in litres?  (1 mark)
Show Answers Only

a.    \(160\ 000\ \text{cm}^3\)

b.    \(160\ \text{L}\)

Show Worked Solution
a.    \(\text{Volume}\) \(=Ah\)
    \(=(40\times 50)\times 80\)
    \(=160\ 000\ \text{cm}^3\)

  
b.    \(1000\ \text{cm}^3=1\ \text{Litre}\)

\(\therefore\ \text{Capacity}\) \(=\dfrac{160\ 000}{1000}\)
  \(=160\ \text{L}\)

Volume, SM-Bank 094

Two identical solid cubes are placed at the bottom of a fish tank.
 

 

The fish tank is then completely filled, as shown below.

What is the volume of the water that surrounds the cubes?

Give your answer in cubic centimetres.  (2 marks)

Show Answers Only

\(185\ 250\ \text{cm}^3\)

Show Worked Solution
\(\text{Volume of tank}\) \(=l\times b\times h\)
  \(=80\times 60\times 40\)
  \(=192\ 000\ \text{cm}^3\)

 

\(\text{Volume of cubes}\) \(=2\times s^3\)
  \(=2\times 15^3\)
  \(=6750\ \text{cm}^3\)

 

\(\therefore\ \text{Volume of water}\) \(=192\ 000-6750\)
  \(=185\ 250\ \text{cm}^3\)

Volume, SM-Bank 093

Two views of a trapezoidal prism are shown below.
 

Each square on this grid has an area of one square centimetre.

The vertical edges of the prism are 5 centimetres.

  1. What is the area of the shaded cross-section in square centimetres?  (2 marks)
  2. What is the volume of the prism in cubic centimetres?  (2 marks)
Show Answers Only

a.    \(20\ \text{cm}^2\)

b.    \(100\ \text{cm}^3\)

Show Worked Solution

a.    \(\text{The area of the cross-section (trapezium)}\)

\(=14\ \text{squares}+8\ \text{triangles}\ (1\times 1) + 1\ \text{triangle}\ (1\times 4)\)

\(=14+(8\times \dfrac{1}{2})+2\)

\(=20\ \text{cm}^2\)
 

b.    \(\text{Volume}\) \(=Ah\)
    \(=20\times 5\)
    \(=100\ \text{cm}^3\)

Volume, SM-Bank 092

Two views of a trapezoidal prism are shown below.

Each square on this grid has an area of one square centimetre.

The vertical edges of the prism are 4 centimetres.

  1. What is the area of the shaded cross-section in square centimetres?  (2 marks)
  2. What is the volume of the prism in cubic centimetres?  (2 marks)
Show Answers Only

a.    \(18\ \text{cm}^2\)

b.    \(72\ \text{cm}^3\)

Show Worked Solution

a.    \(\text{The area of the cross-section (trapezium)}\)

\(=12\ \text{squares}+9\ \text{triangles}\ (1\times 1) + 1\ \text{triangle}\ (1\times 3)\)

\(=12+(9\times \dfrac{1}{2})+1\dfrac{1}{2}\)

\(=18\ \text{cm}^2\)
 

b.    \(\text{Volume}\) \(=Ah\)
    \(=18\times 4\)
    \(=72\ \text{cm}^3\)

Volume, SM-Bank 091

An ancient building has the shape of a trapezoidal prism.

The shaded side is a trapezium.
 

 
What is the volume of the building in m³ ?  (2 marks)

Show Answers Only

\(1344\ \text{m}^3\)

Show Worked Solution

\(\text{Area of trapezium}\)

\(A\) \(=\dfrac{h}{2}\times (a+b)\)
  \(=\dfrac{6}{2}\times (12+16)\)
  \(=3\times 28\)
  \(=84\ \text{m}^2\)

 

\(\therefore\ V\) \(=Ah\)
  \(=84\times 16\)
  \(=1344\ \text{m}^3\)

Volume, SM-Bank 090

A rectangular trough in a paddock provides water for horses.

Its measurements can be seen below:
  

  1. Calculate the volume of the trough in cubic metres.  (2 marks)
  2. Given that one cubic metre holds 1000 litres of water, what is the capacity of the trough in litres?  (1 mark)

Show Answers Only

a.    \(3\ \text{m}^3\)

b.    \(\text{3000 litres}\)

Show Worked Solution
a.    \(\text{Volume}\) \(=Ah\)
    \(=(0.5\times 0.75)\times 8\)
    \(=0.375\times 8\)
    \(=3\ \text{m}^3\)

 

b.    \(\text{Capacity}\) \(=1000\times 3\)
    \(=3000\ \text{litres}\)

Volume, SM-Bank 089

A large sculpture is made in the shape of a cube.

The total length of all of its edges is 60 metres.

What is the volume of the cube in cubic metres?  (2 marks)

Show Answers Only

\(125\ \text{m}^3\)

Show Worked Solution

\(\text{A cube has 12 edges.}\)

\(\text{Length of 1 edge} =\dfrac{60}{12} = 5\ \text{m}\)
 

\(\therefore\ \text{Volume of cube}\) \(=5\times 5\times 5\)
  \(=125\ \text{m}^3\)

Volume, SM Bank 088 MC

Alan is moving house and is packing his belongings in rectangular cardboard boxes.

The height of each box is 0.5 metres.

Which box has a volume of 0.12 cubic metres?
 

 

Show Answers Only

\(D\)

Show Worked Solution

\(\text{Volume}\)

\(=0.4\times 0.6\times 0.5\)

\(= 0.12\ \text{m}^3\)

\(\Rightarrow D\)

Volume, SM-Bank 087 MC

Two bricks can be joined to make three different rectangular prisms. Two of them are shown here.
 

 
What would be the measurements of the third prism?

  1. 18 cm by 16 cm by 7 cm
  2. 36 cm by 8 cm by 7 cm
  3. 32 cm by 18 cm by 7 cm
  4. 36 cm by 14 cm by 8 cm
Show Answers Only

\(B\)

Show Worked Solution

\(\text{36 cm by 8 cm by 7 cm}\)
 

\(\Rightarrow B\)

Volume, SM-Bank 080

Wes made a small model staircase by stacking blocks.

There are no gaps between blocks.
 

 If each block is 1 cubic centimetre, what is the volume of the model staircase?  (2 marks)

Show Answers Only

\(80\ \text{cm}^2\)

Show Worked Solution

\(\text{Area of cross-section = 20 cm}^2\)

\(V\) \(=Ah\)
  \(=20\times 4\)
  \(=80\ \text{cm}^3\)

 
\(\therefore\ \text{The volume of the model staircase = 80 cm}^3\)

Volume, SM-Bank 066

Gavin is going camping in the summer holidays and purchased the two-person tent shown below.

  1. Given the triangular face of the tent is isosceles, use Pythagoras' Theorem to calculate the perpendicular height of the tent.  (2 marks)
  2. Using your answer from (a), calculate the volume of the tent in cubic metres.  (2 marks)
  3. What is the capacity of the tent in litres?  (1 mark)
Show Answers Only

a.    \(2\ \text{m}\)

b.    \(12 \text{m}^3\)

c.    \(12\ 000\ \text{L}\)

Show Worked Solution
a.    \(a^2+b^2\) \(=c^2\)
  \(x^2+1.5^2\) \(=2.5^2\)
  \(x^2\) \(=2.5^2-1.5^2\)
  \(x^2\) \(=4\)
  \(x\) \(=\sqrt{4}=2\)

 
\(\therefore\ \text{The perpendicular height of the tent is }2\ \text{metres.}\)
 

b.    \(V\) \(=Ah\)
    \(=\Big(\dfrac{1}{2}\times 3\times 2\Big)\times 4\)
    \(=3\times 4\)
    \(=12\ \text{m}^3\)

 

c.    \(1\ \text{m}^3\) \(=1000\ \text{L}\)
  \(\therefore\ 12\ \text{m}^3\) \(=12\ 000\ \text{L}\)

  
\(\therefore\ \text{The capacity of the tent is }12\ 000\ \text{litres.}\)

Volume, SM-Bank 065

  1. Given the triangular face of the prism above is isosceles, use Pythagoras' Theorem to calculate its perpendicular height. Give your answer correct to the nearest whole centimetre.  (2 marks)
  2. Using your answer from (a), calculate the volume of the prism in cubic centimetres.  (2 marks)
Show Answers Only

a.    \(7\ \text{cm}\)

b.    \(168\ \text{cm}^3\)

Show Worked Solution
a.    \(a^2+b^2\) \(=c^2\)
  \(a^2+3^2\) \(=7.6^2\)
  \(a^2\) \(=7.6^2-3^2\)
  \(a^2\) \(=48.76\)
  \(a\) \(=\sqrt{48.76}=6.982\dots\)
  \(a\) \(\approx 7\)

 
\(\therefore\ \text{The perpendicular height of the triangle is }7\ \text{cm, (nearest whole centimetre).}\)
 

b.    \(V\) \(=Ah\)
    \(=\Big(\dfrac{1}{2}\times 6\times 7\Big)\times 8\)
    \(=21\times 8\)
    \(=168\ \text{cm}^3\)

Volume, SM-Bank 064

  1. For the triangular prism above, use Pythagoras' Theorem to calculate the perpendicular height, \(x\), of the triangular face.  (2 marks)
  2. Using your answer from (a), calculate the volume of the prism in cubic millimetres.  (2 marks)
Show Answers Only

a.    \(5\ \text{mm}\)

b.    \(480\ \text{mm}^3\)

Show Worked Solution
a.    \(a^2+b^2\) \(=c^2\)
  \(x^2+12^2\) \(=13^2\)
  \(x^2\) \(=13^2-12^2\)
  \(x^2\) \(=25\)
  \(x\) \(=\sqrt{25}=5\)

 
\(\therefore\ \text{The perpendicular height of the triangle is }5\ \text{mm}\)
 

b.    \(V\) \(=Ah\)
    \(=\Big(\dfrac{1}{2}\times 12\times 5\Big)\times 16\)
    \(=30\times 16\)
    \(=480\ \text{mm}^3\)

Volume, SM-Bank 063

Calculate the volume of the triangular prism below in cubic metres.  (2 marks)

Show Answers Only

\(648\ \text{m}^3\)

Show Worked Solution
\(V\) \(=Ah\)
  \(=\Big(\dfrac{1}{2}\times 8\times 9\Big)\times 18\)
  \(=36\times 18\)
  \(=648\ \text{m}^3\)

Volume, SM-Bank 062

Calculate the volume of the triangular prism below in cubic centimetres.   (2 marks) 
 

Show Answers Only

\(102.362\ \text{cm}^3\)

Show Worked Solution
\(V\) \(=Ah\)
  \(=\Big(\dfrac{1}{2}\times 3.1\times 5.2\Big)\times 12.7\)
  \(=8.06\times 12.7\)
  \(=102.362\ \text{cm}^3\)

Volume, SM-Bank 061

Calculate the volume of the triangular prism below in cubic metres.  (2 marks)

Show Answers Only

\(105\ \text{m}^3\)

Show Worked Solution
\(V\) \(=Ah\)
  \(=\Big(\dfrac{1}{2}\times 6\times 5\Big)\times 7\)
  \(=15\times 7\)
  \(=105\ \text{m}^3\)

Volume, SM-Bank 060

A children's rectangular swimming pool measures 175 cm × 180 cm × 30 cm.

  1. Find the volume of the swimming pool in cubic centimetres.  (2 marks)

  2. What is the capacity of the swimming pool in litres?  (1 mark)

Show Answers Only

a.    \(945\ 000\ \text{cm}^3\)

b.    \(945\ \text{L}\)

Show Worked Solution
a.     \(V\) \(=Ah\)  
    \(=(175\times 180)\times 30\)
    \(=945\ 000\ \text{cm}^3\)

 
b.    \(1\ \text{L}=1000\ \text{cm}^3\)

\(945\ 000\ \text{cm}^3\) \(=\Bigg(\dfrac{945\ 000}{1000}\Bigg)\ \text{L}\)
  \(=945\ \text{L}\)

 
\(\therefore\ \text{The swimming pool will hold 945 litres of water.}\)

Volume, SM-Bank 059

During the construction of a new house a concrete slab in the shape of a rectangular prism is to be poured.

The slab measures 20 m × 15 m × 0.15 m.

  1. Find the volume of the concrete required for the slab in cubic metres.  (2 marks)

  2. Calculate the cost of the concrete if it costs $350 per cubic metre.  (2 marks)

Show Answers Only

a.    \(45\ \text{m}^3\)

b.    \($15\ 750\)

Show Worked Solution
a.     \(V\) \(=Ah\)  
  \(V\) \(=(20\times 15)\times 0.15\)
    \(=45\ \text{m}^3\)

 

b.    \(\text{Cost}\) \(=\text{Price}\times \text{Concrete}\)
    \(=$350\times 45\)
    \(=$15\ 750\)

Volume, SM-Bank 058

A rectangular sand pit measures 150 cm × 200 cm × 45 cm.

  1. Find the volume of the sand pit in cubic centimetres.  (2 marks)

  2. How many cubic metres of sand will the sand pit hold?  (1 mark)

Show Answers Only

a.    \(1\ 350\ 000\ \text{cm}^3\)

b.    \(1.35\ \text{m}^3\)

Show Worked Solution
a.     \(V\) \(=Ah\)  
  \(V\) \(=(150\times 200)\times 45\)
    \(=1\ 350\ 000\ \text{cm}^3\)

 
b.    \(1\ \text{m}=100\ \text{cm}\)

\(\therefore\ 1\ \text{m}^3=(100\times 100\times 100)\ \text{cm}^3\)

\(\therefore\ 1\ 350\ 000\ \text{cm}^3\) \(=\Bigg(\dfrac{1\ 350\ 000}{100\times 100\times 100}\Bigg)\ \text{m}^3\)
  \(=1.35\ \text{m}^3\)

 
\(\therefore\ \text{The sandpit will hold }1.35\ \text{cubic metres of sand.}\)

Volume, SM-Bank 057

Calculate the volume of the rectangular prism below in cubic millimetres.   (2 marks)
 

Show Answers Only

\(104\ 832\ \text{mm}^3\)

Show Worked Solution
\(V\) \(=Ah\)
\(V\) \(=(39\times 42)\times 64\)
  \(=104\ 832\ \text{mm}^3\)

Volume, SM-Bank 056

Calculate the volume of the rectangular prism below in cubic centimetres.  (2 marks)
 

Show Answers Only

\(402.57\ \text{cm}^3\)

Show Worked Solution
\(V\) \(=Ah\)
\(V\) \(=(4.2\times 13.5)\times 7.1\)
  \(=402.57\ \text{cm}^3\)

Volume, SM-Bank 055

Calculate the volume of the rectangular prism below in cubic metres.  (2 marks)
 

Show Answers Only

\(360\ \text{m}^3\)

Show Worked Solution
\(V\) \(=Ah\)
\(V\) \(=(5\times 9)\times 8\)
  \(=360\ \text{m}^3\)

Volume, SM-Bank 047

A shipping container in the shape of a rectangular prism is being transported by truck to a construction site.

The dimensions of the container are marked on the diagram below and are in metres.
 

  1. Calculate the volume of the shipping container in cubic metres.   (2 marks)

  2. The shipping container is to be converted into a small lap pool on site.
    Calculate the capacity of the lap pool when full, giving your answer in kilolitres?       (1 mark)

Show Answers Only

a.    \(8.1\ \text{m}^3\)

b.    \(8.1\ \text{kL}\)

Show Worked Solution
a.     \(V\) \(=Ah\)
  \(V\) \(=1.8\times 1.5\times 3\)
    \(=8.1\ \text{m}^3\)

  
b.    \(1\ \text{m}^3=1\ \text{kL}\)

\(\therefore\ 8.1\ \text{m}^3=8.1\ \text{kL}\)

\(\therefore\ \text{Capacity of the lap pool when full is }8.1\ \text{kilolitres.}\)

Volume, SM-Bank 046

A fish tank is in the shape of a cube with a side length of 20 centimetres.
 

  1. Calculate the volume of the fish tank in cubic centimetres.  (2 marks)

  2. What is the capacity of the fish tank in litres?  (1 mark)

Show Answers Only

a.    \(8000\ \text{cm}^3\)

b.    \(8\ \text{litres}\)

Show Worked Solution
a.     \(V\) \(=Ah\)
    \(=20\times 20\times 20\)
    \(=8\ 000\ \text{cm}^3\)

  
b.    \(1000\ \text{cm}^3=1\ \text{litre}\)

\(8000\ \text{cm}^3=8\ \text{litres}\)

\(\therefore\ \text{Capacity of fish tank is }8\ \text{litres.}\)

Volume, SM-Bank 045

A packing box is in the shape of a cube with a side length of 40 centimetres.
 

Calculate the volume of the packing box in cubic metres.  (2 marks)

Show Answers Only

\(0.64\ \text{m}^3\)

Show Worked Solution

\(\text{Convert measurements to metres before substituting into formula.}\)

\(100\ \text{cm}=1\ \text{m}\)

\(\therefore\ 40\ \text{cm}=0.40\ \text{m}\)

\(\text{Volume}\) \(=Ah\)
\(V\) \(=0.40\times 0.40\times 0.40\)
  \(=0.64\ \text{m}^3\)

Volume, SM-Bank 044

A paper recycling bag is in the shape of a cube with a side length of 0.5 metres.
 

Estimate the volume of the recycling bag in cubic metres.  (2 marks)

Show Answers Only

\(0.125\ \text{m}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
\(V\) \(=0.5\times 0.5\times 0.5\)
  \(=0.125\ \text{m}^3\)

Volume, SM-Bank 043

A cooking vat in the shape of a cube has a volume of 1.331 cubic metres.

Calculate the side length of the vat.  (2 marks)

Show Answers Only

\(1.1\ \text{m}\)

Show Worked Solution

\(\text{Let }s \ \text{be the side length of the cube}\)

\(\text{Volume}\) \(=Ah\)
\(1.331\) \(=s\times s\times s\)
\(s^3\) \(=1.331\)
\(s\) \(=\sqrt[3]{1.331}\)
  \(=1.1\)

 
\(\therefore\ \text{Side length of the vat is 1.1 metres.}\)

Volume, SM-Bank 042

Find the side length of a cube with a volume of 0.343 cubic metres.  (2 marks)

Show Answers Only

\(0.7\ \text{m}\)

Show Worked Solution

\(\text{Let }s \ \text{be the side length of the cube}\)

\(\text{Volume}\) \(=Ah\)
\(0.343\) \(=s\times s\times s\)
\(s^3\) \(=0.343\)
\(s\) \(=\sqrt[3]{0.343}\)
  \(=0.7\)

 
\(\therefore\ \text{Side length of the cube is }0.7\ \text{metres.}\)

Volume, SM-Bank 041

Find the side length of a cube with a volume of 117 649 cubic centimetres.   (2 marks)

Show Answers Only

\(49\ \text{cm}\)

Show Worked Solution

\(\text{Let }s \ \text{be the side length of the cube}\)

\(\text{Volume}\) \(=Ah\)
\(117\ 649\) \(=s\times s\times s\)
\(s^3\) \(=117\ 649\)
\(s\) \(=\sqrt[3]{117\ 649}\)
  \(=49\)

 
\(\therefore\ \text{Side length of the cube is 49 centimetres.}\)

Volume SM-Bank 040

Find the side length of a cube with a volume of 27 cubic millimetres.  (2 marks)

Show Answers Only

\(3\ \text{mm}\)

Show Worked Solution

\(\text{Let }s \ \text{be the side length of the cube}\)

\(\text{Volume}\) \(=Ah\)
\(27\) \(=s\times s\times s\)
\(s^3\) \(=27\)
\(s\) \(=\sqrt[3]{27}\)
  \(=3\)

 
\(\therefore\ \text{Side length of the cube is }3\ \text{millimetres.}\)

Volume, SM-Bank 039

Calculate the volume of a cube with a side length of 21 millimetres.  (2 marks)

Show Answers Only

\(9261\ \text{mm}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=21\times 21\times 21\)
  \(=9261\ \text{mm}^3\)

Volume, SM-Bank 038

Calculate the volume of a cube with a side length of 9 metres.  (2 marks)

Show Answers Only

\(729\ \text{m}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=9\times 9\times 9\)
  \(=729\ \text{m}^3\)

Volume, SM-Bank 037

Calculate the volume of a cube with a side length of 3.6 metres.   (2 marks)

Show Answers Only

\(46.656\ \text{m}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=3.6\times 3.6\times 3.6\)
  \(=46.656\ \text{m}^3\)

Volume, SM-Bank 036

Calculate the volume of a cube with a side length of 4 centimetres.  (2 marks)

Show Answers Only

\(64\ \text{cm}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=4\times 4\times 4\)
  \(=64\ \text{cm}^3\)

Volume, SM-Bank 035

Calculate the volume of the cube below in cubic metres.   (2 marks)
  

  

Show Answers Only

\(15.625\ \text{m}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=2.5\times 2.5\times 2.5\)
  \(=15.625\ \text{m}^3\)

Volume, SM-Bank 034

Calculate the volume of the cube below in cubic millimetres.  (2 marks)
  

  

Show Answers Only

\(3.375\ \text{mm}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=1.5\times 1.5\times 1.5\)
  \(=3.375\ \text{mm}^3\)

Volume, SM-Bank 033

Calculate the volume of the cube below in cubic metres.  (2 marks)
  

  

Show Answers Only

\(8\ \text{m}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=2\times 2\times 2\)
  \(=8\ \text{m}^3\)

Volume, SM-Bank 032

Calculate the volume of the cube below in cubic centimetres.  (2 marks)
  

  

Show Answers Only

\(1728\ \text{cm}^3\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=12\times 12\times 12\)
  \(=1728\ \text{cm}^3\)

Volume, SM-Bank 031 MC

A timber door wedge is pictured below.
 

The wedge is in the shape of a triangular prism.

What is the volume of the wedge in cubic centimetres?

  1. \(7.5\ \text{cm}^3\)
  2. \(37.5\ \text{cm}^3\)
  3. \(75\ \text{cm}^3\)
  4. \(375\ \text{cm}^3\)
Show Answers Only

\(B\)

Show Worked Solution

\(\text{10 mm =1 cm}\)

\(\text{Volume}\) \(=Ah\)
  \(=\bigg(\dfrac{1}{2}\times 10\times 3\bigg)\times 2.5\)
  \(=15\times 2.5\)
  \(=37.5\ \text{cm}^3\)

 
\(\Rightarrow\ B\)

Volume, SM-Bank 030 MC

A wheelchair ramp is pictured below.
  

 
The ramp is in the shape of a triangular prism.

What is the volume of the ramp?

  1. \(2.8\ \text{m}^3\)
  2. \(5.6\ \text{m}^3\)
  3. \(0.28\ \text{m}^3\)
  4. \(0.56\ \text{m}^3\)
Show Answers Only

\(A\)

Show Worked Solution
\(\text{Volume}\) \(=Ah\)
  \(=(\dfrac{1}{2}\times 7\times 0.4)\times 2\)
  \(=1.4\times 2\)
  \(=2.8\ \text{m}^3\)

 
\(\Rightarrow\ A\)

Volume, SM-Bank 029 MC

Concrete is poured to make a pathway.

The dimensions of the slab are shown in the diagram below.
 

If the concrete costs $180 per cubic metre to pour, what is the cost of pouring the slab?

  1. \($864\)
  2. \($2880\)
  3. \($22\ 600\)
  4. \($86\ 400\)
Show Answers Only

\(A\)

Show Worked Solution

\(30\ \text{cm}=0.3\ \text{m}\)

\(\text{Volume of slab}\) \(=8\times 0.3\times 2\)
  \(=4.8\ \text{m}^3\)

 

\(\text{Cost of pouring slab}\) \(=4.8\times $180\)
  \(=$864\)

\(\Rightarrow\ A\)

Volume, SM-Bank 028

A kitchen sink is in the shape of a rectangular prism.

Its measurements can be seen below:

If one cubic metre holds 1000 litres of water, how many litres of water will it take to fill the kitchen sink? 

Give your answer correct to the nearest litre.  (2 marks)

Show Answers Only

\(38\ \text{litres (nearest L)}\)

Show Worked Solution
\(\text{Volume of kitchen sink}\) \(=0.44\times 0.36\times 0.24\)
  \(=0.038\ 016\ \text{m}^3\)
   
\(\text{Capacity of kitchen sink}\) \(=0.038\ 016\times 1000\)
  \(=38.016\)
  \(\approx 38\ \text{litres (nearest L)}\)