Non Right-Angled Trig

Trigonometry, SMB-067

Find the value of \(\theta\), correct to the nearest minute. (3 marks)

Show Answers Only

\(\theta=112^{\circ} 12^{′}\)

Show Worked Solution

\(\cos A\)	\(= \dfrac{b^2+c^2-a^2}{2bc} \)
\(\cos \theta\)	\(= \dfrac{7.8^2+10.2^2-15.0^2}{2 \times 7.8 \times 10.2}\)
	\(= -0.3778…\)
\(\therefore \theta\)	\(= \cos^{-1} (-0.3778…) \)
	\(=112.199…^{\circ} \)
	\(=112^{\circ} 12^{′}\ \ \text{(nearest minute)} \)

Trigonometry, SMB-066

Find the value of \(\theta\), correct to the nearest degree. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

\(\theta=35^{\circ}\)

Show Worked Solution

\(\cos A\)	\(= \dfrac{b^2+c^2-a^2}{2bc} \)
\(\cos \theta\)	\(= \dfrac{16.2^2+18.1^2-10.5^2}{2 \times 16.2 \times 18.1}\)
	\(= 0.818…\)
\(\therefore \theta\)	\(= \cos^{-1} (0.818…) \)
	\(=35.09…^{\circ} \)
	\(=35^{\circ}\ \ \text{(nearest degree)} \)

Trigonometry, SMB-065

Find the value of \(\theta\), correct to 1 decimal place. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

\(\theta=38.9^{\circ}\)

Show Worked Solution

\(\cos A\)	\(= \dfrac{b^2+c^2-a^2}{2bc} \)
\(\cos \theta\)	\(= \dfrac{9^2+5^2-6^2}{2 \times 9 \times 5}\)
	\(= 0.777…\)
\(\therefore \theta\)	\(= \cos^{-1} (0.777…) \)
	\(=38.94…^{\circ} \)
	\(=38.9^{\circ}\ \ \text{(1 d.p.)} \)

Trigonometry, SMB-064

Find the value of \(d\), correct to 2 decimal places. (3 marks)

Show Answers Only

\(d=12.9\ \text{km}\)

Show Worked Solution

\(a^2\)	\(=b^2+c^2-2bc\ \cos A \)
\(d^2\)	\(= 8.9^2+5.2^2-2 \times 8.9 \times 5.2 \times \cos 130^{\circ}\)
	\(= 165.746…\)
\(\therefore d\)	\(=12.87…\)
	\(=12.9\ \text{km (1 d.p.)} \)

Trigonometry, SMB-063

Find the value of \(x\), correct to 1 decimal place. (3 marks)

Show Answers Only

\(x=15.4\ \text{cm}\)

Show Worked Solution

\(a^2\)	\(=b^2+c^2-2bc\ \cos A \)
\(x^2\)	\(= 15^2+25^2-2 \times 15 \times 25 \times \cos 35^{\circ}\)
	\(= 235.63…\)
\(\therefore x\)	\(=15.35…\)
	\(=15.4\ \text{cm (1 d.p.)} \)

Trigonometry, SMB-062

Find the value of \(x\), correct to 1 decimal place. (3 marks)

Show Answers Only

\(x=8.8\ \text{m}\)

Show Worked Solution

\(a^2\)	\(=b^2+c^2-2bc\ \cos A \)
\(x^2\)	\(= 5^2+9^2-2 \times 5 \times 9 \times \cos 72^{\circ}\)
	\(= 78.188…\)
\(\therefore x\)	\(=8.842…\)
	\(=8.8\ \text{m (1 d.p.)} \)

Trigonometry, SMB-061

Find the value of \(\theta\), correct to the nearest degree. (3 marks)

Show Answers Only

\(\theta=154^{\circ}\)

Show Worked Solution

\(\dfrac{\sin \theta}{21}\)	\(= \dfrac{\sin 12^{\circ}}{10} \)
\(\sin \theta\)	\(= \dfrac{21 \times \sin 12^{\circ}}{10}\)
\(\theta\)	\(=\sin^{-1} (0.4366) \)
	\(=25.88…^{\circ} \)
	\(=26^{\circ}\ \text{(nearest degree)} \)

\(\therefore\ \theta = 180-26=154^{\circ}\ \ \text{(angle is obtuse)}\)

Trigonometry, SMB-060

Find the value of \(\alpha\), correct to the nearest degree. (2 marks)

Show Answers Only

\(\alpha=39^{\circ}\)

Show Worked Solution

\(\dfrac{\sin \alpha}{9}\)	\(= \dfrac{\sin 79^{\circ}}{14} \)
\(\sin \alpha\)	\(= \dfrac{9 \times \sin 79^{\circ}}{14}\)
\(\alpha\)	\(=\sin^{-1} (0.6310) \)
	\(=39.12…^{\circ} \)
	\(=39^{\circ}\ \text{(nearest degree)} \)

Trigonometry, SMB-059

Find the value of \(\theta\), correct to the nearest degree. (2 marks)

Show Answers Only

\(\theta=50^{\circ}\)

Show Worked Solution

\(\dfrac{\sin \theta}{7.5}\)	\(= \dfrac{\sin 66^{\circ}}{8.9} \)
\(\sin \theta\)	\(= \dfrac{7.5 \times \sin 66^{\circ}}{8.9}\)
\(\theta\)	\(=\sin^{-1} (0.7698) \)
	\(=50.33…^{\circ} \)
	\(=50^{\circ}\ \text{(nearest degree)} \)

Trigonometry, SMB-058

Find the value of \(\theta\), correct to the nearest degree. (2 marks)

Show Answers Only

\(\theta=53^{\circ}\)

Show Worked Solution

\(\dfrac{\sin \theta}{6}\)	\(= \dfrac{\sin 37^{\circ}}{4.5} \)
\(\sin \theta\)	\(= \dfrac{6 \times \sin 37^{\circ}}{4.5}\)
\(\theta\)	\(=\sin^{-1} (0.8024) \)
	\(=53.361…^{\circ} \)
	\(=53^{\circ}\ \text{(nearest degree)} \)

Trigonometry, SMB-057

Find \(\alpha\), to the nearest degree, such that

\(\dfrac{\sin \alpha}{8} = \dfrac{\sin 60^{\circ}}{11} \) (2 marks)

Show Answers Only

\(\alpha=39^{\circ}\)

Show Worked Solution

\(\dfrac{\sin \alpha}{8}\)	\(= \dfrac{\sin 60^{\circ}}{11} \)
\(\sin \alpha\)	\(= \dfrac{8 \times \sin 60^{\circ}}{11}\)
\(\alpha\)	\(=\sin^{-1} (0.6298) \)
	\(=39^{\circ}\ \text{(nearest degree)} \)

Trigonometry, SMB-056

Find \(\theta\), to the nearest degree, such that

\(\dfrac{12}{\sin \theta} = \dfrac{15}{\sin 26^{\circ}} \) (2 marks)

Show Answers Only

\(\theta=21^{\circ}\)

Show Worked Solution

\(\dfrac{12}{\sin \theta}\)	\(= \dfrac{15}{\sin 26^{\circ}} \)
\(\dfrac{\sin \theta}{12}\)	\(= \dfrac{\sin 26^{\circ}}{15} \)
\(\sin \theta\)	\(= \dfrac{12 \times \sin 26^{\circ}}{15}\)
\(\theta\)	\(=\sin^{-1} (0.3507) \)
	\(=21^{\circ}\ \text{(nearest degree)} \)

Trigonometry, SMB-055

Find the value of \(x\), correct to 1 decimal place. (2 marks)

Show Answers Only

\(x=9.9\ \text{cm}\)

Show Worked Solution

\(\text{Angle needed}\ = 180-(115+34) = 31^{\circ}\)

\(\dfrac{x}{\sin31^{\circ}}\)	\(=\dfrac{17.5}{\sin 115^{\circ}}\)
\(x\)	\(=\dfrac{17.5 \times \sin 31^{\circ}}{\sin 115^{\circ}}\)
	\(=9.94…\)
	\(=9.9\ \text{cm (to 1 d.p.)}\)

Trigonometry, SMB-054

Find the value of \(x\), correct to 1 decimal place. (2 marks)

Show Answers Only

\(x=7.2\ \text{cm}\)

Show Worked Solution

\(\text{Angle needed}\ = 180-(81+43) = 56^{\circ}\)

\(\dfrac{x}{\sin56^{\circ}}\)	\(=\dfrac{8.6}{\sin 81^{\circ}}\)
\(x\)	\(=\dfrac{8.6 \times \sin 56^{\circ}}{\sin 81^{\circ}}\)
	\(=7.218…\)
	\(=7.2\ \text{cm (to 1 d.p.)}\)

Trigonometry, SMB-053

Find the value of \(x\), correct to 1 decimal place. (2 marks)

Show Answers Only

\(x=8.0\ \text{cm}\)

Show Worked Solution

\(\dfrac{x}{\sin42^{\circ}}\)	\(=\dfrac{12}{\sin 86^{\circ}}\)
\(x\)	\(=\dfrac{12 \times \sin 42^{\circ}}{\sin 86^{\circ}}\)
	\(=8.049…\)
	\(=8.0\ \text{cm (to 1 d.p.)}\)

Trigonometry, SMB-052

Find the value of \(x\), correct to 1 decimal place. (2 marks)

Show Answers Only

\(x=13.9\ \text{m}\)

Show Worked Solution

\(\dfrac{x}{\sin43^{\circ}}\)	\(=\dfrac{20}{\sin 78^{\circ}}\)
\(x\)	\(=\dfrac{20 \times \sin 43^{\circ}}{\sin 78^{\circ}}\)
	\(=13.944…\)
	\(=13.9\ \text{cm (to 1 d.p.)}\)

Trigonometry, SMC-051

Solve for \(b\), giving your answer correct to 1 decimal place.

\(\dfrac{b}{\sin 22^{\circ}} = \dfrac{17}{\sin 67^{\circ}}\) (2 marks)

Show Answers Only

\(b=6.9\)

Show Worked Solution

\(\dfrac{b}{\sin 22^{\circ}}\)	\(= \dfrac{17}{\sin 67^{\circ}}\)
\(b\)	\(=\dfrac{17 \times \sin 22^{\circ}}{\sin 67^{\circ}}\)
	\(=6.9\ \text{(to 1 d.p.)}\)

Trigonometry, SMB-050

Solve for \(a\), giving your answer correct to 1 decimal place.

\(\dfrac{6}{\sin 53^{\circ}} = \dfrac{a}{\sin 27^{\circ}}\) (2 marks)

Show Answers Only

\(a=3.4\)

Show Worked Solution

\(\dfrac{6}{\sin 53^{\circ}}\)	\(= \dfrac{a}{\sin 27^{\circ}}\)
\(a\)	\(=\dfrac{6 \times \sin 27^{\circ}}{\sin 53^{\circ}}\)
	\(=3.4\ \text{(to 1 d.p.)}\)

Measurement, STD2 M6 2023 HSC 35

The diagram shows triangle `ABC`.

Calculate the area of the triangle, to the nearest square metre. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`147\ text{m}^2`

Show Worked Solution

`text{Using the sine rule:}`

`(CB)/sin60^@`	`=12/sin25^@`
`CB`	`=sin60^@ xx 12/sin25^@`
	`=24.590…`

`angleACB=180-(60+25)=95^@\ \ text{(180° in Δ)}`

`text{Using the sine rule (Area):}`

`A`	`=1/2 xx AC xx CB xx sin angleACB`
	`=1/2 xx 12 xx 24.59 xx sin95^@`
	`=146.98…`
	`=147\ text{m}^2`

Measurement, STD2 M6 2022 HSC 26

The diagram shows two right-angled triangles, `ABC` and `ABD`,

where `AC=35 \ text{cm},BD=93 \ text{cm}, /_ACB=41^(@)` and `/_ADB=theta`.

Calculate the size of angle `theta`, to the nearest minute. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`19^@6^{′}`

Show Worked Solution

`text{In}\ Delta ABC:`

`cos 41^@`	`=35/(BC)`
`BC`	`=35/(cos 41^@)`
	`=46.375…`

`angle BCD = 180-41=139^@`

`text{Using sine rule in}\ Delta BCD:`

`sin theta/(46.375)`	`=sin139^@/93`
`sin theta`	`=(sin 139^@ xx 46.375)/93`
`:.theta`	`=sin^(-1)((sin 139^@ xx 46.375)/93)`
	`=19.09…`
	`=19^@6^{′}\ \ text{(nearest minute)}`

♦ Mean mark 50%.

Measurement, STD2 M6 2021 HSC 32

A right-angled triangle `XYZ` is cut out from a semicircle with centre `O`. The length of the diameter `XZ` is 16 cm and `angle YXZ` = 30°, as shown on the diagram.

Find the length of `XY` in centimetres, correct to two decimal places. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Hence, find the area of the shaded region in square centimetres, correct to one decimal place. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`13.86 \ text{cm}`
`45.1 \ text{cm}^2`

Show Worked Solution

a.	`cos 30^@`	`=(XY)/16`
	`XY`	`= 16 \ cos 30^@`
		`= 13.8564`
		`= 13.86 \ text{cm (2 d.p.)}`

b.	`text{Area of semi-circle}`	`= 1/2 times pi r^2`
		`= 1/2 pi times 8^2`
		`= 100.531 \ text{cm}^2`

♦ Mean mark part (b) 36%.

`text{Area of} \ Δ XYZ`	`= 1/2 ab\ sin C`
	`= 1/2 xx 16 xx 13.856 xx sin 30^@`
	`= 55.42 \ text{cm}^2`

`:. \ text{Shaded Area}`	`= 100.531-55.42`
	`= 45.111`
	`= 45.1 \ text{cm}^2 \ \ text{(1 d.p.)}`

Measurement, STD2 M6 2018 HSC 30c

The diagram shows two triangles.

Triangle `ABC` is right-angled, with `AB = 13 text(cm)` and `/_ABC = 62°`.

In triangle `ACD, \ AD = x\ text(cm)` and `/_DAC = 40°`. The area of triangle `ACD` is 30 cm².

What is the value of `x`, correct to one decimal place? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`8.1\ text{cm (1 d.p.)}`

Show Worked Solution

`text(Find)\ AC:`

♦ Mean mark 39%.

`sin62°`	`= (AC)/13`
`AC`	`= 13 xx sin62°`
	`= 11.478…`

`text(Using the sine rule in)\ DeltaACD :`

`text(Area)`	`= 1/2 xx AC xx AD xx sin40°`
`30`	`= 1/2 xx 11.478… xx x xx sin40°`
`:.x`	`= (30 xx 2)/(11.478… xx sin40°)`
	`= 8.13…`
	`= 8.1\ text{cm (1 d.p.)}`

Measurement, STD2 M6 2015 HSC 22 MC

The area of the triangle shown is 250 cm².

What is the value of `x`, correct to the nearest whole number?

`11`
`18`
`22`
`24`

Show Answers Only

`D`

Show Worked Solution

`text(Using)\ \ \ A = 1/2ab\ sin\ C`

♦ Mean mark 42%.

`250`	`= 1/2 xx 30x\ sin\ 44^@`
`250`	`= 15x\ sin\ 44 ^@`
`:.x`	`= 250/(15\ sin\ 44^@)`
	`= 23.99…\ text(m)`

`=>D`

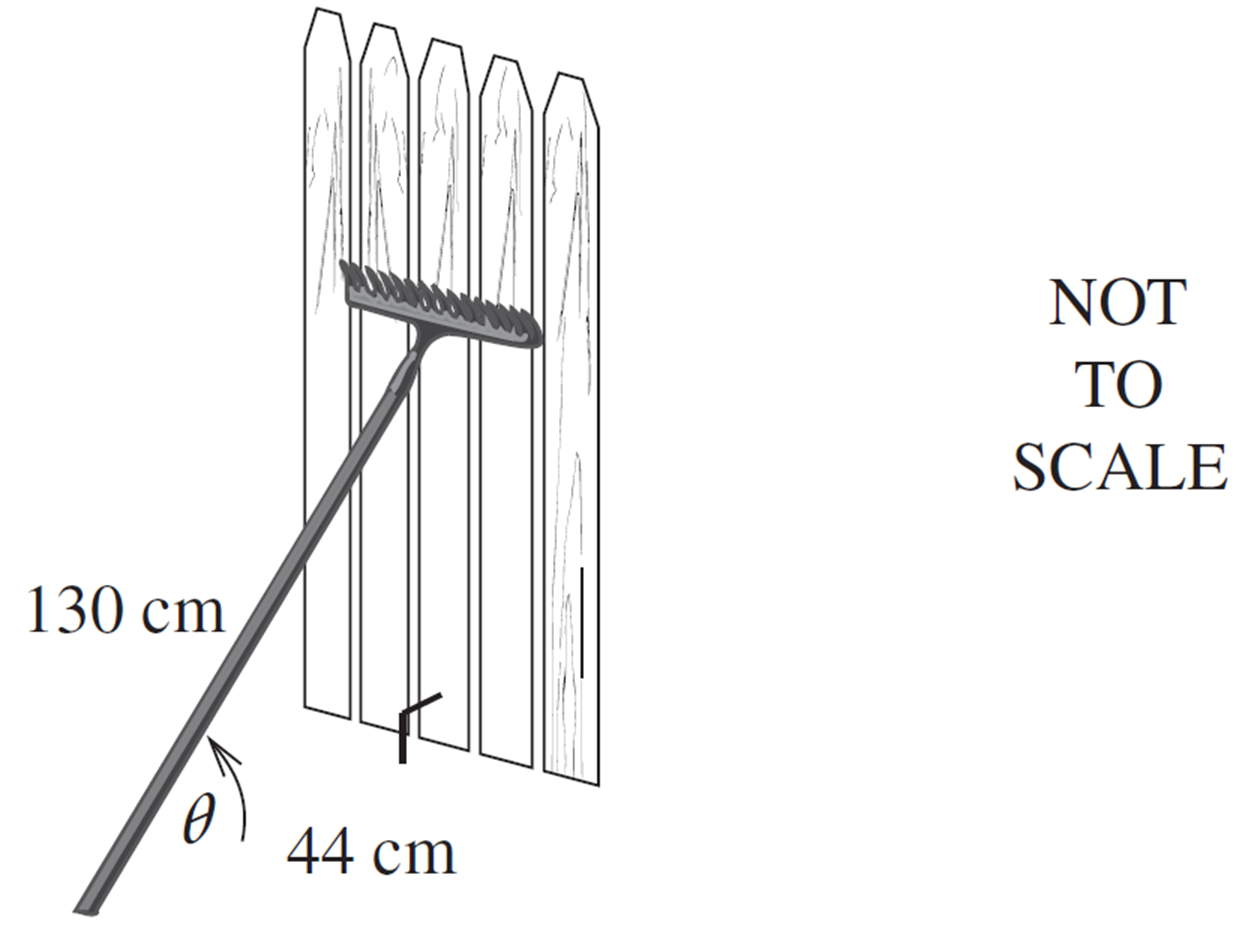
Measurement, STD2 M6 2006 HSC 24b

A 130 cm long garden rake leans against a fence. The end of the rake is 44 cm from the base of the fence.

If the fence is vertical, find the value of `theta` to the nearest degree. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The fence develops a lean and the rake is now at an angle of 53° to the ground. Calculate the new distance (`x` cm) from the base of the fence to the head of the rake. Give your answer to the nearest centimetre. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---