num-title-ct-core

Equations, SM-Bank 036

Solve the equation . (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 035

Two consecutive integers have a sum of 147.

Given the first number is , write an algebraic equation to represent this information. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Solve your equation algebraically to find the two numbers. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

b.

Equations, SM-Bank 034

Two consecutive integers have a sum of 25.

Given the first number is , write an algebraic equation to represent this information. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Solve your equation algebraically to find the two numbers. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

b.

Equations, SM-Bank 033

Find the value of in the formula if , and . (2 marks)

Show Answers Only

Show Worked Solution

Special Properties, SMB-010 MC

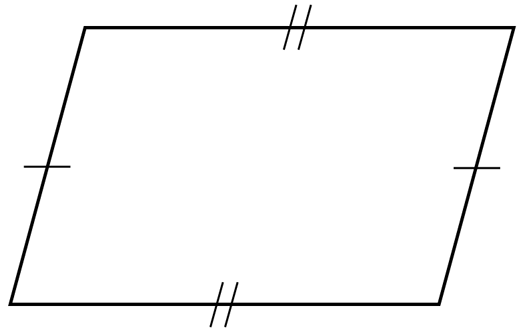
Which of these are always equal in length?

the diagonals of a rhombus
the diagonals of a parallelogram
the opposite sides of a parallelogram
the opposite sides of a trapezium

Show Answers Only

Show Worked Solution

Special Properties, SMB-009 MC

is a parallelogram.

Which of these must be a property of ?

Line is perpendicular to line .
Line is parallel to line .
Diagonals and are perpendicular.
Line is parallel to line .

Show Answers Only

Show Worked Solution

Special Properties, SMB-007 MC

A closed shape has two pairs of equal adjacent sides.

What is the shape?

rectangle
trapezium
kite
triangle

Show Answers Only

Show Worked Solution

Special Properties, SMB-004 MC

Which one of the following triangles is impossible to draw?

a right angled triangle with two acute angles
an isosceles triangle with one right angle
a scalene triangle with three acute angles
a right angled triangle with one obtuse angle

Show Answers Only

Show Worked Solution

Special Properties, SMB-002 MC

A triangle has two acute angles.

What type of angle couldn't the third angle be?

an acute angle
an obtuse angle
a right-angle
a reflex angle

Show Answers Only

Show Worked Solution

Equations, SM-Bank 032

Verify that is a solution of the equation . (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 031

Verify that is a solution of the equation . (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 030

Verify that is a solution of the equation . (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 029

Verify that is a solution of the equation . (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 028

Verify that is a solution of the equation . (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 027

Solve . (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 026

Solve . (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 025

is subtracted from a quarter of and the result is .

Write an equation and solve it algebraically to find the value of . (3 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 024

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 023

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 022

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 021

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 020

Solve (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 019

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equation, SM-Bank 018

Solve (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 017

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 016

Solve (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 015

A square with side length has an area of .

Write an equation and solve it to find the side length. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 014

A number is halved and the result is 125.6.

Write an equation and solve it to find the number. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 013

A number is tripled and the result is 141.

Write an equation and solve it to find the number. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 012

Verity and three of her friends won dollars in a lottery. When the money was divided evenly between the four friends they each received .

Write an equation and solve it to find out the total amount of their lottery winnings. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 011

Josh is currently years old. In years he will be 42.

Write an equation and solve it to find Josh's current age. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 010

Preston is paid dollars per basket of grapes he picks. Yesterday he picked baskets and he earned $306.

Write an equation and solve it to find Preston's rate of pay per basket. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 009

Missy is paid dollars per hour. Last week she worked hours and she earned $350.

Write an equation and solve it to find Missy's hourly rate of pay. (2 marks)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 008

Solve the following one-step equations.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

a.

b.

c.

d.

Equations, SM-Bank 007

Solve the following one-step equations.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

a.

b.

c.

d.

Equations, SM-Bank 006

Jace is paid dollars per hour. Last week he worked hours and he earned $300.

Write an equation describing his wages for the week. (2 marks)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 005

Marcia is years old. In years time she will be 27.

Write an equation for this description. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 004

Write an equation for:

the difference between and is . (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
the product of and is . (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
the sum of and is doubled and the answer is 8. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
half of is added to 6 and the result is 12. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Equations, SM-Bank 003

Write an equation for the sum of and is . (1 mark)

Show Answers Only

Show Worked Solution

Equations, SM-Bank 002 MC

Which of the following equations is not correct?

Show Answers Only

Show Worked Solution

Equations, SM-Bank 001 MC

Which of the following is not an equation?

Show Answers Only

Show Worked Solution

Indices, SM-Bank 103

Simplify , giving your answer in simplified index form. (2 marks)

Show Answers Only

Show Worked Solution

Indices, SM-Bank 102

Simplify , giving your answer in simplified index form. (2 marks)

Show Answers Only

Show Worked Solution

Indices, SM-Bank 101

Simplify , giving your answer in simplified index form. (2 marks)

Show Answers Only

Show Worked Solution

Indices, SM-Bank 100

Simplify , giving your answer in simplified index form. (2 marks)

Show Answers Only

Show Worked Solution

Indices, SM-Bank 099

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(2 marks)

--- 1 WORK AREA LINES (style=lined) ---
(2 marks)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 098

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(2 marks)

--- 1 WORK AREA LINES (style=lined) ---
(2 marks)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 097

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 096

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 095

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 094

Write in expanded form. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---
Write your answer to (a) in simplified index form. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 093

Write in expanded form. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---
Write your answer to (a) in simplified index form. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 092

Find the missing term in the following number sentence. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 091

Find the missing term in the following number sentence. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 090

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 089

Simplify the following, giving your answers in index form.

(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---
(1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 088

Write as a fraction in expanded form. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---
Write your answer to (a) in simplified index form. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 087

Write as a fraction in expanded form. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---
Write your answer to (a) in simplified index form. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 086

Find the missing term in the following number sentence. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Indices, SM-Bank 085

Find the missing term in the following number sentence. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution