SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Financial Maths, 2ADV M1 2024 HSC 26

Twenty-five years ago, Phoenix deposited a single sum of money into a new bank account, earning 2.4% interest per annum compounding monthly.

Present value interest factors for an annuity of $1 for various interest rates \((r)\) and numbers of periods \((n)\) are given in the table.

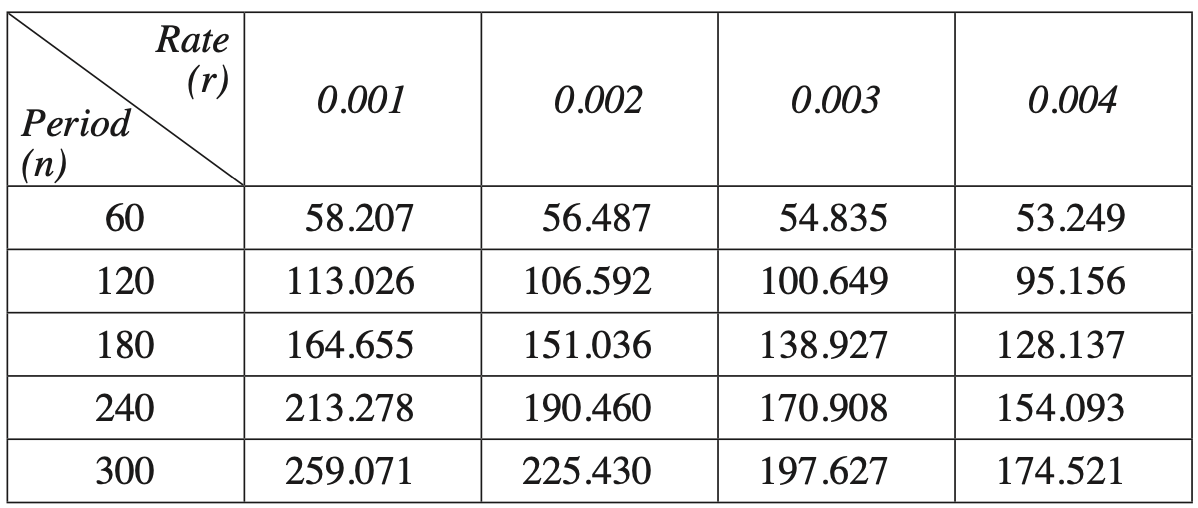
Phoenix made the following withdrawals from this account.

  • $2000 at the end of each month for the first 15 years, starting at the end of the first month.
  • $1200 at the end of each month for the next 10 years, starting at the end of the 181st month after the account was opened.

Calculate the minimum sum that Phoenix could have deposited in order to make these withdrawals.   (4 marks)

Show Answers Only

\(\text{Minimum deposit}\ = $391\,344.80\)

Show Worked Solution

\(\text{1st Annuity}\)

\(\text{Find PVA for \$2000 paid monthly for 1st 15 years:}\)

\(r= \dfrac{2.4%}{12} = 0.2\% = 0.002\)

\(\text{Total payments (to Phoenix)}\ = 15 \times 12 = 180\)

\(\text{PVA factor (from table)}\ = 151.036\)

\(\text{PVA (1st annuity)}\ = 2000 \times 151.036 = $302\,072\)

♦ Mean mark 51%.

\(\text{2nd Annuity}\)

\(\text{Find PVA for \$1200 paid monthly from year 16 to 25:}\)

\(\text{PVA (2nd annuity) = PVA (25 years) }-\text{ PVA (15 years)}\)

\(r= \dfrac{2.4%}{12} = 0.2\% = 0.002\)

\(\text{Total payments (25 years)}\ = 25 \times 12 = 300\)

\(\text{PVA factors (from table): 225.430 (25 years), 151.036 (15 years)}\)

\(\text{PVA (2nd annuity)}\) \(=(1200 \times 225.430)-(1200 \times 151.036)\)  
  \(=$89\,272.80\)  

 
\(\therefore\ \text{Minimum deposit}\ = 302\,072+89\,272.80 = $391\,344.80\)

Financial Maths, STD2 F5 2015 HSC 30c

The table gives the present value interest factors for an annuity of $1 per period, for various interest rates `(r)` and numbers of periods `(N)`.

2015 30c

  1. Oscar plans to invest $200 each month for 74 months. His investment will earn interest at the rate of 0.0080 (as a decimal) per month.

     

    Use the information in the table to calculate the present value of this annuity.  (1 mark)

  2. Lucy is using the same table to calculate the loan repayment for her car loan. Her loan is `$21\ 500` and will be repaid in equal monthly repayments over 6 years. The interest rate on her loan is 10.8% per annum.

     

    Calculate the amount of each monthly repayment, correct to the nearest dollar.  (2 marks)

Show Answers Only
  1. `$11\ 136.89\ \ text{(nearest cent)}`
  2. `$407\ \ text{(nearest dollar)}`
Show Worked Solution

i.    `N = 74, r = 0.0080`

♦ Mean mark 48%.

`PVtext{(annuity) table factor}\ = 55.68446`

`:.PV\ text(of annuity)`

`= $200 xx 55.68446`

`= $11\ 136.892`

`= $11\ 136.89\ \ text{(nearest cent)}`

 

ii.  `text(Over 6 years)`

♦♦ Mean mark 33%.

`N = 6 xx 12 = 72\ text(months)`

`r = 10.8/12 = text(0.9%) = 0.009`

`PVtext{(annuity) table factor}\ =52.82118`
 

`text(Let)\ $M =\ text(monthly repayment)`

`text(Loan)\ = PV\ text(of annuity)`

`$21\ 500` `= M xx 52.82118`
 `:.\ M` `= $407.033…`
  `= $407\ \ text{(nearest dollar)}`

Financial Maths, STD2 F5 SM-Bank 3

Camilla buys a car for $21 000 and repays it over 4 years through equal monthly instalments.

She pays a 10% deposit and interest is charged at 9% p.a. on the reducing balance loan.

Using the Table of present value interest factors below, where `r` represents the monthly interest and `N` represents the number of repayments
 

2UG FM5 S-2 

  1. Calculate the monthly repayment,  `$P`, that Camilla must pay to complete the loan after 4 years  (to the nearest $).   (3 marks)

  2. Calculate the total interest paid over the life of the loan.    (1 mark)

Show Answers Only
  1. `text(Camilla must repay $470 per month)`
  2. `$3660`
Show Worked Solution

i.  `text(Deposit) = 10text(%) xx 21\ 000 = 2100`

`text(Loan Value)` `= 21\ 000 – 2100`
  `= 18\ 900`

 
`text(Monthly interest rate) = text(9%)/12 = 0.0075`

`text(# Repayments) = 4 xx 12 = 48`

`=>\ text(PVA Factor) = 40.18478\ \ text{(from Table)}`

`text(Monthly repayment)\ ($P)` `= (18\ 900)/(40.18478)`
  `= 470.32…`
  `= 470\ text{(nearest $)}`

 
`:.\ text(Camilla must repay $470 per month.)`

 

ii.  `text(Total Repayments)`

`= 48 xx 470`

`= $22\ 560`
 

`:.\ text(Interest paid over loan)`

`= 22\ 560 – 18\ 900`

`= $3660`

Financial Maths, STD2 F5 SM-Bank 2

The table below shows the present value of an annuity with a contribution of  $1.
 

  1. Fiona pays $3000 into an annuity at the end of each year for 4 years at 2% p.a., compounded annually.   What is the present value of her annuity?  (1 mark)

  2. If John pays $6000 into an annuity at the end of each year for 2 years at 4% p.a., compounded annually, is he better off than Fiona?  Use calculations to justify your answer.    (2 marks)

Show Answers Only
  1. `$11\ 423.10`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

i.  `text(Table factor when)\ \ n = 4,\ r = text(2%) \ => \ 3.8077`

`:.\ PVA\ text{(Fiona)}` `= 3000 xx 3.8077`
  `= $11\ 423.10`

 

ii.  `text(Table factor when)\ n = 2, r = text(4%)`

`=> 1.8861`

`:.\ PVA\ text{(John)}` `= 6000 xx 1.8861`
  `= $11\ 316.60`

 
`:.\ text(Fiona will be better off because her)\ PVA`

`text(is higher.)`