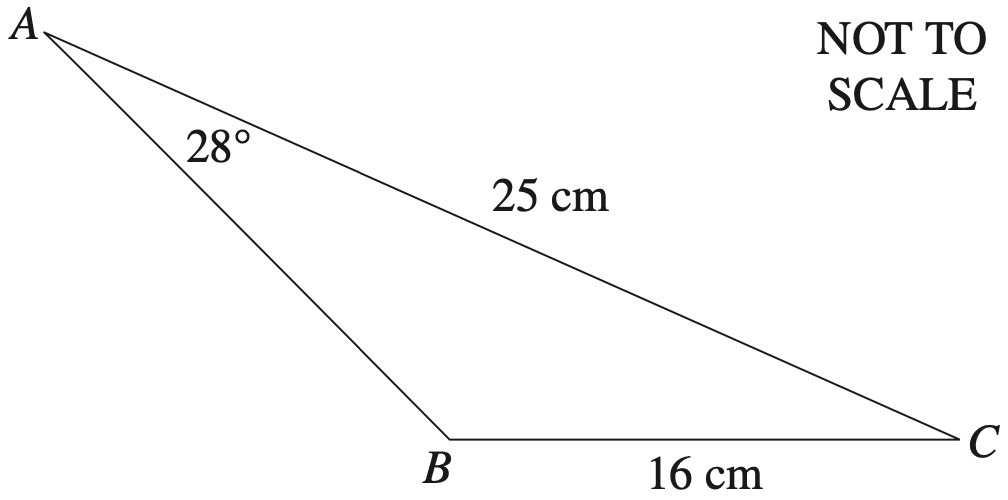
The diagram shows a shape `APQBCD`. The shape consists of a rectangle `ABCD` with an arc `PQ` on side `AB` and with side lengths `BC` = 3.6 m and `CD` = 8.0 m.
The arc `PQ` is an arc of a circle with centre `O` and radius 2.1 m and `∠POQ=110°`.
What is the perimeter of the shape `APQBCD`? Give your answer correct to one decimal place. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---