SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, EXT1 C3 2024 HSC 12b

The region, \(R\), is bounded by the function, \(y=x^3\), the \(x\)-axis and the lines  \(x=1\)  and  \(x=2\).

What is the volume of the solid of revolution obtained when the region \(R\) is rotated about the \(x\)-axis?   (3 marks)

Show Answers Only

\(V=\dfrac{127 \pi}{7} \ \ \text{u}^3\)

Show Worked Solution

  \(V\) \(=\pi \displaystyle \int_1^2 y^2\, d x\)
    \(=\pi \displaystyle \int_1^2 x^6\,d x\)
    \(=\pi\left[\dfrac{x^7}{7}\right]_1^2\)
    \(=\pi\left(\dfrac{2^7-1}{7}\right)\)
    \(=\dfrac{127 \pi}{7} \ \ \text{u}^3\)

Calculus, EXT1 C3 2022 SPEC1 10

Let `f(x)=\sec (4 x)`.

  1. Sketch the graph of `f` for `x \in\left[-\frac{\pi}{4}, \frac{\pi}{4}\right]` on the set of axes below. Label any asymptotes with their equations and label any turning points and the endpoints with their coordinates.   (3 marks)
      

      
  2. The graph of  `y=f(x)` for `x \in\left[-\frac{\pi}{24}, \frac{\pi}{48}\right]` is rotated about the `x`-axis to form a solid of revolution.
    Find the volume of this solid. Give your answer in the form `\frac{(a-\sqrt{b}) \pi}{c}`, where `a`, `b`, `c in R`.   (3 marks)
Show Answers Only

a.  
       

b.   `\frac{(3-\sqrt{3}) \pi}{6}`

Show Worked Solution

a.      
       


♦ Mean mark (a) 49%.
b.    `V` `=\pi \int_{-\frac{\pi}{24}}^{\frac{\pi}{48}} \sec ^2(4 x)\ dx`
    `=\frac{\pi}{4}[\tan (4 x)]_{-\frac{\pi}{24}}^{\frac{\pi}{48}}`
    `=\frac{\pi}{4} \tan \left(\frac{\pi}{12}\right)-\frac{\pi}{4} \tan \left(-\frac{\pi}{6}\right)`
    `=\frac{\pi}{4} \tan \left(\frac{\pi}{3}-\frac{\pi}{4}\right)-\frac{\pi}{4} \xx -\frac{1}{\sqrt{3}}`
    `=\frac{\pi}{4} \left(\frac{sqrt3-1}{1+sqrt3} xx \frac{1-sqrt3}{1-sqrt3}\right)+\frac{\pi}{4sqrt3}`
    `=\frac{\pi}{4} \left(\frac{sqrt3-3-1+sqrt3}{-2}\right)+\frac{\pi}{4sqrt3}`
    `=\frac{\pi}{4}(2-\sqrt{3}) +\frac{\pi}{4sqrt3}`
    `=\frac{\pi(2 \sqrt{3}-3+1)}{4 \sqrt{3}}`
    `=\frac{(6-2 \sqrt{3}) \pi}{12}`
    `=\frac{(3-\sqrt{3}) \pi}{6}`

♦ Mean mark (b) 55%.

Calculus, EXT1 C3 2022 HSC 13b

A solid of revolution is to be found by rotating the region bounded by the `x`-axis and the curve  `y=(k+1) \sin (k x)`, where  `k>0`, between  `x=0`  and  `x=\frac{\pi}{2 k}`  about the `x`-axis.
 

     

Find the value of `k` for which the volume is `pi^2`.  (3 marks)

Show Answers Only

`k=1`

Show Worked Solution

`y=(k+1) \sin (k x)`

`V` `=pi int_0^((pi)/(2k)) (k+1)^2sin^(2)(kx)\ dx`  
  `=pi(k+1)^2 int_0^((pi)/(2k)) 1/2[1-cos(2kx)]\ dx`  
  `=(pi/2)(k+1)^2[x-(sin(2kx))/(2k)]_0^((pi)/(2k)) `  
  `=(pi/2)(k+1)^2[(pi/(2k)- sin(pi)/(2k))-(0-sin0/(2k))]`  
  `=(pi/2)(k+1)^2(pi/(2k))`  
  `=pi^2/(4k)(k+1)^2`  

 
`text{Given}\ \ V=pi^2:`

`pi^2/(4k)(k+1)^2` `=pi^2`  
`(k+1)^2` `=4k`  
`k^2+2k+1` `=4k`  
`k^2-2k+1` `=0`  
`(k-1)^2` `=0`  

 
`:.k=1`

Calculus, EXT1 C3 2021 SPEC1 4

The shaded region in the diagram below is bounded by the graph of  `y = sin(x)`  and the `x`-axis between the first two non-negative `x`-intercepts of the curve, that is interval  `[0, pi]`.  The shaded region is rotated about the `x`-axis to form a solid of revolution.
 
       
 
Find the volume, `V_s` of the solid formed.  (3 marks)

Show Answers Only

`(pi^2)/2\ text(u)³`

Show Worked Solution
  `V_s` `= pi int_0^pi sin^2(x)\ dx`
    `= pi int_0^pi 1/2(1 – cos(2x))\ dx`
    `= pi/2 int_0^pi 1 – cos(2x)\ dx`
    `= pi/2 [x – 1/2 sin(2x)]_0^pi`
    `= pi/2[pi – 1/2 sin(2pi) – (0 – 1/2 sin 0)]`
    `= (pi^2)/2\ text(u)³`

Calculus, EXT1 C3 2020 HSC 13b

The region `R` is bounded by the `y`-axis, the graph of  `y = cos(2x)`  and the graph of  `y = sin x`, as shown in the diagram.
 

Find the volume of the solid of revolution formed when the region `R` is rotated about the `x`-axis.  (4 marks)

Show Answers Only

`(3sqrt3 pi)/16\ text(u)³`

Show Worked Solution

`text(Find intersection:)`

Mean mark 53%.

`sin x = cos 2x`

`sin x = 1 – 2sin^2 x`

`2sin^2 x + sinx – 1` `= 0`
`(2 sinx – 1)(sinx + 1)` `= 0`
`sin x` `= 1/2` `text(or)` `sin x` `= −1`
`x` `= pi/6`   `x` `= (3pi)/2`

 

`V` `= pi int_0^(pi/6) (cos 2x)^2\ dx – pi int_0^(pi/6)(sin x)^2\ dx`
  `= pi int_0^(pi/6) cos^2 2x – sin^2 x\ dx`
  `= pi int_0^(pi/6) 1/2 (1 + cos 4x) – 1/2 (1 – cos 2x)\ dx`
  `= pi/2 int_0^(pi/6) cos 4x + cos 2x\ dx`
  `= pi/2 [1/4 sin 4x + 1/2 sin 2x]_0^(pi/6)`
  `= pi/8 [sin\ (2pi)/3 + 2sin\ pi/3]`
  `= pi/8 (sqrt3/2 + 2 xx sqrt3/2)`
  `= (3sqrt3 pi)/16\ text(u)³`

Calculus, EXT1 C3 SM-Bank 3

Find the volume of the solid of revolution formed when the graph of  `y = sqrt((1 + 2x)/(1 + x^2))`  is rotated about the `x`-axis over the interval  `[0,1]`.  (3 marks)

Show Answers Only

`pi(pi/4 + ln2)\ \ text(u³)`

Show Worked Solution
`V` `= pi int_0^1 (1 + 2x)/(1 + x^2)\ dx`
  `= pi int_0^1 1/(1 + x^2)\ dx + pi int_0^1 (2x)/(1 + x^2)\ dx`
  `= pi [tan^(−1)(x)]_0^1 + pi [ln(1 + x^2)]_0^1`
  `= pi(tan^(−1)1 – tan^(−1)0) + pi(ln2 – ln1)`
  `= pi(pi/4) + pi(ln2)`
  `= pi(pi/4 + ln2)\ \ text(u³)`

Calculus, EXT1* C3 2019 HSC 13d

The diagram shows the region bounded by the curve  `y = x - x^3`, and the `x`-axis between  `x = 0`  and  `x = 1`. The region is rotated about the `x`-axis to form a solid.
 


 

Find the exact value of the volume of the solid formed.  (3 marks)

Show Answers Only

`(8 pi)/105\ text(u³)`

Show Worked Solution
`V` `= pi int_0^1 (x – x^3)^2 dx`
  `= pi int_0^1 x^2 – 2x^4 + x^6\ dx`
  `= pi [x^3/3 – 2/5 x^5 + 1/7 x^7]_0^1`
  `= pi(1/3 – 2/5 + 1/7)`
  `= (8 pi)/105\ text(u³)`

Calculus, EXT1 C3 SM-Bank 1

The region enclosed by the semicircle  `y = sqrt(1 - x^2)`  and the `x`-axis is to be divided into two pieces by the line  `x = h`, when  `0 <= h <1`.
 


 

The two pieces are rotated about the `x`-axis to form solids of revolution. The value of `h` is chosen so that the volumes of the solids are in the ratio `2 : 1`.

Show that `h` satisfies the equation  `3h^3 - 9h + 2 = 0`.  (3 marks)

Show Answers Only

`text(Show Worked Solution)`

Show Worked Solution

(i)   `text(Volume of smaller solid)`

`= pi int_h^1 (sqrt(1 – x^2))^2\ dx`

`= pi int_h^1 1 – x^2\ dx`

`= pi[x – (x^3)/3]_h^1`

`= pi[(1 – 1/3) – (h – (h^3)/3)]`

`= pi(2/3 – h + (h^3)/3)`

 
`text(S)text(ince smaller solid is)\ 1/3\ text(volume of sphere,)`

`pi(2/3 – h + (h^3)/3)` `= 1/3 xx 4/3 · pi · 1^3`
`(h^3)/3 – h + 2/3` `= 4/9`
`3h^3 – 9h + 6` `= 4`
`:. 3h^3 – 9h + 2` `= 0\ \ text(… as required)`

Calculus, EXT1* C3 2017 HSC 12b

The diagram shows the region bounded by  `y = sqrt (16 - 4x^2)`  and the `x`-axis.
 


 

The region is rotated about the `x`-axis to form a solid.

Find the exact volume of the solid formed.  (3 marks)

Show Answers Only

`(128 pi)/3\ text(u³)`

Show Worked Solution
`y` `= sqrt (16 – 4x^2)`
`V` `= pi int_(-2)^2 y^2\ dx`
  `= 2 pi int_0^2 16 – 4x^2\ dx`
  `= 2 pi [16x – 4/3 x^3]_0^2`
  `= 2 pi [(16 ⋅ 2 – 4/3 2^3)-0]`
  `= 2 pi (64/3)`
  `= (128 pi)/3\ text(u³)`

Calculus, EXT1* C3 2016 HSC 15a

The diagram shows two curves  `C_1` and `C_2.` The curve `C_1` is the semicircle  `x^2 + y^2 = 4, \ -2 <= x <= 0.` The curve `C_2` has equation  `x^2/9 + y^2/4 = 1, \ 0 <= x <= 3.`
 

hsc-2016-15a
 

An egg is modelled by rotating the curves about the `x`-axis to form a solid of revolution.

Find the exact value of the volume of the solid of revolution.  (4 marks)

Show Answers Only

`(40 pi)/3\ text(u³)`

Show Worked Solution

`text(Consider)\ \ C_1,`

`V_1` `= pi int_-2^0 y^2\ dx`
  `= pi int_-2^0 4 – x^2\ dx`
  `= pi [4x – x^3/3]_-2^0`
  `= pi [0 – (-8 + 8/3)]`
  `= (16 pi)/3\ u³`

 

`text(Consider)\ \ C_2`

`x^2/9 + y^2/4` `= 1`
`y^2` `= 4 – (4x^2)/9`

 

`V_2` `= pi int_0^3 4 – (4x^2)/9\ dx`
  `= pi [4x – (4x^3)/27]_0^3`
  `= pi [(12 – (4 · 3^3)/27) – 0]`
  `= 8 pi\ text(u³)`

 

`text(Volume)` `= V_1 + V_2`
  `= (16 pi)/3 + 8 pi`
  `= (40 pi)/3\ text(u³)`

Calculus, EXT1* C3 2004 HSC 4c

2004 4c

In the diagram, the shaded region is bounded by the curve  `y = 2 sec x`, the coordinate axes and the line  `x = pi/3`. The shaded region is rotated about the `x`-axis.

Calculate the exact volume of the solid of revolution formed.  (3 marks)

Show Answers Only

`4sqrt3\ pi\ \ text(u³)`

Show Worked Solution
`y` `= 2 sec x`
`:. y^2` `= 4 sec^2 x`

 

`V` `= pi int_0^(pi/3) y^2\ dx`
  `= pi int_0^(pi/3) 4 sec^2 x\ dx`
  `= 4pi int_0^(pi/3) sec^2 x\ dx`
  `= 4pi[tan x]_0^(pi/3)`
  `= 4pi(tan\ pi/3 − tan 0)`
  `= 4pi(sqrt3 − 0)`
  `= 4sqrt3\ pi\ \ text(u³)`

Calculus, EXT1* C3 2007 HSC 3a

Find the volume of the solid of revolution formed when the region bounded by the curve  `y = 1/(sqrt(9 + x^2))`, the `x`-axis, the `y`-axis and the line  `x = 3`, is rotated about the `x`-axis.  (3 marks)

Show Answers Only

`(pi^2)/(12)\ \ text(u³)`

Show Worked Solution

`y = 1/(sqrt(9 + x^2))`

`:.\ text(Volume)` `= pi int_0^3 y^2\ dx`
  `= pi int_0^3 (1/(sqrt(9 + x^2)))^2\ dx`
  `= pi int_0^3 1/(9 + x^2)\ dx`
  `= pi [1/3 tan^(−1)\ x/3]_0^3`
  `= pi [1/3 tan^(−1)\ 1 − 1/3 tan^(−1)\ 0]`
  `= pi [(1/3 xx pi/4) − 0]`
  `= (pi^2)/(12)\ \ text(u³)`

Calculus, EXT1 C3 2005 HSC 5a

Find the exact value of the volume of the solid of revolution formed when the region bounded by the curve  `y = sin 2x`, the `x`-axis and the line  `x = pi/8`  is rotated about the `x`-axis.  (3 marks)

Show Answers Only

`pi/16 (pi – 2)\ \ \ text(u³)`

Show Worked Solution
`y` `= sin 2x`
`y^2` `= sin^2 2x` 

 
`text(Using:)\ \ sin^2 x= 1/2 (1 – cos 2x)`

COMMENT: Michael Wells (1st in state Ext2) would derive this formula in his working from the `sin^2x+cos^2=1` identity in ~5 seconds every time he used it in an exam.
  

`:. V` `=pi int_0^(pi/8) y^2 \ dx`
  `= pi int_0^(pi/8) sin^2 2x \ dx`
  `= pi/2 int_0^(pi/8) 1 – cos\ 4x\ dx`
  `= pi/2 [x – 1/4 sin\ 4x]_0^(pi/8)`
  `= pi/2 [(pi/8 – 1/4 sin\ pi/2) – 0]`
  `= pi/2 (pi/8 – 1/4)`
  `= pi/2 ((pi – 2)/8)`
  `= pi/16 (pi – 2)\ \ \ text(u³)`

Calculus, EXT1* C3 2007 HSC 9a

2007 9a
  

The shaded region in the diagram is bounded by the curve  `y = x^2 + 1`, the `x`-axis, and the lines  `x = 0`  and  `x = 1.`

Find the volume of the solid of revolution formed when the shaded region is rotated about the `x`-axis.  (3 marks)

Show Answers Only

`(28 pi)/15\ \ text(u³)`

Show Worked Solution
`V` `= pi int_0^1 y^2\ dx`
  `= pi int_0^1 (x^2 + 1)^2\ dx`
  `= pi int_0^1 x^4 + 2x^2 + 1\ dx`
  `= pi [1/5 x^5 + 2/3 x^3 + x]_0^1`
  `= pi[(1/5 + 2/3 + 1) – 0]`
  `= pi [3/15 + 10/15 + 1]`
  `= (28 pi)/15\ \ text(u³)`

Calculus, EXT1* C3 2008 HSC 6c

The graph of  `y = 5/(x - 2)`  is shown below.
 

2008 6c
 

The shaded region in the diagram is bounded by the curve  `y = 5/(x - 2)`, the  `x`-axis and the lines  `x = 3`  and  `x = 6`.

Find the volume of the solid of revolution formed when the shaded region is rotated about the  `x`-axis.  (3 marks)

Show Answers Only

`(75pi)/4\ text(u³)`

Show Worked Solution
`y` `= 5/(x – 2)`
`V` `= pi int_3^6 y^2\ dx`
  `= pi int_3^6 (5/(x – 2))^2\ dx`
  `= 25 pi int_3^6 1/((x – 2)^2)\ dx`
  `= 25 pi [(-1)/(x – 2)]_3^6`
  `= 25 pi [-1/4 – (-1)]`
  `=25 pi [3/4]`
  `= (75pi)/4\ text(u³)`

Calculus, EXT1 C3 2014 HSC 12b

The region bounded by  `y = cos 4x`  and the  `x`-axis, between  `x = 0`  and  `x = pi/8`, is rotated about the  `x`-axis to form a solid.   
 

2014 12b
 

Find the volume of the solid.   (3 marks)

Show Answers Only

`(pi^2)/16\ \ text(u³)`

Show Worked Solution
COMMENT: The identities `cos 2theta=` `cos^2 theta-sin^2 theta =` ` 2cos^2 theta-1=1-2sin^2 theta`  are tested every year – know them. 
`V` `= pi int_0^(pi/8) y^2\ dx`
  `= pi int_0^(pi/8) cos^2 4x\ dx`
  `= pi int_0^(pi/8) 1/2 (cos 8x + 1)\ dx`
  `= pi/2 [1/8 sin 8x + x]_0^(pi/8)`
  `= pi/2 [(1/8 sin pi + pi/8)] – 0]`
  `= (pi^2)/16\ \ text(u³)`

Calculus, EXT1* C3 2014 HSC 14c

The region bounded by the curve  `y = 1 + sqrtx`  and the  `x`-axis between  `x = 0`  and  `x = 4`  is rotated about the  `x`-axis to form a solid.
 

2014 14c
 

Find the volume of the solid.   (3 marks) 

Show Answers Only

`(68 pi)/3\ text(u³)`

Show Worked Solution

`y = 1 + sqrtx`

`V` `= pi int_0^4 y^2\ dx`
  `= pi int_0^4 (1 + sqrtx)^2\ dx`
  `= pi int_0^4 (1 + 2 sqrtx + x)\ dx`
  `= pi [x + 4/3 x^(3/2) + 1/2 x^2]_0^4`
  `= pi [(4 + 4/3 xx 4^(3/2) + 1/2 xx 4^2)\ – 0]`
  `= pi (4 + 32/3 + 8)`
  `= (68 pi)/3\ text(u³)`

Calculus, EXT1 C3 2013 HSC 12b

The region bounded by the graph  `y = 3 sin\ x/2`  and the  `x`-axis between  `x = 0`  and  `x = (3pi)/2`  is rotated about the  `x`-axis to form a solid.  
 

2013 12b
 

Find the exact volume of the solid.   (3 marks)

Show Answers Only

`(9pi)/2 ((3pi)/2 + 1) text(u³)`

Show Worked Solution
`y` `= 3 sin\ x/2`
`y^2` `= 9 sin^2\ x/2`

 
`text(Using:)\ \ sin^2x= 1/2 (1 – cos 2x)`
 

`:. V` `= pi int_0^((3pi)/2) 9 sin^2\ x/2\ dx`
  `= (9pi)/2 int_0^((3pi)/2) (1\ – cosx)\ dx`
  `= (9pi)/2 [x\ – sinx]_0^((3pi)/2)`
  `= (9pi)/2 [((3pi)/2\ – sin\ (3pi)/2)\ – 0]`
  `= (9pi)/2 ((3pi)/2 + 1)\ text(u³)`

Calculus, EXT1* C3 2009 HSC 6a

The diagram shows the region bounded by the curve  `y = sec x`, the lines  `x = pi/3`  and  `x = -pi/3`,  and the  `x`-axis. 
 

2009 6a
 

The region is rotated about the   `x`-axis. Find the volume of the solid of revolution formed.   (3 marks)

Show Answers Only

 `2 sqrt 3 pi\ text(u³)`

Show Worked Solution
`V` `= pi int_(-pi/3)^(pi/3) y^2\ dx`
  `= pi int_(-pi/3)^(pi/3) sec^2x\ dx`
  `= pi [tanx]_(-pi/3)^(pi/3)`
  `= pi[tan(pi/3) – tan(-pi/3)]`
  `= pi [sqrt3\ – (-sqrt3)]`
  `= 2 sqrt3 pi\ text(u³)`

Calculus, EXT1* C3 2010 HSC 10b

The circle  `x^2 + y^2 = r^2`  has radius `r` and centre `O`. The circle meets the positive `x`-axis at `B`. The point `A` is on the interval `OB`. A vertical line through `A` meets the circle at `P`. Let  `theta = /_OPA`.
  

2010 10b1

  1. The shaded region bounded by the arc `PB` and the intervals `AB` and `AP` is rotated about the `x`-axis. Show that the volume, `V`, formed is given by
  2. `V = (pi r^3)/3 (2-3 sin theta + sin^3 theta)`   (3 marks)

  3. A container is in the shape of a hemisphere of radius `r` metres. The container is initially horizontal and full of water. The container is then tilted at an angle of `theta` to the horizontal so that some water spills out. 

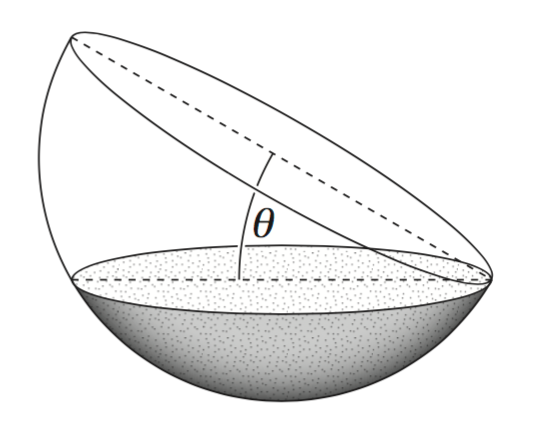
  1. (1) Find `theta` so that the depth of water remaining is one half of the original depth.   (1 mark)

  2. (2) What fraction of the original volume is left in the container?   (2 marks)

Show Answers Only
  1. `text(Proof)  text{(See Worked Solutions)}`
  2. (1) `theta = pi/6\ text(radians)`
  3. (2) `5/16`
Show Worked Solution

i.    `text(Show that)\ V = (pir^3)/3 (2-3sin theta + sin^3 theta)`

♦♦♦ Mean mark (i) 16%.
MARKER’S COMMENT: A common error was to integrate `r^2` to `1/3 r^3` instead of `r^2 x` (note that `r` is a constant).  
`sin theta` `= (OA)/r`
`:.\ OA` `= r sin theta`
`=> A` `= (r sin theta, 0),\ \ \ \ B = (r,0)`

 

`:.V` `= pi int_(rsintheta)^r y^2\ dx`
  `= pi int_(rsintheta)^r (r^2-x^2)\ dx\ \ \ \ text{(using}\ x^2+y^2=r^2text{)}`
  `= pi [r^2 x-(x^3)/3]_(rsintheta)^r`
  `= pi [(r^3-r^3/3)-(r^3 sin theta-(r^3 sin^3 theta)/3)]`
  `= pi ((2r^3)/3-r^3 sin theta + (r^3 sin^3 theta)/3)`
  `= (pir^3)/3 (2-3 sin theta + sin^3 theta)\ \ \ text(… as required)`

 

ii. (1) `text(Depth of water remaining) = 1/2 xx text(original depth:)`

♦♦♦ Part (ii) mean marks 3% and 2% for (ii)(1) and (ii)(2) respectively.
`r-r sin theta` `=1/2 r`
`r (1-sin theta)` `= 1/2 r`
`1-sin theta` `= 1/2`
`sin theta` `= 1/2`
`:.\ theta` `= pi/6\ text(radians)`

 

 MARKER’S COMMENT: Previous parts of a question should always be at the front and centre of a student’s mind and direct their strategy.
ii. (2)    `text(Original Volume)` `= 1/2 xx 4/3 pi r^3`
    `= 2/3 pi r^3`

 

`text(New Volume)` `= (pi r^3)/3 [2-3 sin(pi/6) + sin^3(pi/6)]`
  `= (pir^3)/3 [2-(3 xx 1/2) + (1/2)^3]`
  `= (pi r^3)/3 [2-3/2 + 1/8]`
  `= (pir^3)/3 (5/8)`
  `= (5 pi r^3)/24`

 

`:.\ text(Fraction of original volume left)`

`= ((5pir^3)/24)/(2/3 pi r^3)`

`= 5/24 xx 3/2`

`= 5/16`

Calculus, EXT1* C3 2012 HSC 14b

The diagram shows the region bounded by  `y = 3/((x+2)^2)`, the `x`-axis, the  `y`-axis,  and the line  `x = 1`.  
 

2012 14b
 

The region is rotated about the  `x`-axis to form a solid.

Find the volume of the solid.  (3 marks)

Show Answers Only

 `(19pi)/72\ text(u³)`

Show Worked Solution
MARKER’S COMMENT: Most students omitted the `dx` when stating the definite integral in this question!
`V` `= pi int_0^1 y^2\ dx`
  `= pi int_0^1 (3/((x+2)^2))^2\ dx`
  `= pi int_0^1 9/((x+2)^4)\ dx`
  `= 9pi int_0^1 (x + 2)^-4\ dx`
  `= 9pi  [-1/3 (x + 2)^-3]_0^1`
  `= 9pi  [(-1/3 xx 1/(3^3))\ – (-1/3 xx 1/(2^3))]`
  `= 9 pi [-1/81 + 1/24]`
  `= 9 pi (19/648)`
  `= (19pi)/72\ text(u³)`

 

`:.\ text(Volume of the solid is)\ (19pi)/72\ text(u³)`.