SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, EXT1 C1 2020 HSC 10 MC

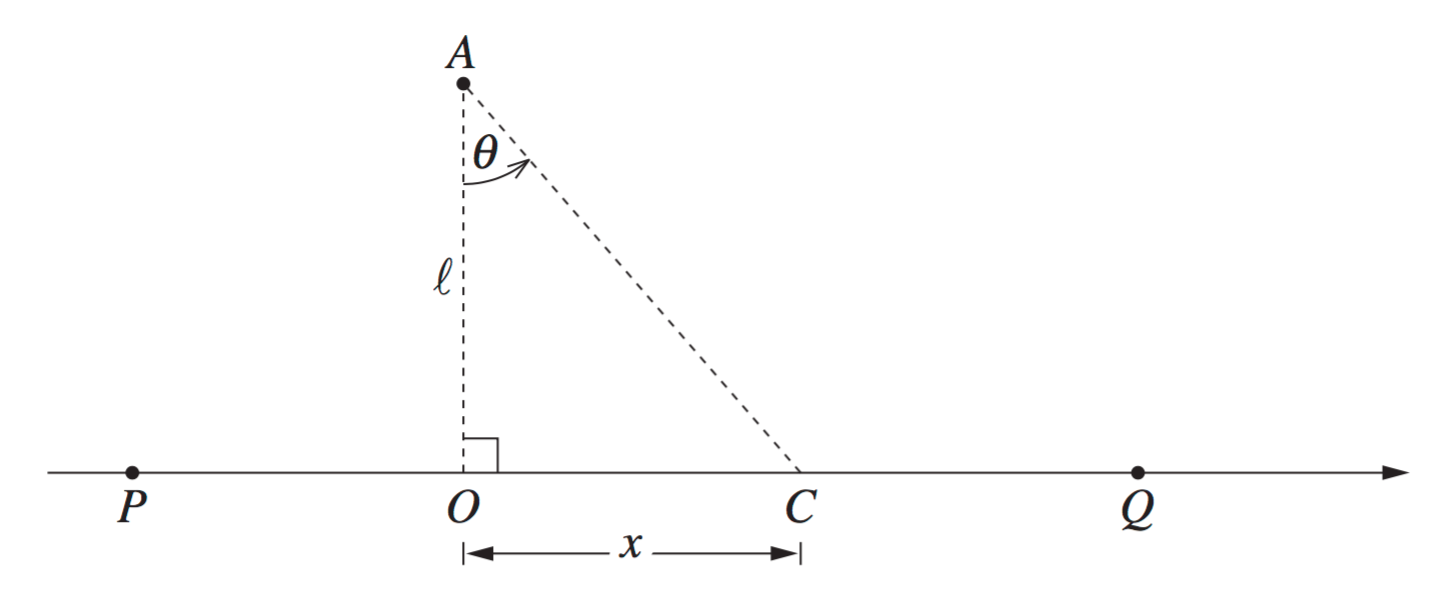
The quantities `P`, `Q` and `R` are connected by the related rates.

`(dR)/(dt) = −k^2`

`(dP)/(dt) = −l^2 xx (dR)/(dt)`

`(dP)/(dt) = m^2 xx (dQ)/(dt)`

where `k`, `l` and `m` are non-zero constants.

Which of the following statements is true?

  1. `P` is increasing and `Q` is increasing
  2. `P` is increasing and `Q` is decreasing
  3. `P` is decreasing and `Q` is increasing
  4. `P` is decreasing and `Q` is decreasing
Show Answers Only

`A`

Show Worked Solution

`(dR)/(dt) = −k^2 < 0 => R\ text(is decreasing)`

`(dP)/(dt) = −l^2 xx (dR)/(dt) > 0 => P\ text(is increasing)`

`(dP)/(dt) = m^2 xx (dQ)/(dt) > 0 => Q\ text(is increasing)`

`=> A`

Calculus, EXT1 C1 2019 HSC 12a

Distance `A` is inversely proportional to distance `B`, such that  `A = 9/B`  where `A` and `B` are measured in metres. The two distances vary with respect to time. Distance `B` is increasing at a rate of  `0.2\ text(ms)^(-1)`.

What is the value of  `(dA)/(dt)`  when  `A = 12`?  (3 marks)

Show Answers Only

`-3.2\ text(ms)^(-1)`

Show Worked Solution

`A = 9/B,\ \ (dB)/(dt) = 0.2\ \ text{(given)}`

`(dA)/(dB)` `= -9/B^2`
`(dA)/(dt)` `= (dA)/(dB) xx (dB)/(dt)`
  `= -9/B^2 xx 0.2`

 
`text(When)\ \ A = 12\ \ =>\ \ B = 3/4 :`

`(dA)/(dt)` `= -9/(3/4)^2 xx 0.2`
  `= -3.2\ text(ms)^(-1)`

Calculus, EXT1 C1 2018 HSC 12b

A ferris wheel has a radius of 20 metres and is rotating at a rate of 1.5 radians per minute. The top of a carriage is `h` metres above the horizontal diameter of the ferris wheel. The angle of elevation of the top of the carriage from the centre of the ferris wheel is `theta`.
 


 

  1. Show that  `(dh)/(d theta) = 20 cos theta`.  (1 mark)

  2. At what speed is the top of the carriage rising when it is 15 metres higher than the horizontal diameter of the ferris wheel? Give your answer correct to one decimal place.  (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solution)}`
  2. `19.8\ text{metres per minute  (1 d.p)}`
Show Worked Solution

i.   `text(From the diagram,)`

`sin theta` `= h/20`
`h` `= 20 sin theta`
`:. (dh)/(d theta)` `= 20 cos theta`

 

ii.   `text(Find)\ \ (dh)/(dt)\ text(when)\ h = 15:`

`(dh)/(dt)` `= (dh)/(d theta) xx (d theta)/(dt)`
  `= (20 cos theta) xx 1.5`
  `= 30 cos theta`

 
`text(Find)\ cos theta\ \ text(when)\ h = 15`

`text(Using Pythagoras,)`

`cos theta` `=sqrt(20^2 – 15^2)/20`  
  `=sqrt7/4`  

 

`:. (dh)/(dt)` `= 30 cos theta`
  `= (15 sqrt 7)/2`
  `~~ 19.8\ text{metres per minute  (1 d.p)}`

Calculus, EXT1 C1 2005 HSC 7a

An oil tanker at  `T`  is leaking oil which forms a circular oil slick. An observer is measuring the oil slick from a position  `P`, 450 metres above sea level and 2 kilometres horizontally from the centre of the oil slick.
 


 

  1. At a certain time the observer measures the angle, `alpha`, subtended by the diameter of the oil slick, to be 0.1 radians. What is the radius, `r`, at this time?  (2 marks)

  2. At this time, `(d alpha)/(dt) = 0.02`  radians per hour. Find the rate at which the radius of the oil slick is growing.  (2 marks)

Show Answers Only
  1. `102.6\ text{m  (to 1 d.p.)}`
  2. `20.6\ text{metres  (to 1 d.p.)}`
Show Worked Solution

i.

`text(Let)\ \ Q\ \ text(be the point on the sea such)\ \ /_PQT`

`text(is a right angle.)`

 
`text(Consider)\ \ Delta PQT,`

`text(Using Pythagoras,)`

`PT^2` `= PQ^2 + QT^2`
  `= 450^2 + 2000^2`
`PT` `= sqrt(450^2 + 2000^2)`
  `= 2050\ text(m)`

 
`text(Consider)\ \ Delta PMT`

`tan\  /_ MPT` `= r/(PT)`
`tan 0.05` `= r/2050`
`:. r` `= 2050 xx tan 0.05`
  `= 102.585…`
  `= 102.6\ text{m  (to 1 d.p.)}`

 

ii.  `text(Find)\ \ (dr)/(dt)\ \ text(when)\ \ alpha = 0.1`

`(dr)/(dt)` `= (dr)/(d alpha) * (d alpha)/(dt)`
   
`r` `= 2050 xx tan\ alpha/2`
`:.\ (dr)/(d alpha)` `= 2050 xx 1/2 xx sec^2\ alpha/2`
  `= 1025 sec^2\ alpha/2`

  
`text(When)\ \ (d alpha)/(dt)= 0.02\ \ text(radians per hour),`

`alpha = 0.1\ \ \ text{(given)}.`

`:. (dr)/(dt)` `= 1025 sec^2 0.05 xx 0.02`
  `= 20.5513…`
  `= 20.6\ text{metres per hour  (to 1 d.p.)}`

Calculus, EXT1 C1 2008 HSC 3c

2008 3c
  
 A race car is travelling on the  `x`-axis from  `P`  to  `Q`  at a constant velocity,  `v`.

A spectator is at  `A`  which is directly opposite  `O`, and  `OA = l`  metres. When the car is at  `C`, its displacement from  `O`  is  `x`  metres and  `/_OAC = theta`, with  `- pi/2 < theta < pi/2`.

  1. Show that  `(d theta)/(dt) = (vl)/(l^2 + x^2)`.   (2 marks)

  2. Let  `m`  be the maximum value of  `(d theta)/dt`.  

     

    Find the value of  `m`  in terms of  `v`  and  `l`.   (1 mark)

  3. There are two values of  `theta`  for which  `(d theta)/(dt) = m/4`.

     

    Find these two values of  `theta`.   (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `v/l`
  3. `+- pi/3`
Show Worked Solution

i.  `text(Show)\ \ (d theta)/(dt) = (vl)/(l^2 + x^2)`

`(d theta)/(dt)` `= (d theta)/(dx) * (dx)/(dt)\ \ \ \ \ \ \ …\ (1)`
`v` `= (dx)/(dt)\ \ \ text{(given)}`

 

`text(Find)\ \ (d theta)/(dx),`

MARKER’S COMMENT: The most successful students used  `theta=tan^-1(x/l)` and the chain rule to find `(d theta)/(dt)`.
`tan theta` `= x/l`
`theta` `= tan^-1 (x/l)`
`(d theta)/(dx)` `= l/(l^2+x^2)`
 
`text{Substituting into (1),}`
`(d theta)/(dt)` `= l/(l^2+x^2) * v`
  `= (vl)/(l^2 + x^2)\ \ \ text(… as required)`

 

ii.  `(d theta)/(dt)\ \ text(is a MAX when)\ \ x = 0`

`:. m` `= (vl)/(l^2 + 0^2)`
  `= v/l`

 

iii.  `text(Find)\ \ theta\ \ text(when)\ \ (d theta)/(dt) = m/4`

MARKER’S COMMENT: Many students lost marks by not giving their answer in the specified range. Be careful!
`=> (d theta)/(dt)` `= v/(4l)`
`(vl)/(l^2 +x^2)` `= v/(4l)`
`l^2 + x^2` `= 4l^2`
`x^2` `= 3l^2`
`x` `= +- sqrt3 l`

 

`tan theta` `= x/l`
  `= +- sqrt 3`
`:. theta` `= +- pi/3,\ \ \ \ \ (- pi/2 < theta < pi/2)`

Calculus, EXT1 C1 2012 HSC 14c

A plane `P` takes off from a point `B`. It flies due north at a constant angle `alpha` to the horizontal. An observer is located at `A`, 1 km from `B`, at a bearing 060° from `B`.

Let `u` km be the distance from `B` to the plane and let `r` km be the distance from the observer to the plane. The point `G` is on the ground directly below the plane.
 

2012 14c
 

  1. Show that  `r = sqrt(1 + u^2 - u cos alpha)`.   (3 marks)

  2. The plane is travelling at a constant speed of 360 km/h.
  3. At what rate, in terms of  `alpha`, is the distance of the plane from the observer changing 5 minutes after take-off?    (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `(180 (60\ – cos alpha))/sqrt(901\ – 30 cos alpha)\ \ text(km/hr)`
Show Worked Solution

i.  `text(Show)\ r = sqrt(1 + u^2 – u cos alpha)`

♦ Mean mark 42%
IMPORTANT: Students should always be looking for opportunities to use the identity `sin^2 alpha“+cos^2 alpha=1` to clean up calculations with trig functions.

`text(In)\ Delta PGB:`

`cos alpha` `= (BG)/u`
`BG` `= u cos alpha`
`sin alpha` `= (PG)/(u)`
`PG` `= u sin alpha`

 
`text(In)\ Delta PGA,\ text(using Pythagoras):`

`AG^2` `= r^2\ – PG^2`
  `= r^2\ – u^2 sin^2 alpha`

 
`text(Using cosine rule in)\ Delta ABG:`

`AG^2` `= BG^2 + AB^2\ – 2 xx BG xx AB xx cos 60^@`
`r^2\ – u^2 sin^2 alpha` `= u^2 cos^2 alpha + 1\ – 2 (u cos alpha) xx 1 xx 1/2`
`r^2` `= u^2 cos^2 alpha + u^2 sin^2 alpha + 1\ – u cos alpha`
  `= u^2 (cos^2 alpha + sin^2 alpha) + 1\ – u cos alpha`
  `= u^2 + 1\ – u cos alpha`
`r` `= sqrt(u^2 + 1\ – u cos alpha)\ \ text(… as required)`

 

ii.  `text(Find)\ \ (dr)/(dt)\ text(when)\ t =5`

♦♦♦ Mean mark 14%

`(dr)/(dt) = (dr)/(du) xx (du)/(dt)`

`r` `= (u^2 + 1\ – u cos alpha)^(1/2)`
`(dr)/(du)` `= 1/2 (u^2 + 1\ – u cos alpha)^(-1/2) xx (2u\ – cos alpha)`
  `= (2u\ – cos alpha)/(2 sqrt(u^2 + 1\ – u cos alpha))`

 
`(du)/(dt)= 360\ text{km/hr   (plane’s speed)}`

 
`text(After 5 mins,)`

`u` `= 5/60 xx 360 = 30\ text(km)`
`(dr)/(dt)` `= ((2 xx 30)\ – cos alpha)/( 2 sqrt(30^2 + 1\ – 30 cos alpha)) xx 360`
  `= (180 (60\ – cos alpha))/sqrt(901\ – 30 cos alpha)\ \ text(km/hr)`