SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Complex Numbers, SPEC1 2024 VCAA 1

Consider the function with rule  \(f(z)=3 z^3+2 i z^2+3 z+2 i\),  where  \(z \in C\).

  1. Verify that  \(3 z+2 i\)  is a factor of \(f(z)\).   (1 mark)

  2. Hence or otherwise, solve the equation  \(f(z)=0\).   
  3. Give your answers in Cartesian form.  (2 marks)

  4. Plot the solutions of  \(f(z)=0\)  on the Argand diagram below.  (1 mark)

Show Answers Only

a.   \(\text{Method 1}\)

\(f(z)=3 z^3+2 i z^2+3 z+2 i = (3z+2i)(z^2+1)\)
 

\(\text{Method 2}\)

\(f\left( -\dfrac{2i}{3} \right)=\dfrac{8}{9}-\dfrac{8}{9}-2i+2i=0\)

\(\text{By factor theorem:}\)

\(z+ \dfrac{2}{3} i\ \ \text{is a factor of}\ f(z) \)

\(\text{Hence,}\ 3\left( z+\dfrac{2i}{3} \right) = 3z+2i\ \ \text{is a factor.}\)
 

b.   \(f(z)= (3z+2i)(z^2+1)\)

\(z=-\dfrac{2i}{3} , z= \pm i\)
 

c.   
         

Show Worked Solution

a.   \(\text{Method 1}\)

\(f(z)=3 z^3+2 i z^2+3 z+2 i = (3z+2i)(z^2+1)\)
 

\(\text{Method 2}\)

\(f\left( -\dfrac{2i}{3} \right)=\dfrac{8}{9}-\dfrac{8}{9}-2i+2i=0\)

\(\text{By factor theorem:}\)

\(z+ \dfrac{2}{3} i\ \ \text{is a factor of}\ f(z) \)

\(\text{Hence,}\ 3\left( z+\dfrac{2i}{3} \right) = 3z+2i\ \ \text{is a factor.}\)
 

b.   \(f(z)= (3z+2i)(z^2+1)\)

\(z=-\dfrac{2i}{3} , z= \pm i\)
 

c.   
         

♦ Mean mark (c) 49%.

Complex Numbers, SPEC2 2020 VCAA 6 MC

For the complex polynomial  `P(z) = z^3 + az^2 + bz + c`  with real coefficients  `a, b` and `c, P(−2) = 0`  and  `P(3i) = 0`.

The values of  `a, b` and `c`  are respectively

  1. `− 2, 9,− 18`
  2. `3, 4, 12`
  3. `2, 9, 18`
  4. `−3, −4, 12`
  5. `2, −9, −18`
Show Answers Only

`C`

Show Worked Solution

`text(S)text(ince coefficients are real,)`

`P(3i) = 0 => P(−3i) = 0\ \ (text(conjugate root theorem))`

`P(z)` `= (z + 2)(z – 3i)(z + 3i)`
  `= z^3 + 2z^2 + 9z + 18`

 
`:. a = 2, b = 9, c = 18`

`=> C`

Complex Numbers, SPEC1 2020 VCAA 3

Find the cube roots of  `1/sqrt 2 - 1/sqrt 2 i`. Express your answers in polar form using principal values of the argument.  (3 marks)

Show Answers Only

`z_1 = text(cis)((7 pi)/12)`

`z_2 = text(cis)(-pi/12)`

`z_3 = text(cis)((-3 pi)/4)`

Show Worked Solution

`z^3 = 1/sqrt 2 – 1/sqrt 2 i = text(cis)(-pi/4) = text(cis)(-pi/4 + 2 pi k), k ∈ Z`
 

`text(By De Moivre):`

`z = text(cis)(-pi/12 + (2 pi k)/3)`

`text(If)\ \ k = 1, \ z_1 = text(cis)(-pi/12 + (2 pi)/3) = text(cis)((7 pi)/12)`

`text(If)\ \ k = 0, \ z_2 = text(cis)(-pi/12)`

`text(If)\ \ k = – 1, \ z_3= text(cis)(-pi/12 – (2pi)/3) = text(cis)((-3 pi)/4)`

Complex Numbers, SPEC2-NHT 2019 VCAA 2

A cubic polynomial has the form  `p(z) = z^3 + bz^2 + cz + d, \ z ∈ C`, where  `b, c, d ∈ R`.

Given that a solution of  `p(z) = 0`  is  `z_1 = 3 - 2i`  and that  `p(–2) = 0`, find the values of  `b, c` and `d`.   (4 marks)

Show Answers Only

`b =-4 \ , \ c = 1 \ , \ d = 26`

Show Worked Solution

`text(Roots:)\  \ z_1 = 3 – 2i \ , \ z_2 = 3 + 2i \ , \ z_3 = -2`
 

`p(z)` `= (z – 3 + 2i )(z – 3 – 2i )(z + 2)`
  `= ((z-3)^2 – (2i)^2)(z+2)`
  `= (z^2 – 6z + 9 + 4)(z + 2)`
  `= (z^2 – 6z + 13)(z + 2)`
  `= z^3 + 2z^2 – 6z^2 – 12z + 13z + 26`
  `= z^3 – 4z^2 + z + 26`

 

`:. \ b =-4 \ , \ c = 1 \ , \ d = 26`

Complex Numbers, SPEC2 2011 VCAA 8 MC

On the argand diagram below, the twelve points  `P_1, P_2, P_3 …, P_12`  are evenly spaced around the circle of radius 3.
 

SPEC2 2011 VCAA 8 MC
 

The points which represent complex numbers such that  `z^3 = -27i`  are

A.   `P_10` only

B.   `P_4` only

C.   `P_2, P_6, P_10`

D.   `P_3, P_7, P_11`

E.   `P_4, P_8, P_12`

Show Answers Only

`E`

Show Worked Solution

`z^3 = 27text(cis)(−pi/2)`

♦ Mean mark 49%.

`:. z_1 = 3text(cis)(−pi/6)\ \ text(is one root.)`

`text(The other two are evenly spaced around the circle)`

`text(which separates them by)\ \ (2pi)/3.`

`=> E`

Complex Numbers, SPEC1 2012 VCAA 3

Consider the equation  `z^3-z^2-2z-12 = 0, \ z in C.`

  1. Given that  `z = 2 text(cis) ((2pi)/3)`  is a root of the equation, find the other two roots in the form  `a + ib`, where  `a, b in R.`   (3 marks)

  2. Plot all of the roots clearly on the Argand diagram below.   (1 mark)

     

     


Show Answers Only
  1. `z_2 = -1-i sqrt 3`
    `z_3 = 3 + 0i`
     

  2.  

Show Worked Solution

a.   `text(Given)\ \  z = 2 text(cis)((2 pi)/3)\ \ text(is a root, and)`

`z^3-z^2-2z-12 = 0\ \ text(has real coefficients,)`

`=> z= 2 text(cis)(-(2 pi)/3)\ \ text{is a root (conjugate).}`

`=> text(Roots:)\ \ -1+sqrt3i,\ \ -1-sqrt3i`
 

`(z-alpha) (z-beta) (z-gamma) = z^3-z^2-2z-12`
 

`text(Using)\ \ alpha beta gamma = 12:`

`(-1 + i sqrt 3) (-1-i sqrt 3) gamma` `=12`  
`((-1)^2-(sqrt3i)^2)gamma` `=12`  
`4gamma` `=12`  
`gamma` `=3`  

 
`:.\ text(Other two roots:)`

♦♦ Mean mark part (b) 33%.

`z_2` `= -1-i sqrt 3`
`z_3` `= 3 + 0i`

 

b.   

Complex Numbers, SPEC2 2016 VCAA 4 MC

One of the roots of   `z^3 + bz^2 + cz = 0`  is  `3 - 2i`, where `b` and `c` are real numbers.

The values of `b` and `c` respectively are

A.  `6, 13`

B.  `3, -2`

C.  `-3, 2`

D.  `2, 3`

E.  `-6, 13` 

Show Answers Only

`E`

Show Worked Solution

`z(z^2 + bz + c) = 0,\ b, c in RR`

`text(Given)\ \ z= 3 – 2i \ \ text(is a root,)`

`=> z = 3 + 2i\ \ text{is a root (conjugate).}`
 

`z(z^2 + bz + c)` `= 0`
`z((z – 3) + 2i)((z – 3) – 2i)` `= 0`
`z((z – 3)^2 – 4i^2)` `= 0`
`z(z^2 – 6z + 9 + 4)` `= 0`
`z^3 – 6z^2 + 13z` `= 0`

 
`b = -6,\ \ c = 13` 

`=>  E`

Complex Numbers, SPEC2-NHT 2017 VCAA 2

One root of a quadratic equation with real coefficients is  `sqrt 3 + i`.

    1. Write down the other root of the quadratic equation.   (1 mark)

    2. Hence determine the quadratic equation, writing it in the form  `z^2 + bz + c = 0`.   (2 marks)

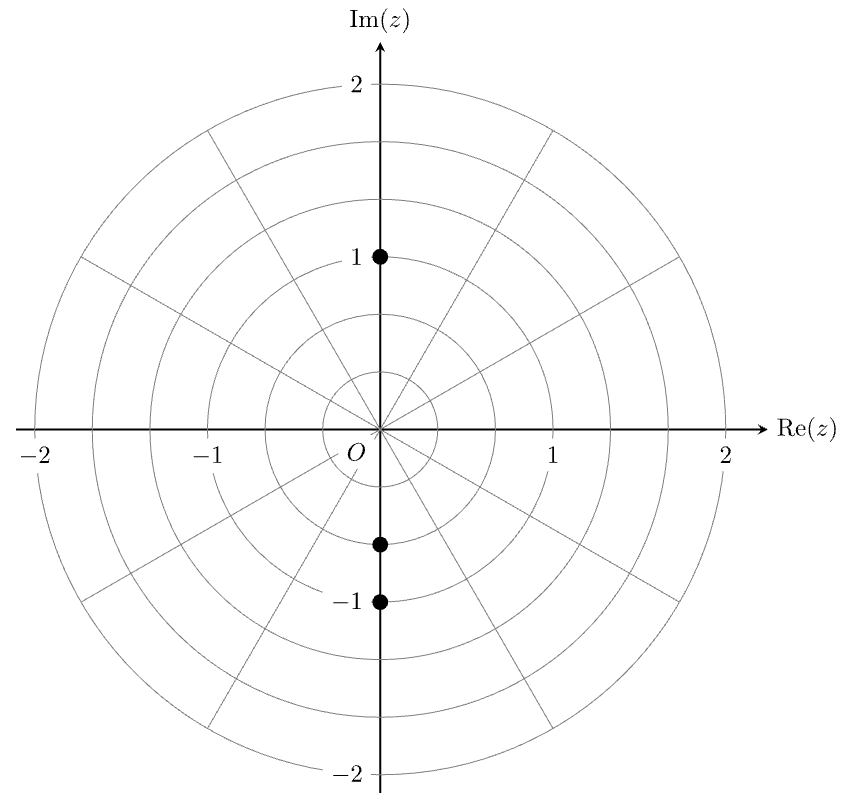
  1. Plot and label the roots of   `z^3-2 sqrt 3 z^2 + 4z = 0`  on the Argand diagram below.   (3 marks)

  

 

  1. Find the equation of the line that is the perpendicular bisector of the line segment joining the origin and the point  `sqrt 3 + i`. Express your answer in the form  `y = mx + c`.   (2 marks)

  1. The three roots plotted in part b. lie on a circle.

     

    Find the equation of this circle, expressing it in the form  `|z-alpha| = beta`,  where  `alpha, beta in R`.   (3 marks)

Show Answers Only
    1. `z_2 = sqrt 3-i`
    2. `z^2-2 sqrt 3 z + 4 = 0`
  2. `text(See Worked Solutions)`
  3. `y = -sqrt 3 x + 2`
  4. `|z-2/sqrt 3 | = 2/sqrt 3`
Show Worked Solution

a.i.   `z_1 = sqrt 3 + i`

 `z_2 = bar z_1 = sqrt 3-i\ \ \ text{(conjugate root)}`

 

a.ii.    `(z-(sqrt 3 + i))(z-(sqrt 3-i))` `= 0`
  `((z-sqrt 3)-i)((z-sqrt 3) + i)` `= 0`
  `(z-sqrt 3)^2-i^2` `= 0`
  `z^2-2 sqrt 3 z + 3 + 1` `= 0`
  `z^2-2 sqrt 3 z + 4` `= 0`

 

b.    `z(z^2-2 sqrt 3 z + 4)` `= 0`
  `z(z-(sqrt 3 + i))(z-(sqrt 3-i))` `= 0`

 
`text(Convert to polar form:)`

  `sqrt 3 + i` `= sqrt((sqrt 3)^2 + 1^2) * text(cis) (tan^(-1)(1/sqrt 3))`
    `= 2 text(cis) (pi/6)`
  `=> sqrt 3-i` `= 2 text(cis) (-pi/6)`

 

   

 

c.   `text(Equidistant from)\ (0, 0) and (sqrt 3, 1)`

`text(Midpoint)\ (x_1, y_1)` `= (sqrt 3/2, 1/2)`

 
`m = (1-0)/(sqrt 3-0) = 1/sqrt 3`

`m_(_|_) = (-1)/m = -sqrt 3`
 

`:.\ text(Equation of ⊥ bisector:)`

`y-1/2` `=-sqrt3(x-sqrt3/2)`  
`y` `=-sqrt3 x +3/2+1/2`  
`:.y` `=-sqrt3 x +2`  

 

d.   `text(Let)\ O = (0, 0),\ P = (sqrt 3, 1),\ Q = (sqrt 3, -1)`

`text(⊥ bisector of two points on arc of a circle passes)`

`text(through the centre of the circle.)`
 

`OP = OQ = PQ = 2`

`=> Delta OPQ\ text(is equilateral)`
 

`text(⊥ bisector of)\ PQ\ text(is)\ y=0.`

`text(Centre of circle occurs when:)`

`0 = -sqrt 3 x + 2\ \ text{(using part c)`

`x=2/sqrt3`

`=>\ text(Radius)\ = 2/sqrt3`
 

`:. |z-2/sqrt 3| = 2/sqrt 3`

Complex Numbers, SPEC1-NHT 2017 VCAA 4

Find the values of `a` and `b` given that  `z - 1 - i`  is a factor of  `z^3 + (a + b)z^2 + (b^2 - a)z - 4 = 0`, where `a` and `b` are real constants.  (4 marks)

Show Answers Only

`(a, b) = (-5, 1) or (-2, -2)`

Show Worked Solution

`text(All coefficients are real):`

`=> z – 1 + i \ \  text{is a factor (conjugate pair)}`

`(z – 1 – i) (z – 1 + i)` `= ((z – 1) – i)((z – 1) + i)`
  `= (z – 1)^2 – i^2`
  `= z^2 – 2z + 1 + 1`
  `= z^2 – 2z + 2`

 
`(z – alpha)(z^2 – 2z + 2)`

`=z^3 -2z^2 + 2z -alpha z^2 +2 alpha z – 2 alpha, \ \ \ alpha in RR`

`=z^3 + (-alpha – 2)z^2 + (2 alpha + 2)z – 2 alpha`

`= z^3 + (a + b)z^2 + (b^2 – a) z – 4`
 

`text(Equating coefficients:)`

`2 alpha = -4 \ \ =>\ \ alpha = 2`

`a + b = -4 \ \ …\ (1)`

`b^2 – a = 6 \ \ …\ (2)`

 
`text{Substitute}\ \ a=-b-4\ \ text{from (1) into (2):}`

`b^2 – (-4 – b)` `= 6`
`b^2 + b + 4` `= 6`
`b^2 + b – 2` `=0`
`(b + 2)(b – 1)` `=0`

 
`b = 1\ \ => \ \ a=-5, \ text(or)`

`b=-2\ \ => \ \ a = -4 + 2=-2`

`:. (a, b) = (-5, 1) or (-2, -2)`

Complex Numbers, SPEC1 2015 VCAA 4

  1. Find all solutions of  `z^3 = 8i,  \ z in C` in cartesian form.   (3 marks)

  2. Find all solutions of  `(z − 2i)^3 = 8i, \ z in C`  in cartesian form.   (1 mark)

Show Answers Only
  1. `-2i, +- sqrt 3 + i`
  2. `z = 0 or z = +- sqrt 3 + 3i`
Show Worked Solution

a.   `z^3 = 8text(cis)(pi/2)`

`z_1` `= 8^(1/3)text(cis)(pi/6)`
  `= 2text(cis)(pi/6)`
  `= sqrt3 + i`
   
`z_2` `= 2text(cis)(pi/6 + (2pi)/3)`
  `= 2text(cis)((5pi)/6)`
  `= −sqrt3 + i`
   
`z_3` `= 2text(cis)(pi/6-(2pi)/3)`
  `= 2text(cis)(−pi/2)`
  `= −2i`

 
`:. z = sqrt3 + i, \ −sqrt3 + i, \ −2i`
 

♦ Mean mark part (b) 44%.

b.    `z_1-2i` `= sqrt3 + i`
  `z_1` `= sqrt3 + 3i`
     
`z_2-2i` `= −sqrt3 + i`
`z_2` `= −sqrt3 + 3i`
   
`z_3-2i` `= −2i`
`z_3` `= 0`

 
`:. z = sqrt3 + 3i, \ −sqrt3 + 3i, \ 0`

Complex Numbers, SPEC2 2014 VCAA 7 MC

The sum of the roots of  `z^3 - 5z^2 + 11z - 7 = 0`,  where  `z ∈ C`,  is

  1. `1 + 2sqrt3i`
  2. `5i`
  3. `4 - 2sqrt3i`
  4. `2sqrt3i`
  5. `5`
Show Answers Only

`E`

Show Worked Solution

`text(Coefficients are real)`

`=>\ text(Conjugate root theorem applies.)`

`z_1=alpha + beta i,\ \ z_2=alpha – beta i, \ \ z_3=gamma`

`z_1+z_2+z_3` `= alpha + beta i + alpha – beta i + gamma`
  `= 2 alpha + gamma\ \ \ (∈R)`

 

`=> E`

Complex Numbers, SPEC1 VCAA 2017 3

Let  `z^3 + az^2 + 6z + a = 0, \ z ∈ C`, where `a` is a real constant.

Given that  `z = 1 - i`  is a solution to the equation, find all other solutions.  (3 marks)

Show Answers Only
`z_2` `= 1 + i`
`z_3` `= 2`
Show Worked Solution

`z_1 = 1 – i`

`=>\ z_2 = 1 + i\ \ text{(conjugate pair)}`

`=>\ z_3 ∈ R`
 

`z^3 + az^a + 6z + a`

  `= (z – z_1)(z – z_2)(z – z_3)`
  `= (z – (1 – i))(z – (1 + i))(z – z_3)`
  `= ((z – 1) + i)((z – 1) – i)(z – z_3)`
  `= ((z – 1)^2 – i^2)(z – z_3)`
  `= (z^2 – 2z + 1 + 1)(z – z_3)`
  `= (z^2 – 2z + 2)(z – z_3)`
  `= z^3 – (z + z_3)z^2 + (2z_3 + 2)z – 2z_3`

 
`text(Equating the co-efficients of)\ \ z:`

`6` `= 2z_3 + 2`
`4` `= 2z_3`
`z_3` `= 2`

 
`:.\ text(Other solutions are:)`

`z_2` `= 1 + i`
`z_3` `= 2`

Complex Numbers, SPEC2-NHT 2018 VCAA 6 MC

Given that  `(z - 3i)`  is a factor of  `P(z) = z^3 + 2z^2 + 9z + 18`, which one of the following statements is false?

  1. `P(3i) = 0`
  2. `P(-3i) = 0`
  3. `P(z)`  has three linear factors over `C`
  4. `P(z)`  has no real roots
  5. `P(z)`  has two complex conjugate roots
Show Answers Only

`D`

Show Worked Solution

`z – 3i\ \ text(is a factor) \ => \ z + 3i\ text(is a factor)`

`text(deg) (P) = 3`

`text(Complex roots occur in conjugate pairs.)`

`text(S)text(ince 3 roots → 3rd root must be real.)`

`=>   D`