The direction field shown above best represents the differential equation
Calculus, SPEC2 2023 VCAA 7 MC
The direction field for a differential equation is shown above. On a certain solution curve of this differential equation,
The value of
Calculus, EXT1 C3 2022 HSC 12a
A direction field is to be drawn for the differential equation
On the diagram, clearly draw the correct slopes of the direction field at the points
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
Calculus, SPEC2 2021 VCAA 10 MC
The differential equation that has the diagram above as its direction field is
Calculus, EXT1 C3 2021 HSC 12a
The direction field for a differential equation is shown below.
The graph of a particular solution to the differential equation passes through the point
On the graph, sketch the graph of this particular solution. (1 mark)
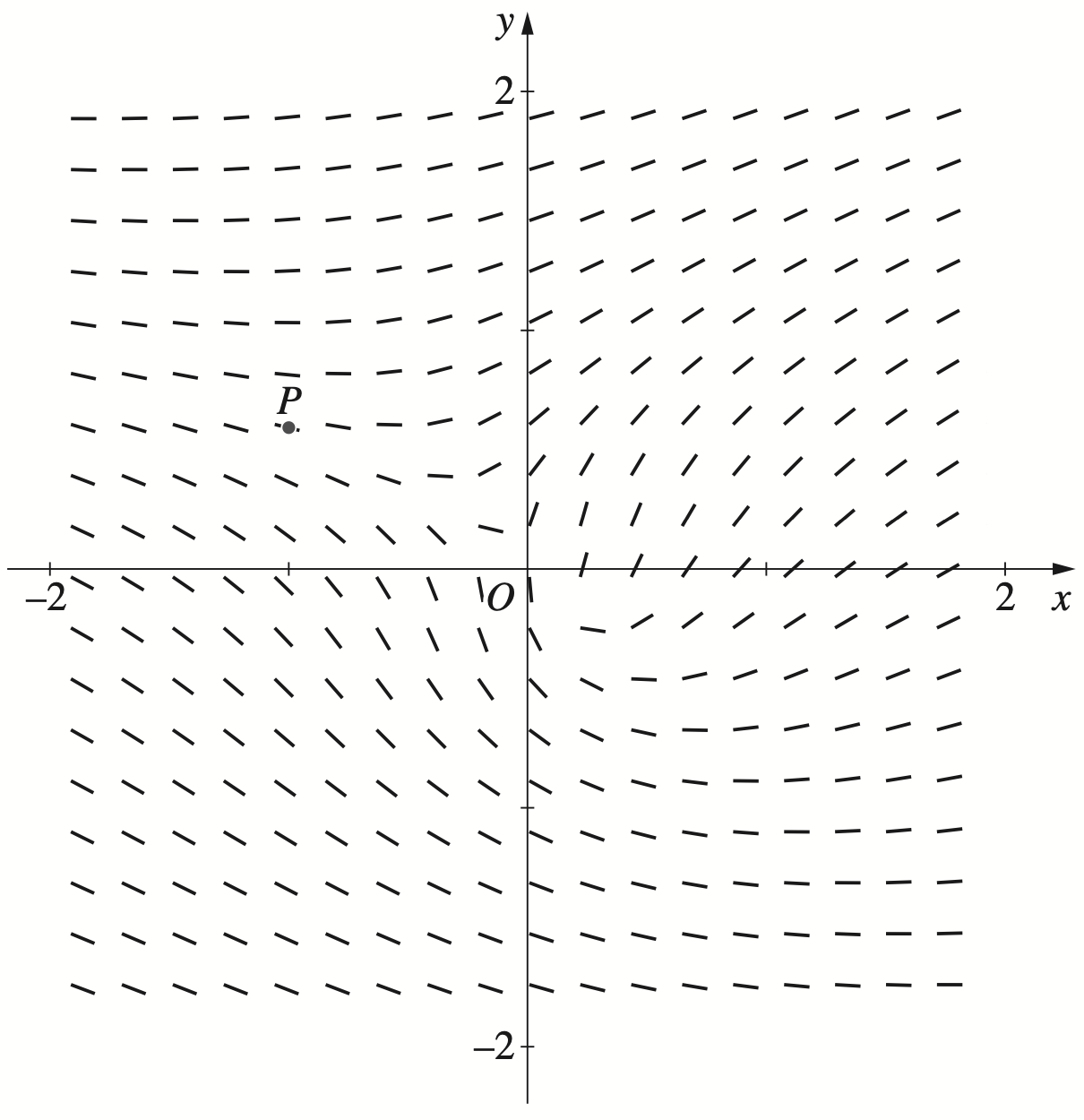
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
♦♦♦ Mean mark 18%!
MARKER COMMENT: A solution curve does not cross any tangent line.
MARKER COMMENT: A solution curve does not cross any tangent line.
Calculus, SPEC2 2020 VCAA 9 MC
Which one of the following slope fields best represents this curve?
| A. |  |
B. |  |
| C. |  |
D. |  |
| E. |  |
Calculus, SPEC2 2019 VCAA 9 MC
The differential equation that has the diagram above as its direction field is
Calculus, SPEC2 2012 VCAA 10 MC
The diagram that best represents the direction field of the differential equation
| A. |  |
B. |  |
| C. |  |
D. |  |
Calculus, SPEC2 2011 VCAA 17 MC
The differential equation which best represents the above direction field is
A.
B.
C.
D.
E.
Calculus, SPEC2 2013 VCAA 12 MC
The differential equation that best represents the above direction field is
A.
B.
C.
D.
E.
Calculus, SPEC2 2014 VCAA 14 MC
The differential equation that is best represented by the above direction field is
A.
B.
C.
D.
E.
Calculus, SPEC2 2015 VCAA 13 MC
The direction field for a certain differential equation is shown above.
The solution curve to the differential equation that passes through the point
A.
B.
C.
D.
E.
Show Worked Solution
♦ Mean mark 47%.
Calculus, SPEC2 2016 VCAA 10 MC
The direction field for the differential equation
A solution to this differential equation that includes
A.
B.
C.
D.
E.
Show Worked Solution
Calculus, SPEC2-NHT 2017 VCAA 8 MC
The differential equation that best represents the direction field above is
A.
B.
C.
D.
E.
Calculus, SPEC1 2017 VCAA 8
A slope field representing the differential equation
- Sketch the solution curve of the differential equation corresponding to the condition
on the slope field above and, hence, estimate the positive value of when . Give your answer correct to one decimal place. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
- Solve the differential equation
with the condition . Express your answer in the form , where , , and are integers. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
| a. |  |
♦♦ Mean mark part (a) 32%.
MARKER’S COMMENT: Solution curve should follow slope ticks and not cross them.
MARKER’S COMMENT: Solution curve should follow slope ticks and not cross them.
| b. | ||
Calculus, SPEC2 2018 VCAA 10 MC
The differential equation that best represents the direction field above is
A.
B.
C.
D.
E.