The diagram shows the direction field of a differential equation. A particular solution to the differential equation passes through
Where does the solution that passes through
Calculus, EXT1 C3 2022 HSC 12a
A direction field is to be drawn for the differential equation
On the diagram, clearly draw the correct slopes of the direction field at the points
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
Calculus, EXT1 C3 2021 SPEC2 10 MC
The differential equation that has the diagram above as its direction field is
Calculus, EXT1 C3 2021 HSC 12a
The direction field for a differential equation is shown below.
The graph of a particular solution to the differential equation passes through the point
On the graph, sketch the graph of this particular solution. (1 mark)
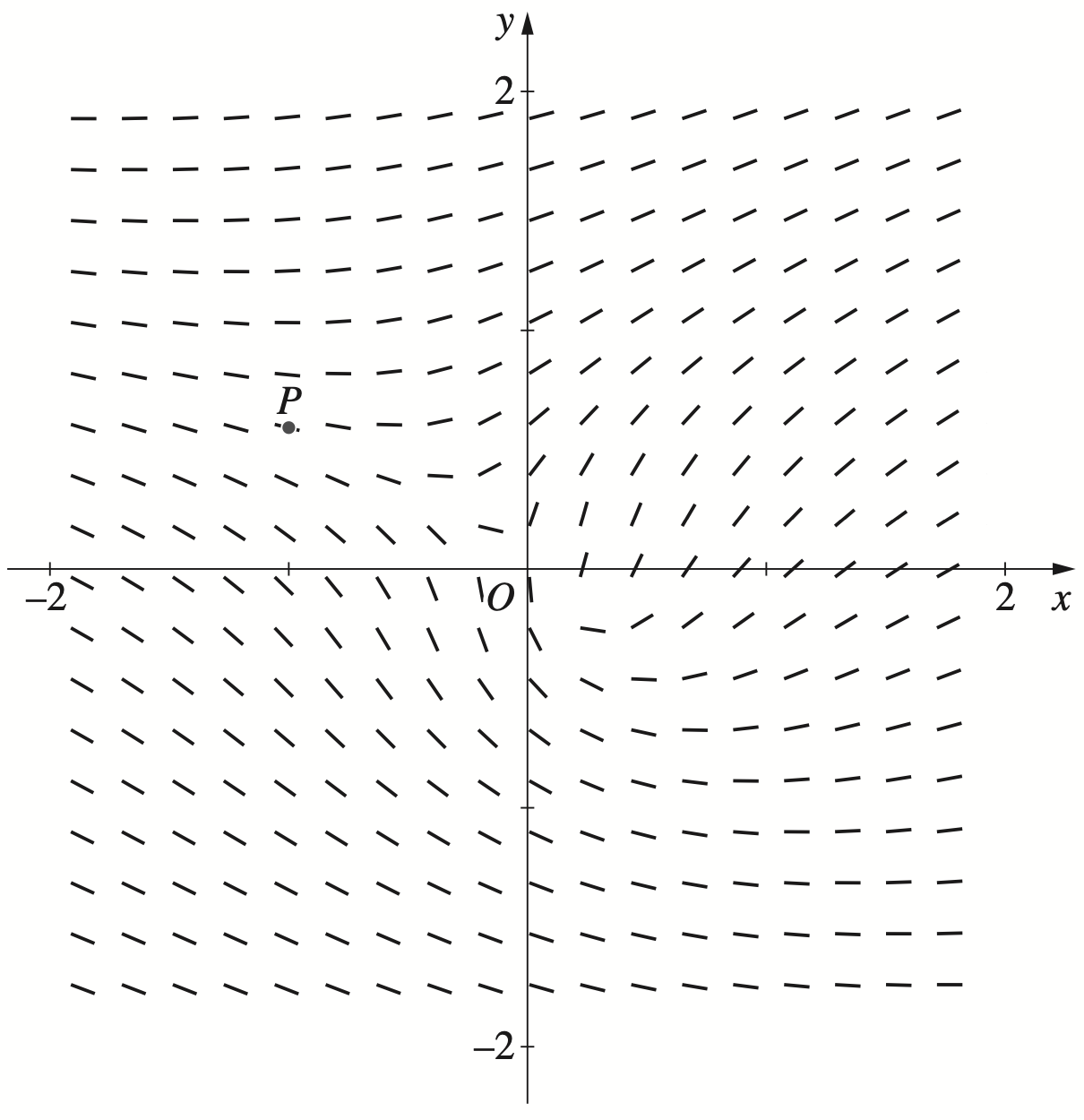
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
♦♦♦ Mean mark 18%!
MARKER COMMENT: A solution curve does not cross any tangent line.
MARKER COMMENT: A solution curve does not cross any tangent line.
Calculus, EXT1 C3 2020 SPEC2 9 MC
Which one of the following slope fields best represents this curve?
| A. |  |
B. |  |
| C. |  |
D. |  |
Calculus, EXT1 C3 2020 HSC 7 MC
Which of the following best represents the direction field for the differential equation
| A. |  |
B. |  |
| C. |  |
D. |  |
Calculus, EXT1 C3 2019 SPEC2 9 MC
The differential equation that has the diagram above as its direction field is
Calculus, EXT1 C3 2017 SPEC1 8
A slope field representing the differential equation
- Sketch the solution curve of the differential equation corresponding to the condition
on the slope field above and, hence, estimate the positive value of when . Give your answer correct to one decimal place. (2 marks) - Solve the differential equation
with the condition . Express your answer in the form , where , , and are integers. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
| a. |  |
♦♦ Mean mark part (a) 32%.
MARKER’S COMMENT: Solution curve should follow slope ticks and not cross them.
MARKER’S COMMENT: Solution curve should follow slope ticks and not cross them.
| b. | ||
Calculus, EXT1 C3 2015 SPEC2 13 MC
The direction field for a certain differential equation is shown above.
The solution curve to the differential equation that passes through the point
A.
B.
C.
D.
Show Worked Solution
♦ Mean mark 47%.
Calculus, EXT1 C3 2017 SPEC2 8 MC
The differential equation that best represents the direction field above is
A.
B.
C.
D.
Calculus, EXT1 C3 2018 SPEC2 10 MC
The differential equation that best represents the direction field above is
A.
B.
C.
D.
Calculus, EXT1 C3 2016 SPEC2 10 MC
The direction field for the differential equation
A solution to this differential equation that includes
A.
B.
C.
D.
Show Worked Solution
Calculus, EXT1 C3 2014 SPEC2 14 MC
The differential equation that is best represented by the above direction field is
A.
B.
C.
D.
Calculus, EXT1 C3 2013 SPEC2 12 MC
The differential equation that best represents the above direction field is
A.
B.
C.
D.
Calculus, EXT1 C3 2012 SPEC2 10 MC
The diagram that best represents the direction field of the differential equation
| A. |  |
B. |  |
| C. |  |
D. |  |
Calculus, EXT1 C3 2011 SPEC2 17 MC
The differential equation which best represents the above direction field is
A.
B.
C.
D.
E.
Calculus, EXT1 C3 2017 SPEC2 9 MC
The gradient of the tangent to a curve at any point
The coordinates of points on the curve satisfy the differential equation
A.
B.
C.
D.