Part of the graph of
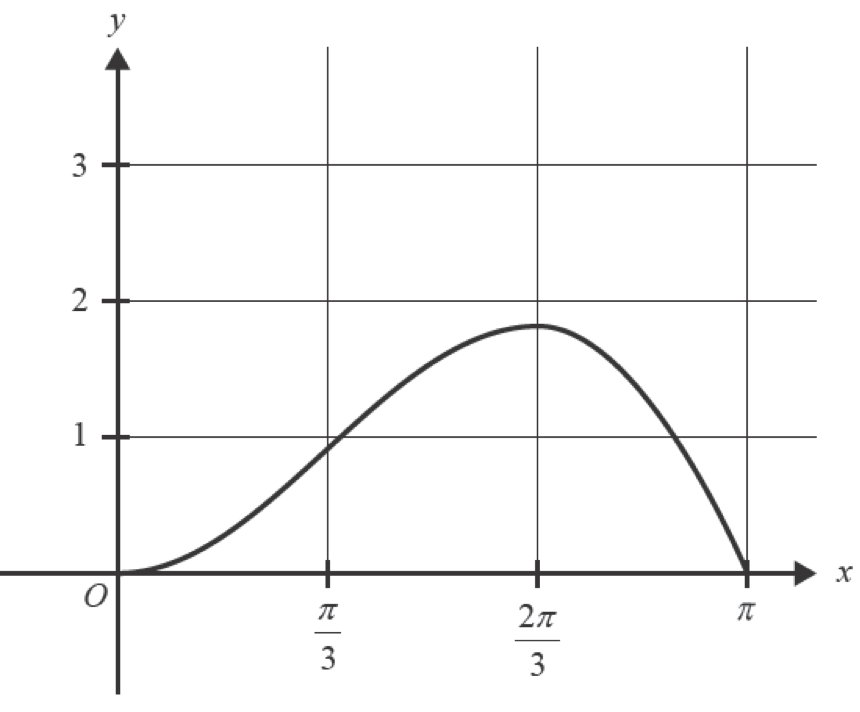
- Use the trapezium rule with a step size of
to determine an approximation of the total area between the graph of and the -axis over the interval . (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
- i. Find
. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- ii. Determine the range of
over the interval . (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- iii. Hence, verify that
has a stationary point for . (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- On the set of axes below, sketch the graph of
on the domain , labelling the endpoints with their coordinates. - You may use the fact that the graph of
has a local minimum at approximately and a local maximum at approximately . (3 marks)
--- 0 WORK AREA LINES (style=lined) ---










