SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

ENGINEERING, CS 2023 HSC 13 MC

Which mechanical property describes an object that is under load and follows Hooke's Law?

  1. Ductility
  2. Elasticity
  3. Malleability
  4. Plasticity
Show Answers Only

\(  B \)

Show Worked Solution
  • Hooke’s law states that for relatively small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load.
  • Hooke’s law is a fundamental principle in understanding the behaviour of elastic materials.

\(\Rightarrow  B \)

ENGINEERING, CS 2018 HSC 23b

The steel used in the chassis members was tested.

The load–extension graph represents the data collected during the testing of a specimen of the steel.
 

Before testing, the specimen was 1020 mm long with a cross-sectional area of 100 mm².

  1. Calculate Young's modulus for this steel.   (4 marks)
  1. Describe the physical changes that occur in the specimen tested in part (i) when a 20 kN load is applied and then removed, compared to when a 30 kN load is applied and then removed.   (2 marks)
Show Answers Only

i.   Young’s modulus

`F = 20 xx 10^3\ text{N}, l = 1020\ text{mm},  e = 1\ text{mm},  text{A} = 100\ text{mm}^2`

`E` `=(Fl)/(eA)`  
  `=(20 xx 10^3 xx1020)/(1 xx 100)`  
  `=204 xx 10^3`  
  `=204\ text{GPa}`  

ii.   

  • Elastic deformation is produced by the 20 kN load.
  • After initial stretching the specimen returns to its original length.
  • Plastic deformation is produced by the 30 kN load.
  • The specimen stays deformed subsequent to release.
Show Worked Solution

i.   Young’s modulus

`F = 20 xx 10^3\ text{N}, l = 1020\ text{mm},  e = 1\ text{mm},  text{A} = 100\ text{mm}^2`

`E` `=(Fl)/(eA)`  
  `=(20 xx 10^3 xx1020)/(1 xx 100)`  
  `=204 xx 10^3`  
  `=204\ text{GPa}`  

♦ Mean mark (i) 51%.

ii.     Elastic deformation is produced by the 20 kN load.

  • After initial stretching the specimen returns to its original length.
  • Plastic deformation is produced by the 30 kN load.
  • The specimen stays deformed subsequent to release.

ENGINEERING, CS 2016 HSC 21aiii

The reinforced concrete modules shown are designed for public seating. A typical use would be as a bus shelter.
 

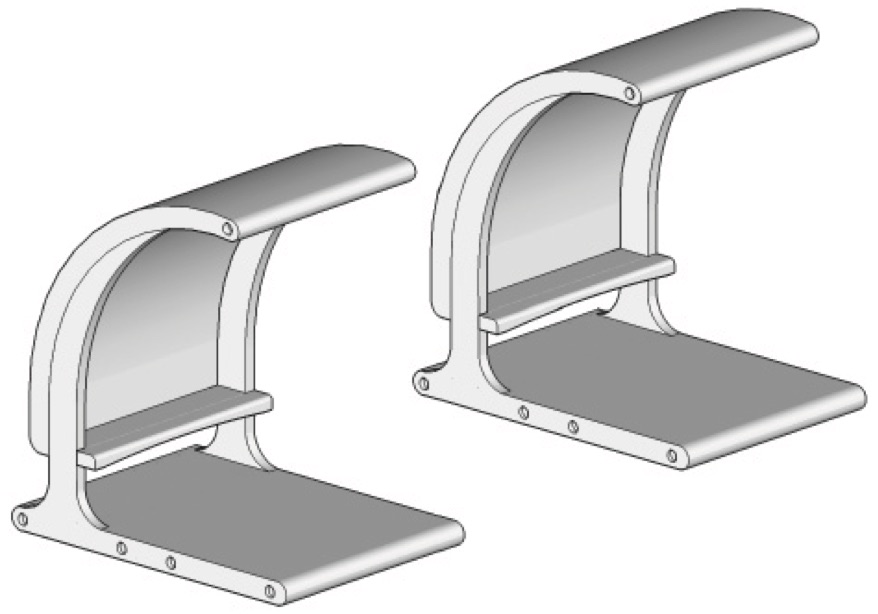
A 12 mm diameter steel reinforcing bar was used in this seating module. During a proof test, a load of 26 kN extended a 0.9 m length of this reinforcing bar by 1 mm.

Calculate the value of Young's Modulus (E) for this bar.   (3 marks)

Show Answers Only

`206.9\ text{GPa}`

Show Worked Solution

`sigma=F/A=(26\ 000)/(pixx6^2)229.9\ text{MPa}`

`epsilon=e/L=1/900=1.1111 xx 10^-3`

`E` `=sigma/epsilon`  
  `=229.9/(1.1111 xx 10^-3)\  text{MPa}`  
  `=206.9 xx 10^3\ text{MPa}`  
  `=206.9\ text{GPa}`  

 

Mean mark 56%.

ENGINEERING, CS 2018 HSC 2 MC

The diagram shows a scaffold with diagonal braces.
 

When loaded, the diagonal braces are typically subjected to which pair of forces?

  1. Torsion and shear
  2. Torsion and tension
  3. Compression and shear
  4. Compression and tension
Show Answers Only

`D`

Show Worked Solution
  • Bracing members can only carry tension, or both tension and compression.

`=>D`


♦ Mean mark 53%.

ENGINEERING, CS 2017 HSC 27a

Why is the routine testing of engineering components important during service?   (2 marks)

Show Answers Only
  • Aircraft jet engines, diesel trucks, structural beams and a myriad of other engineering components are subject to heavy loads, polluted and corrosive environments, and high operating cycles.
  • It is important to maintain regular routine testing to help guarantee that dangerous conditions or possible faults do not occur.
  • This type of testing has a key role in safeguarding the public as well as increasing the longevity and economic benefit of engineering components.
Show Worked Solution
  • Aircraft jet engines, diesel trucks, structural beams and a myriad of other engineering components are subject to heavy loads, polluted and corrosive environments, and high operating cycles.
  • It is important to maintain regular routine testing to help guarantee that dangerous conditions or possible faults do not occur.
  • This type of testing has a key role in safeguarding the public as well as increasing the longevity and economic benefit of engineering components.
Mean mark 59%.

ENGINEERING, CS 2019 HSC 21a

A bus shelter is shown.

The design of this bus shelter includes the use of toughened glass panels.

Outline advantages of using toughened glass for this bus shelter.   (3 marks)

Show Answers Only
  • Flexural strength is high.
  • The risk of serious injury is reduced as toughened glass breaks into smaller pieces when broken by applied load.
  • Withstands chipping during transportation and insulation due to strong edge strength.
Show Worked Solution
  • Flexural strength is high.
  • The risk of serious injury is reduced as toughened glass breaks into smaller pieces when broken by applied load.
  • Withstands chipping during transportation and insulation due to strong edge strength.

Mean mark 55%.

ENGINEERING, CS 2019 HSC 20 MC

An annealed copper tensile test specimen has an original cross-sectional area (CSA) of 100 mm².

During testing, an engineering stress of 150 MPa is induced within the specimen before necking occurs. At this strain the CSA reduces uniformly by 10% to 90 mm².

This is illustrated in the diagrams below.
 

What is the value of the true stress induced at this strain?

  1. 135.0 MPa
  2. 136.4 MPa
  3. 150.0 MPa
  4. 166.7 MPa
Show Answers Only

`D`

Show Worked Solution
`sigma` `= F/A`  
`150\ 000\ 000` `= F/0.0001`  
`F` `= 15000\ text{N}`  

  
`:.\  sigma\ _(text{True})= (15\ 000)/90= 166.7\ text{MPa}`

`=>D`


♦ Mean mark 49%.

ENGINEERING, CS 2022 HSC 23b

The diagram represents a 120 kg beam that is being guided into place by a crane.
 

Use a scale drawing to graphically determine the tension in the two cables attached to the beam.   (3 marks)

Show Answers Only

Scale: 1 mm = 20 N


 

Tension in C1 = 1.3 kN

Tension in C2 = 1.06 kN

Show Worked Solution

Scale: 1 mm = 20 N


 

Tension in C1 = 1.3 kN

Tension in C2 = 1.06 kN

(Answers that are relatively similar in either direction will be correct as question asks for graphical solution, creating a margin of error)


♦ Mean mark 46%.

ENGINEERING, CS 2020 HSC 11 MC

The diagram shows a 10 kg lamp hanging from a cable over a cycle path.
 

What is the tension in cable `A` ?

  1. 44 N
  2. 88 N
  3. 100 N
  4. 110 N
Show Answers Only

`B`

Show Worked Solution

Solve graphically:

  • Draw a 10cm vertical line (scale 1 cm = 10 N)
  • Draw other sides of triangle using a protractor for accuracy
  • Measure side A and convert to Newtons using the scale

`=>B`


Mean mark 56%.

ENGINEERING, CS 2021 HSC 19 MC

The diagram shows a simply supported beam in equilibrium. It is loaded with a single force (`text{F}`) as shown.
 

Which of the following angles is closest to the angle of the reaction force to the horizontal at the fixed bearing?

  1. 7°
  2. 14°
  3. 31°
  4. 90°
Show Answers Only

`B`

Show Worked Solution
  • The fixed joint takes half of the vertical force and all of the horizontal force, therefore the angle will be half that of the original force `text{F}`.

`=>B`

♦♦♦ Mean mark 18%.

ENGINEERING, CS 2021 HSC 21b

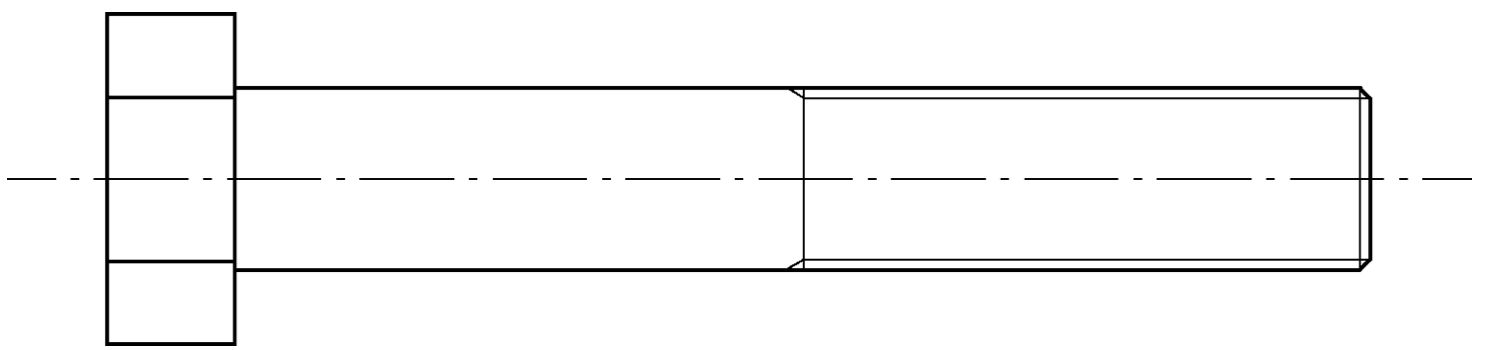
A 100 mm long M16 × 2 bolt is used in the concrete decking of a bridge. The bolt has a thread length of 50 mm.

  1. Draw an orthogonal view, to AS 1100, to show the length of the bolt.
  2. Use the centreline provided and do NOT dimension the drawing. Use a scale of 1:1.   (3 marks)
  1. The yield stress of the bolt is 476 MPa and the diameter is 16 mm.
  2. Calculate the maximum load that the bolt can resist, assuming a Factor of Safety of 2.   (3 marks)
Show Answers Only

i. 

    

ii.   `47.9\ text{kN}`

Show Worked Solution

i. 

    

ii.   Find max load of bolt:

`text{Yield stress} = 476\ text{MPa, Bolt diameter = 16 mm}`

`text{Allowable Stress}= 476 -: 2=238\ text{MPa}`

`text{Area (bolt)}\=pir^2=pi xx 8^2=201.1\ text{mm}^2`

`text{Max Load }` `=\ text{allowable stress × area}`  
  `=238 xx 10^6 xx 201.1 xx 10^(-6)`  
  `=47\ 861.8\ text{N}`  
  `=47.9\ text{kN}`