Which is the correct angle of repose for rock fill, used on a highway construction, that has a coefficient of friction of 0.84?
- 20°
- 30°
- 40°
- 50°
ENGINEERING, PPT 2023 HSC 25d
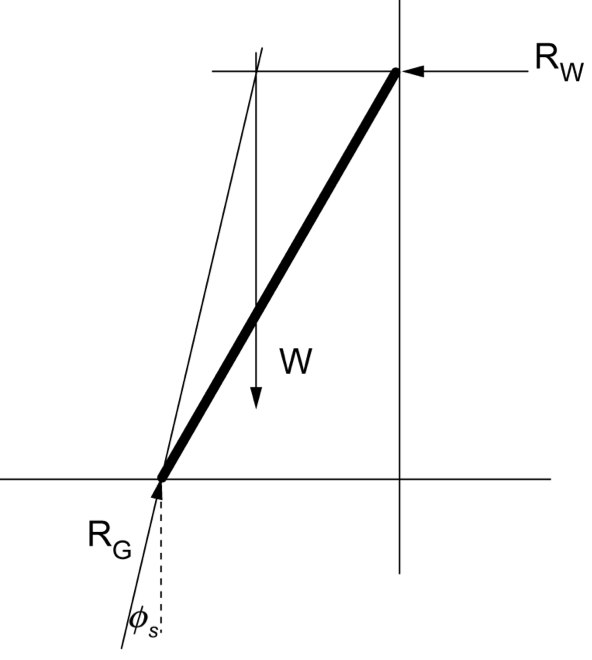
A uniform 8-metre ladder with a mass of 12 kg has been placed against a smooth wall. Determine the minimum coefficient of static friction between the ground and the ladder. Assume there is no friction between the ladder and the wall. (4 marks) --- 5 WORK AREA LINES (style=lined) ---
Graphical solution: \(\phi = 16^{\circ}\) \(\mu = \tan \phi = \tan 16^{\circ} = 0.287\ \text{(3 d.p.)}\) Analytical solution: \(\cos 60^{\circ} = \dfrac{\text{d}_1}{4}\ \Rightarrow \ \text{d}_1 = 2\ \text{m} \) \(\sin 60^{\circ} = \dfrac{\text{d}_2}{8}\ \Rightarrow \ \text{d}_2 = 6.928\ \text{m} \) \(\text{F}_{\text{g}}=mg=120\ \text{N}\)
Show Worked Solution
♦♦ Mean mark 31%.
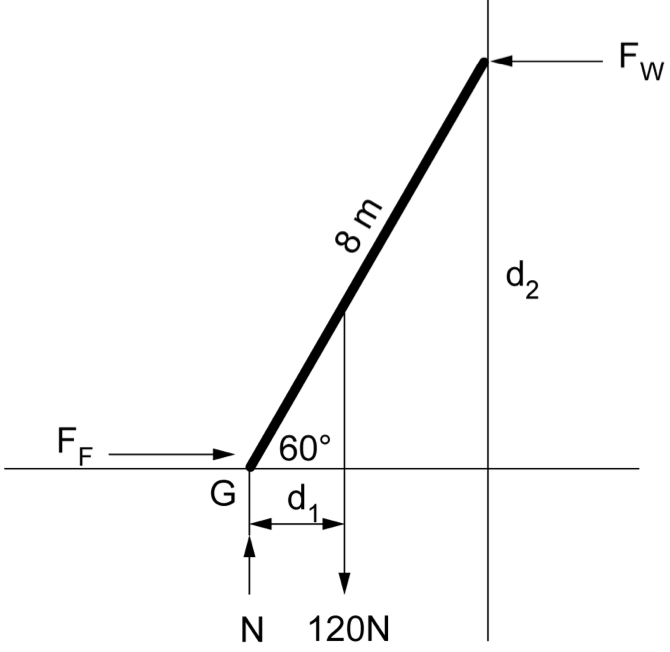
\( \Sigma \text{M}_{\text{G}} \)
\(=0\)
\(0\)
\(=(120 \times 2)-(\text{F}_{\text{W}} \times 6.928) \)
\(\text{F}_{\text{W}}\)
\(=\dfrac{240}{6.928}= 34.64\ \text{N}\)
\(\therefore \text{F}_{\text{F}} = 34.64 \text{ N}\)
\(\therefore \text{N} = 120 \text{N}\uparrow \)
\(\text{F}_{\text{F}}\)
\(= \mu \text{N}\)
\(\mu\)
\(= \dfrac{34.64}{120}=0.289\ \text{(3 d.p.)} \)
ENGINEERING, PPT 2018 HSC 26b
The body of the fidget spinner is made from polypropylene. The bearing is made from steel.
When the force P applied by the press punch is 16 N, the bearing slides into position.
Calculate the normal force (N) acting on the bearing walls if the coefficient of friction between polypropylene and steel is 0.20. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
ENGINEERING, PPT 2018 HSC 20 MC
A box with weight `W` and subject to a friction force `F` is being pulled up an inclined plane by a force `P`.
The force `R` is the resultant of which two forces?
- `P` and `W`
- `P` and `N`
- `F` and `W`
- `F` and `N`
ENGINEERING, PPT 2017 HSC 24b
A child and sled with a combined mass of 23 kg are being pulled along a horizontal snow-covered surface using a rope.
The coefficient of static friction between the sled and the snow is 0.14.
- Draw a free-body diagram that indicates the forces acting on the sled. Label the diagram. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- Calculate the tension in the rope immediately before the point at which the sled and child begin to move. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Show Answers Only
i.
ii. `text{32 N}`
Show Worked Solution
i.
Mean mark (i) 57%.
ii. `text{Weight}\ = mg = 23 xx 10 = 230\ text{N}`
`text{Solving for}\ T:`
`tan^(-1)(0.14) = 8°`
`text{Using the sine rule:}`
| `T/(sin8°)` | `=230/(sin92°)` | |
| `T` | `=(230 xx sin8°)/(sin92°)=32.0\ text{N}` |
`:.\ text{Tension in the rope = 32 N}`
♦ Mean mark (ii) 40%.
ENGINEERING, PPT 2019 HSC 7 MC
A box sits on a horizontal surface. The box begins to slip when this surface is tilted to 28 degrees.
What is the coefficient of friction between the box and the surface?
- 0.280
- 0.469
- 0.532
- 0.883
ENGINEERING, PPT 2021 HSC 26b
The diagram shows a box which is at rest on an inclined ramp. The length of the ramp is 3 m and one end is raised `h` metres off the ground.
The coefficient of friction between the ramp and the box is 0.5.
To what height `(h)` must the ramp be raised for the box to just begin to slide? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
ENGINEERING, PPT 2021 HSC 22d
A skateboard rider is at rest at the top of a slope, indicated by point `A` in the diagram.
The combined mass of the rider and skateboard is 80 kg.
Calculate the speed of the rider, in metres per second, at point `B` if the average work done by friction against the skateboard is 55 N. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---