smc-621-30-Float time/LST

Networks, GEN2 2023 VCAA 14

One of the landmarks in state $A$ requires a renovation project.

This project involves 12 activities, $A$ to $L$. The directed network below shows these activities and their completion times, in days.

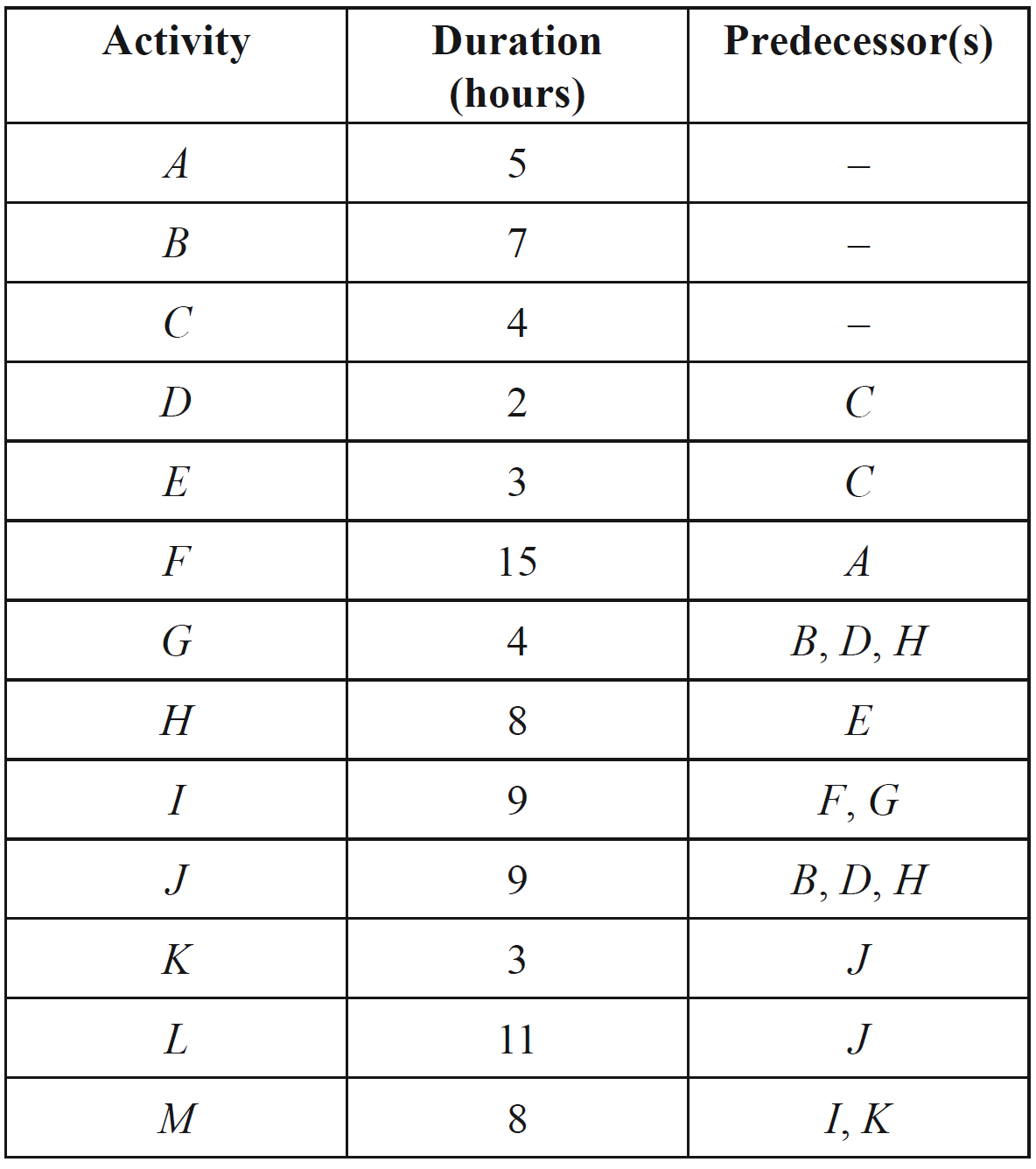
The table below shows the 12 activities that need to be completed for the renovation project.

It also shows the earliest start time (EST), the duration, and the immediate predecessors for the activities.

The immediate predecessor(s) for activity $I$ and the EST for activity $J$ are missing.

\begin{array} {|c|c|c|}
\hline
\quad \textbf{Activity} \quad & \quad\quad\textbf{EST} \quad\quad& \quad\textbf{Duration}\quad & \textbf{Immediate} \\
& & & \textbf{predecessor(s)} \\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & 0 & 6 & - \\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & 0 & 4 & - \\
\hline
\rule{0pt}{2.5ex} C \rule[-1ex]{0pt}{0pt} & 6 & 7 & A \\
\hline
\rule{0pt}{2.5ex} D \rule[-1ex]{0pt}{0pt} & 4 & 5 & B \\
\hline
\rule{0pt}{2.5ex} E \rule[-1ex]{0pt}{0pt} & 4 & 10 & B \\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & 13 & 4 & C \\
\hline
\rule{0pt}{2.5ex} G \rule[-1ex]{0pt}{0pt} & 9 & 3 & D \\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & 9 & 7 & D \\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & 13 & 6 & - \\
\hline
\rule{0pt}{2.5ex} J \rule[-1ex]{0pt}{0pt} & - & 6 & E, H \\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & 19 & 4 & F, I \\
\hline
\rule{0pt}{2.5ex} L \rule[-1ex]{0pt}{0pt} & 23 & 1 & J, K \\
\hline
\end{array}

Write down the immediate predecessor(s) for activity $I$. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
What is the earliest start time, in days, for activity $J$ ? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
How many activities have a float time of zero? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

The managers of the project are able to reduce the time, in days, of six activities.

These reductions will result in an increase in the cost of completing the activity.

The maximum decrease in time of any activity is two days.

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Activity} \rule[-1ex]{0pt}{0pt} & \quad \quad A \quad \quad & \quad \quad B \quad \quad& \quad \quad F \quad \quad & \quad \quad H \quad \quad & \quad \quad I \quad \quad & \quad \quad K \quad \quad \\
\hline
\rule{0pt}{2.5ex} \textbf{Daily cost (\$)} \rule[-1ex]{0pt}{0pt} & 1500 & 2000 & 2500 & 1000 & 1500 & 3000 \\
\hline
\end{array}

If activities $A$ and $B$ have their completion time reduced by two days each, the overall completion time of the project will be reduced.
What will be the maximum reduction time, in days? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
The managers of the project have a maximum budget of $15 000 to reduce the time for several activities to produce the maximum reduction in the project's overall completion time.
Complete the table below, showing the reductions in individual activity completion times that would achieve the earliest completion time within the $ 15 000 budget. (1 mark)

--- 0 WORK AREA LINES (style=lined) ---

\begin{array} {|c|c|}
\hline
\quad\textbf{Activity} \quad & \textbf{Reduction in completion time} \\
& \textbf{(0, 1 or 2 days)}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & \\
\hline
\end{array}

Show Answers Only

a. $\text{Immediate predecessors of}\ I:\ C, G$

b. $\text{EST}(J) = 4+5+7 = 16\ \text{days}$

c. $\text{5 activities have a float time of zero.}$

d. $\text{Maximum reduction time = 2 days}$

\begin{array} {|c|c|}
\hline
\quad\textbf{Activity} \quad & \textbf{Reduction in completion time} \\
& \textbf{(0, 1 or 2 days)}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & 0\\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & 1\\
\hline
\end{array}

Show Worked Solution

a. $\text{Immediate predecessors of}\ I:\ C, G$

$\text{Dummy activity before activity}\ C\ \text{does not effect this.}$

b. $\text{Scan network:}$

$\text{EST}(J) = 4+5+7 = 16\ \text{days}$

c. $\text{Critical Path:}\ A\ C\ I\ K\ L$

$\text{Activities on the critical path have a float time of zero.}$

$\Rightarrow \ \text{5 activities have a float time of zero.}$

d. $\text{If activities}\ A\ \text{and}\ B\ \text{are reduced by 2 days,}$

$\text{the critical path remains:}\ A\ C\ I\ K\ L\ \text{(22 days)}$

$\text{Maximum reduction time = 2 days}$

♦♦ Mean mark (c) 35%.
♦♦ Mean mark (d) 33%.

\begin{array} {|c|c|}
\hline
\quad\textbf{Activity} \quad & \textbf{Reduction in completion time} \\
& \textbf{(0, 1 or 2 days)}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & 0\\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & 1\\
\hline
\end{array}

♦♦♦ Mean mark (e) 9%.

Networks, GEN1 2022 VCAA 7-8 MC

A project involves 11 activities, $A$ to $K$.

The table below shows the earliest start time and duration, in days, for each activity.

The immediate predecessor(s) of each activity is also shown.

\begin{array} {|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ \textbf{Activity}\ \ & \textbf{Earliest} & \ \ \textbf{Duration}\ \ & \textbf{Immediate}\\
& \textbf{start time} \rule[-1ex]{0pt}{0pt} & &\textbf{predecessor}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & \text{0} & \text{6} & \text{-}\\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & \text{0} & \text{7} & \text{-}\\
\hline
\rule{0pt}{2.5ex} C \rule[-1ex]{0pt}{0pt} & \text{6} & \text{10} & A\\
\hline
\rule{0pt}{2.5ex} D \rule[-1ex]{0pt}{0pt} & \text{6} & \text{7} & A\\
\hline
\rule{0pt}{2.5ex} E \rule[-1ex]{0pt}{0pt} & \text{7} & \text{8} & B\\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & \text{15} & \text{2} & D,\ E\\
\hline
\rule{0pt}{2.5ex} G \rule[-1ex]{0pt}{0pt} & \text{15} & \text{2} & E\\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & \text{17} & \text{3} & G\\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & \text{20} & \text{6} & C,\ F,\ H\\
\hline
\rule{0pt}{2.5ex} J \rule[-1ex]{0pt}{0pt} & \text{17} & \text{5} & G\\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & \text{26} & \text{2} & I,\ J\\
\hline
\end{array}

Question 7

A directed network for this project will require a dummy activity.

The dummy activity will be drawn from the end of

activity $A$ to the start of activity $D$.
activity $E$ to the start of activity $F$.
activity $F$ to the start of activity $I$.
activity $G$ to the start of activity $H$.
activity $I$ to the start of activity $J$.

Question 8

When this project is completed in the minimum time, the sum of all the float times, in days, will be

Show Answers Only

$\text{Question 7:}\ B$

$\text{Question 8:}\ D$

Show Worked Solution

$\text{Question 7}$

Draw network from table:

→ $F$ starts after completion of both $D$ and $E$.

→ $G$ starts after activity $E$ only.

$\Rightarrow B$

♦ Mean mark (Q7) 49%.

$\text{Question 8}$

Scanning forwards and backwards on network diagram:

→ The critical path is $B E G H I K$

→ Float times occur at all points not on the critical path.

$\text{Total Float Times}$	$= A + C + D + F + J$
	$= 4 + 4 + 5 + 3 + 4$
	$= 20$

$\Rightarrow D$

♦♦ Mean mark (Q8) 34%.

NETWORKS, FUR2 2020 VCAA 5

The Sunny Coast cricket clubroom is undergoing a major works project.

This project involves nine activities: `A` to `I`.

The table below shows the earliest start time (EST) and duration, in months, for each activity.

The immediate predecessor(s) is also shown.

The duration for activity `C` is missing.

The information in the table above can be used to complete a directed network.

This network will require a dummy activity.

Complete the following sentence by filling in the boxes provided. (1 mark)

This dummy activity could be drawn as a directed edge from the end of activity

the start of activity

What is the duration, in months, of activity `C`? (1 mark)
Name the four activities that have a float time. (1 mark)
The project is to be crashed by reducing the completion time of one activity only.

What is the minimum time, in months, that the project can be completed in? (1 mark)

Show Answers Only

`B\ text{to the start of activity}\ C.`
`text{2 months}`
`A, E, F, H`
`text{17 months}`

Show Worked Solution

a. `B\ text{to the start of activity}\ C.`

♦♦ Mean mark part (a) 26%.

b. `text{Sketch network diagram.}`

♦ Mean mark part (b) 49%.

`text{Duration of Activity C = 2 months}`

c. `text{Critical path:}\ BCDGI`

♦♦ Mean mark part (c) 23%.

`text{Activities with a float time are activities}`

`text{not on critical path.}`

`:. \ text{Four activities are:}\ \ A, E, F, H`

d. `text{Completion time of}\ BCDGI = 20\ text{months}`

♦♦♦ Mean mark part (d) 12%.

`text{Reduce the completion of}\ B\ text{by 3 months to create}`

`text{a new minimum completion time of 17 months.}`

NETWORKS, FUR2-NHT 2019 VCAA 2

The construction of the new reptile exhibit is a project involving nine activities, `A` to `I`.

The directed network below shows these activities and their completion times in weeks.

Which activities have more than one immediate predecessor? (1 mark)
Write down the critical path for this project. (1 mark)
What is the latest start time, in weeks, for activity `B`? (1 mark)

Show Answers Only

`D, G and I`
`text(See Worked Solutions)`
`2\ text(weeks)`

Show Worked Solution

a. `D, G and I`

b. `text(Scanning forwards and backwards:)`

`text(Critical Path:)\ ACDFGI`

c.	`text{LST (activity}\ B text{)}`	`= 7 – 5`
		`= 2\ text(weeks)`

NETWORKS, FUR2 2019 VCAA 3

Fencedale High School is planning to renovate its gymnasium.

This project involves 12 activities, `A` to `L`.

The directed network below shows these activities and their completion times, in weeks.

The minimum completion time for the project is 35 weeks.

How many activities are on the critical path? (1 mark)
Determine the latest start time of activity `E`. (1 mark)
Which activity has the longest float time? (1 mark)

It is possible to reduce the completion time for activities `C, D, G, H` and `K` by employing more workers.

The completion time for each of these five activities can be reduced by a maximum of two weeks.

What is the minimum time, in weeks, that the renovation project could take? (1 mark)
The reduction in completion time for each of these five activities will incur an additional cost to the school.

The table below shows the five activities that can have their completion times reduced and the associated weekly cost, in dollars.


Activity Weekly cost ($)

`C` 3000

`D` 2000

`G` 2500

`H` 1000

`K` 4000


The completion time for each of these five activities can be reduced by a maximum of two weeks.



Fencedale High School requires the overall completion time for the renovation project to be reduced by four weeks at minimum cost.

Complete the table below, showing the reductions in individual activity completion times that would achieve this. (2 marks)


Activity
Reduction in completion time
(0, 1 or 2 weeks)

`C`

`D`

`G`

`H`

`K`

Show Answers Only

`8\ text(activities)`
`12\ text(weeks)`
`text(Activity)\ J`
`29\ text(weeks)`
Activity
Reduction in completion time
(0, 1 or 2 weeks)

`C` 0

`D` 1

`G` 2

`H` 1

`K` 1

Show Worked Solution

a. `text(Scanning forwards and backwards:)`

`text(Crirical path:)\ ABDFGIKL`

`:. 8\ text(activities)`

b. `text(LST for activity)\ E = 12\ text{weeks (i.e. start of 13th week)}`

c. `text(Consider float times of all activities not on critical path.)`

`J-5, H-1, E-1, C-1`

`:.\ text(Activity)\ J\ text(has the largest float time.)`

d. `text(Critical path after reducing)\ CDGHK\ text(by 2 weeks is)`

`ABDFGIKL.`

`:.\ text(Minimum time)`	`= 2 + 4 + 7 + 1 + 2 + 2 + 5 + 6`
	`= 29\ text(weeks)`

e. `text(Reduce cheapest activities on the critical path by 1 week)`

`↓ 1 =>\ text(Activity)\ D\ text(and)\ G`

`text{Possibilities for reducing by a further week (choose 2)}`

`C and D:\ text(cost $5000)\ \ text{(too expensive)}`

`G and H:\ text(cost $3500)\ \ text{(yes)}`

`K:\ text(cost $4000)\ \ text{(yes)}`

	Activity	Reduction in completion time (0, 1 or 2 weeks)
	`C`	0
	`D`	1
	`G`	2
	`H`	1
	`K`	1

NETWORKS, FUR1 2019 VCAA 8 MC

The directed network below shows the sequence of activities, `A` to `S`, that is required to complete a manufacturing process.

The time taken to complete each activity, in hours, is also shown.

The number of activities that have a float time of 10 hours is

Show Answers Only

`B`

Show Worked Solution

`text(Scanning forwards then backwards:)`

`:.\ text(Activities with a float time of 10 hours = 1)`

`=> B`

NETWORKS, FUR2 2018 VCAA 3

At the Zenith Post Office all computer systems are to be upgraded.

This project involves 10 activities, `A` to `J`.

The directed network below shows these activities and their completion times, in hours.

Determine the earliest starting time, in hours, for activity `I`. (1 mark)
The minimum completion time for the project is 15 hours.

Write down the critical path. (1 mark)
Two of the activities have a float time of two hours.

Write down these two activities. (1 mark)
For the next upgrade, the same project will be repeated but one extra activity will be added.
This activity has a duration of one hour, an earliest starting time of five hours and a latest starting time of 12 hours.

Complete the following sentence by filling in the boxes provided. (1 mark)

The extra activity could be represented on the network above by a directed edge from the

end of activity

to the start of activity

Show Answers Only

`10\ text(hours)`
`B – E – G – H – J`
`text(Activity)\ A\ text(and)\ C`
`text(end of activity)\ E\ text(to the start of activity)\ J`

Show Worked Solution

a. `text(Longest path to)\ I:`

`B -> E -> G`

`:.\ text(EST for)\ \ I`	`= 2 + 3 + 5`
	`= 10\ text(hours)`

b. `B – E – G – H – J`

c. `text(Scanning forwards and backwards:)`

♦ Mean mark 45%.

`:.\ text(Activity)\ A\ text(and)\ C\ text(have a 2 hour float time.)`

d. `text(end of activity)\ E\ text(to the start of activity)\ J`

♦♦ Mean mark 25%.

`text(By inspection of forward and backward scanning:)`

`text(EST of 5 hours is possible after activity)\ E.`

`text(LST of 12 hours after activity)\ E -> text(edge has weight)`

`text(of 1 and connects to)\ J`

NETWORKS, FUR2 2017 VCAA 4

The rides at the theme park are set up at the beginning of each holiday season.

This project involves activities A to O.

The directed network below shows these activities and their completion times in days.

Write down the two immediate predecessors of activity I. (1 mark)
The minimum completion time for the project is 19 days.
1. There are two critical paths. One of the critical paths is A–E–J–L–N.
  
  Write down the other critical path. (1 mark)
2. Determine the float time, in days, for activity F. (1 mark)
The project could finish earlier if some activities were crashed.

Six activities, B, D, G, I, J and L, can all be reduced by one day.

The cost of this crashing is $1000 per activity.
1. What is the minimum number of days in which the project could now be completed? (1 mark)
2. What is the minimum cost of completing the project in this time? (1 mark)

Show Answers Only

a. `D\ text(and)\ E`

b.i. `A E I L N`

b.ii. `6\ text(days)`

c.i. `17`

c.ii. `$4000`

Show Worked Solution

a. `D\ text(and)\ E\ (text(note the dummy is not an activity.))`

b.i. `A E I L N`

♦♦ Mean mark part (b)(i) 44% and part (b)(ii) 28%.

b.ii.	`text(Float time)`	`= 19 – (2 + 3 + 3 + 3 + 2)`
		`= 6\ text(days)`

c.i. `text(Reduce activities:)\ I, J, L\ \ (text(on critical path))`

♦♦ Mean mark part (c)(i) 35%.

`text(New critical path)\ \ A C G N\ \ text(takes 18 days.)`

`:. text(Reduce activity)\ G\ text(also.)`

`text(⇒ this critical path reduces to 17 days.)`

`text(⇒ Minimum Days = 17)`

c.ii. `text(Minimum time requires crashing)\ \ I, J, L\ text(and)\ G`

♦♦♦ Mean mark part (c)(ii) 15%.

`:.\ text(Minimum Cost)`	`= 4 xx 1000`
	`= $4000`

NETWORKS, FUR2 2016 VCAA 3

A new skateboard park is to be built in Beachton.

This project involves 13 activities, `A` to `M`.

The directed network below shows these activities and their completion times in days.

Determine the earliest start time for activity `M`. (1 mark)
The minimum completion time for the skateboard park is 15 days.

Write down the critical path for this project. (1 mark)
Which activity has a float time of two days? (1 mark)
The completion times for activities `E, F, G, I` and `J` can each be reduced by one day.

The cost of reducing the completion time by one day for these activities is shown in the table below.

What is the minimum cost to complete the project in the shortest time possible? (1 mark)
The original skateboard park project from part (a), before the reduction of time in any activity, will be repeated at another town named Campville, but with the addition of one extra activity.

The new activity, `N`, will take six days to complete and has a float time of one day.

Activity `N` will finish at the same time as the project.
1. Add activity `N` to the network below. (1 mark)
2. What is the latest start time for activity `N`? (1 mark)

Show Answers Only

`11\ text(days)`
`AEIK`
`text(Activity)\ H`
`text(Minimum cost of $2000 when activity)\ I\ text(is reduced by 1 day.)`
2. `9\ text(days from the start)`

Show Worked Solution

a.	`text(EST)`	`= 1 + 4 + 6`
		`= 11\ text(days)`

b. `text(Critical Path:)\ AEIK`

♦♦ Mean mark part (c) 37%, part (d) 21%.
MARKER’S COMMENT: In part (d), `ADK` cannot be crashed, therefore shortest duration is 14 days. Activity `I` is cheapest to reduce.

c. `text(Activity)\ H`

d. `text(Minimum days to complete is 14 days by reducing)`

`text(either)\ E\ text(or)\ I\ text(by 1 day.)`

`:. text(Minimum cost of $2000 when activity)\ I\ text(is reduced)`

`text(by 1 day.)`

e.i.

♦♦ Mean mark part (e)(i) 21%, (e)(ii) 27%.
MARKER’S COMMENT: In (e)(ii), activity `N` must have an arrow on it.

e.ii.	`text(LST)`	`=\ text(critical path time − 6 days)`
		`= 15 – 6`
		`= 9\ text(days from the start.)`

NETWORKS, FUR2 2006 VCAA 3

The five musicians are to record an album. This will involve nine activities.

The activities and their immediate predecessors are shown in the following table.

The duration of each activity is not yet known.

Use the information in the table above to complete the network below by including activities `G`, `H` and `I`. (2 marks)

There is only one critical path for this project.

How many non-critical activities are there? (1 mark)

The following table gives the earliest start times (EST) and latest start times (LST) for three of the activities only. All times are in hours.

Write down the critical path for this project. (1 mark)

The minimum time required for this project to be completed is 19 hours.

What is the duration of activity `I`? (1 mark)

The duration of activity `C` is 3 hours.

Determine the maximum combined duration of activities `F` and `H`. (1 mark)

Show Answers Only

`5`
`B − E − G − I`
`text(7 hours)`
`text(8 hours)`

Show Worked Solution

b. `text(Possible critical paths are,)`

`ADGI, BEGI\ text(or)\ CFHI`

`:.\ text(Non-critical activities)`

`= 9 – 4 = 5`

c. `text(Critical activities have zero slack time.)`

♦ Mean mark of parts (c)-(e) (combined) was 36%.

`:. A\ text(and)\ C\ text(are non-critical.)`

`:. B − E − G − I\ \ text(is the critical path.)`

d.	`text(Duration of)\ \ I`	`= 19 – 12`
		`= 7\ text(hours)`

e. `text(Maximum time for)\ F\ text(and)\ H`

`=\ text(LST of)\ I – text(duration)\ C – text(slack time of)\ C`

`= 12 – 3 – 1`

`= 8\ text(hours)`

NETWORKS, FUR2 2007 VCAA 4

A community centre is to be built on the new housing estate.

Nine activities have been identified for this building project.

The directed network below shows the activities and their completion times in weeks.

Determine the minimum time, in weeks, to complete this project. (1 mark)
Determine the slack time, in weeks, for activity `D`. (2 marks)

The builders of the community centre are able to speed up the project.

Some of the activities can be reduced in time at an additional cost.

The activities that can be reduced in time are `A`, `C`, `E`, `F` and `G`.

Which of these activities, if reduced in time individually, would not result in an earlier completion of the project? (1 mark)

The owner of the estate is prepared to pay the additional cost to achieve early completion.

The cost of reducing the time of each activity is $5000 per week.

The maximum reduction in time for each one of the five activities, `A`, `C`, `E`, `F`, `G`, is 2 weeks.

Determine the minimum time, in weeks, for the project to be completed now that certain activities can be reduced in time. (1 mark)
Determine the minimum additional cost of completing the project in this reduced time. (1 mark)

Show Answers Only

`19\ text(weeks)`
`5\ text(weeks)`
`A, E, G`
`text(15 weeks)`
`$25\ 000`

Show Worked Solution

a. `B-C-F-H-I\ \ text(is the critical path.)`

♦ Mean mark of all parts (combined) 40%.

`:.\ text(Minimum time)`	`= 4 + 3 + 4 + 2 + 6`
	`= 19\ text(weeks)`

b.	`text(EST of)\ D`	`= 4`
	`text(LST of)\ D`	`= 9`

`:.\ text(Slack time of)\ D`	`= 9 – 4`
	`= 5\ text(weeks)`

c. `A, E,\ text(and)\ G\ text(are not currently on)`

`text(the critical path, therefore crashing)`

`text(them will not affect the completion)`

`text(time.)`

d. `text(Reduce)\ C\ text(and)\ F\ text(by 2 weeks.)`

`text(However, a new critical path)`

`B − E − H − I\ text(takes 16 weeks.)`

`:.\ text(Also reduce)\ E\ text(by 1 week.)`

`:.\ text(Minimum time = 5 weeks)`

e.	`text(Additional cost)`	`= 5 xx $5000`
		`= $25\ 000`

NETWORKS, FUR2 2013 VCAA 2

A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.

Activity `G` is missing from the network diagram for this project, which is shown below.

Complete the network diagram above by inserting activity `G`. (1 mark)
Determine the earliest starting time of activity `H`. (1 mark)
Given that activity `G` is not on the critical path
1. write down the activities that are on the critical path in the order that they are completed (1 mark)
2. find the latest starting time for activity `D`. (1 mark)
Consider the following statement.
‘If just one of the activities in this project is crashed by one hour, then the minimum time to complete the entire project will be reduced by one hour.’

Explain the circumstances under which this statement will be true for this project. (1 mark)
Assume activity `F` is crashed by two hours.
What will be the minimum completion time for the project? (1 mark)

Show Answers Only

`7\ text(hours)`
1. `A − F − I − M`
2. `14\ text(hours)`
`text(The statement will only be true if the crashed activity)`
`text(is on the critical path)\ \ A − F − I − M.`
`text(36 hours)`

Show Worked Solution

b.	`text(EST of)\ H`	`= 4 + 3`
		`= 7\ text(hours)`

c.i. `A − F − I − M`

♦♦ Mean mark of parts (c)-(e) (combined) was 40%.

c.ii.

`G\ text(precedes)\ I`

`:. text(LST of)\ G = 20 – 4 = 16\ text(hours)`

`:. text(LST of)\ D = 16 – 2 = 14\ text(hours)`

d. `text(The statement will only be true if the crashed activity)`

MARKER’S COMMENT: Most students struggled with part (d).

`text(is on the critical path)\ \ A − F − I − M.`

e. `A − F − I − M\ text(is 37 hours.)`

`text(If)\ F\ text(is crashed by 2 hours, the new)`

`text(new critical path is)`

`C − E − H − G − I − M\ text{(36 hours)}`

`:.\ text(Minimum completion time = 36 hours)`

NETWORKS, FUR2 2014 VCAA 4

To restore a vintage train, 13 activities need to be completed.

The network below shows these 13 activities and their completion times in hours.

Determine the earliest starting time of activity `F`. (1 mark)

The minimum time in which all 13 activities can be completed is 21 hours.

What is the latest starting time of activity `L`? (1 mark)
What is the float time of activity `J`? (1 mark)

Just before they started restoring the train, the members of the club needed to add another activity, `X`, to the project.

Activity `X` will take seven hours to complete.

Activity `X` has no predecessors, but must be completed before activity `G` starts.

What is the latest starting time of activity `X` if it is not to increase the minimum completion time of the project? (1 mark)

Activity `A` can be crashed by up to four hours at an additional cost of $90 per our.

This may reduce the minimum completion time for the project, including activity `X`.

Determine the least cost of crashing activity `A` to give the greatest reduction in the minimum completion time of the project. (1 mark)

Show Answers Only

`text(7 hours)`
`text(18 hours)`
`text(2 hours)`
`text(4 hours)`
`$270`

Show Worked Solution

a. `5 + 2 = 7\ text(hours)`

♦ Mean mark for all parts (combined) was 42%.

b. `text(Latest starting time of)\ L`

`= text(Length of critical path – duration of)\ L`

`= 21 – 3`

`= 18\ text(hours)`

c. `text(Float time of)\ J`

`=\ text(LST – EST)`

`= 13 – 11`

`= 2\ text(hours)`

d. `X\ text(precedes)\ G`

`text(EST of)\ G = 11`

`:. text(LST of)\ X = 11`

`text(EST)\ text(of)\ X`

`= text(LST of)\ X – text(duration of)\ X`

`= 11 – 7`

`= 4\ text(hours)`

e. `text(Longer paths are)`

`A – C – G – K = 21\ text{hours (critical path)}`

`A – D – E – H – K = 20\ text(hours)`

`A – D – F – J – M = 19\ text(hours)`

`A – D – E – I – M = 18\ text(hours)`

`B – E – H – K = 18\ text(hours)`

`B – F – J – M = 17\ text(hours)`

`:.\ text(Reduce)\ \ A – C – G – K\ \ text(by 3 hours to get)`

`text{to 18 hours (equals}\ \ B – E – H – K)`

`:.\ text(Least cost)`	`= 3 xx 90`
	`= $270`

NETWORKS, FUR2 2015 VCAA 3

Nine activities are needed to prepare a daily delivery of groceries from the factory to the towns.

The duration, in minutes, earliest starting time (EST) and immediate predecessors for these activities are shown in the table below.

The directed network that shows these activities is shown below.

All nine of these activities can be completed in a minimum time of 26 minutes.

What is the EST of activity `D`? (1 mark)
What is the latest starting time (LST) of activity `D`? (1 mark)
Given that the EST of activity `I` is 22 minutes, what is the duration of activity `H`? (1 mark)
Write down, in order, the activities on the critical path. (1 mark)
Activities `C` and `D` can only be completed by either Cassie or Donna.

One Monday, Donna is sick and both activities `C` and `D` must be completed by Cassie. Cassie must complete one of these activities before starting the other.

What is the least effect of this on the usual minimum preparation time for the delivery of groceries from the factory to the five towns? (1 mark)
Every Friday, a special delivery to the five towns includes fresh seafood. This causes a slight change to activity `G`, which then cannot start until activity `F`
has been completed.
1. On the directed graph below, show this change without duplicating any activity. (1 mark)
2. What effect does the inclusion of seafood on Fridays have on the usual minimum preparation time for deliveries from the factory to the five towns? (1 mark)

Show Answers Only

`text(3 minutes)`
`text(4 minutes)`
`text(3 minutes)`
`A – C – F – H – I`
`text(The critical path is increased by)`
`text(7 minutes to 33 minutes.)`
2. `text(The critical path is increased by)`
  `text(2 minutes to 28 minutes.)`

Show Worked Solution

a. `text(3 minutes)`

b. `text(4 minutes)`

c. `text(3 minutes)`

d. `A – C – F – H – I`

e. `text(The critical path is increased by 7 minutes)`

`text(to 33 minutes.)`

f.i.

f.ii. `text(The critical path is increased by 2 minutes)`

`text(to 28 minutes.)`

NETWORKS, FUR2 2012 VCAA 2

Thirteen activities must be completed before the produce grown on a farm can be harvested.

The directed network below shows these activities and their completion times in days.

Determine the earliest starting time, in days, for activity `E`. (1 mark)
A dummy activity starts at the end of activity `B`.

Explain why this dummy activity is used on the network diagram. (1 mark)
Determine the earliest starting time, in days, for activity `H`. (1 mark)
In order, list the activities on the critical path. (1 mark)
Determine the latest starting time, in days, for activity `J`. (1 mark)

Show Answers Only

`12\ text(days)`
`F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`
`text(have)\ B\ text(and)\ C\ text(as predecessors.)`
`text(S)text(ince there cannot be 2 activities called)\ B,`
`text{a dummy activity is drawn as an extension of}`
`B\ text(to show that it is also a predecessor of)\ G\ text(and)`
`H\ text{(with zero time).}`
`15\ text(days)`
`A-B-H-I-L-M`
`25\ text(days)`

Show Worked Solution

a.	`text(EST of)\ E`	`= 10 + 2`
		`= 12\ text(days)`

♦ Mean mark of all parts (combined) 47%.

b. `F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`

`text(have)\ B\ text(and)\ C\ text(as predecessors.)`

`text(S)text(ince there cannot be 2 activities called)\ B,`

`text{a dummy activity is drawn as an extension of}`

`B\ text(to show that it is also a predecessor of)\ G\ text(and)`

`H\ text{(with zero time).}`

♦♦ Exact data unavailable but “few students” were able to correctly deal with the dummy activity in this question.

c.	`text(EST of)\ H`	`= 10 + 5`
		`= 15\ text(days)`

d. `text(The critical path is)`

`A-B-H-I-L-M`

e. `text(The shortest time to complete all the activities)`

MARKER’S COMMENT: A correct calculation based on an incorrect critical path in part (d) gained a consequential mark here. Show your working!

`= 10 + 5 + 4 + 3 + 4 + 2`

`= 28\ text(days)`

`:.\ text(LST of)\ J`	`= 28 − 3`
	`= 25\ text(days)`

\(\text{Total Float Times}\)	\(= A + C + D + F + J\)
	\(= 4 + 4 + 5 + 3 + 4\)
	\(= 20\)