An upgrade to the supermarket requires the completion of 11 activities, \(A\) to \(K\). The directed network below shows these activities and their completion time, in weeks. The minimum completion time for the project is 29 weeks. --- 1 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) --- Use the following information to answer parts c-e. A change is made to the order of activities. The table below shows the activities and their new latest starting times in weeks. \begin{array}{|c|c|} A dummy activity is now required in the network. --- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) --- a. \(A, C, H, J\) b. \(\text{Activity E}\) c. d. \(\text{30 weeks}\) e. \($50\,000\) a. \(\text{Critical path: }A, C, H, J\) \(\text{Consider Activity E:}\) \(\text{EST = 11, LST}= 18-4=14\rightarrow\ \text{Float time = 3 weeks}\) \(\therefore\ \text{Activity E can be delayed the longest.}\) c. e. \(\text{Activities that can be reduced:}\) \(-A\ \text{can be reduced by 2 weeks}\) \(-B, D\ \text{can each be reduced by 1 week each}\) \(-H\ \text{can be reduced by 1 week}\) \(\text{Total reduction = 5 weeks}\) \(\Rightarrow \ \text{Minimum payment}=$50\,000\)
\hline
\textbf{Activity} & \textbf{Latest Starting}\\
&\textbf{time} \text{(weeks)}\\
\hline A & 0 \\
\hline B & 2 \\
\hline C & 10 \\
\hline D & 9 \\
\hline E & 13 \\
\hline F & 14 \\
\hline G & 18 \\
\hline H & 17 \\
\hline I & 19 \\
\hline J & 25 \\
\hline K & 22 \\
\hline
\end{array}
b. \(\text{Activity with the largest float time can be delayed the longest.}\)
Networks, GEN2 2023 VCAA 14
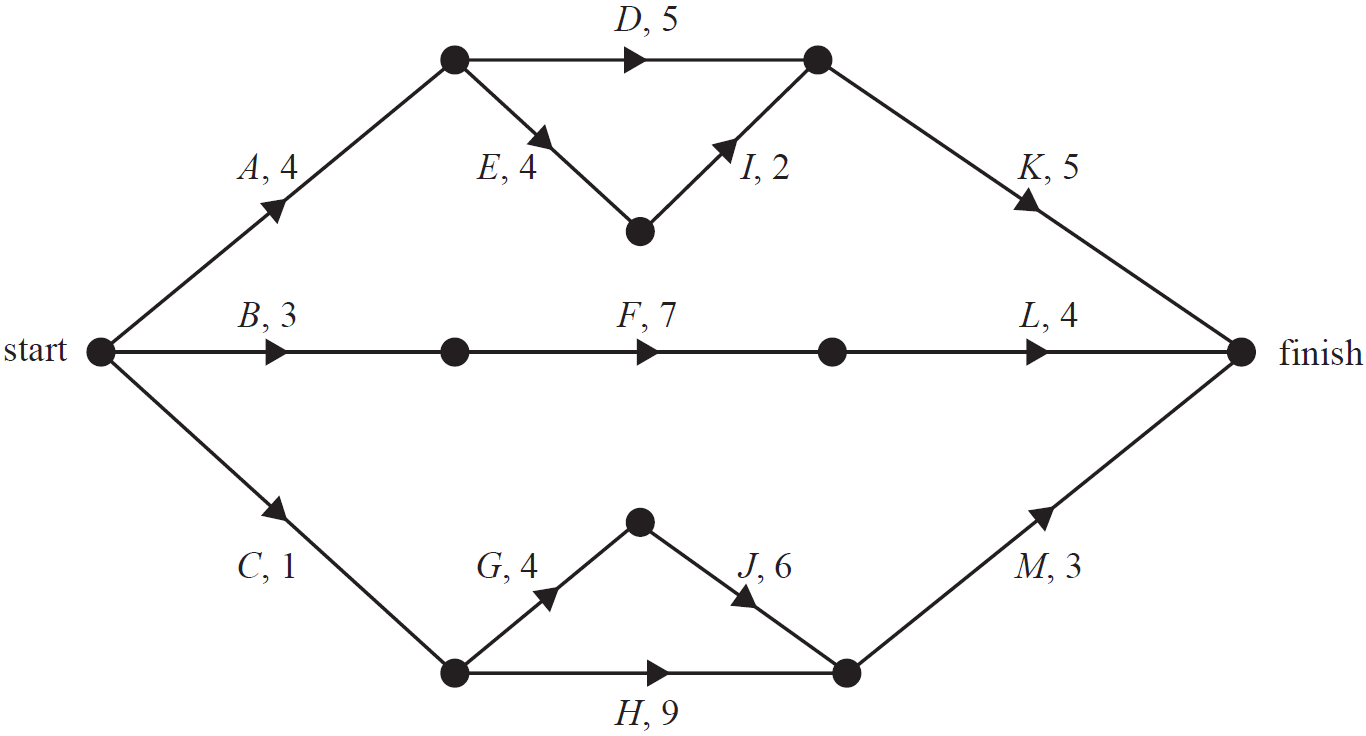
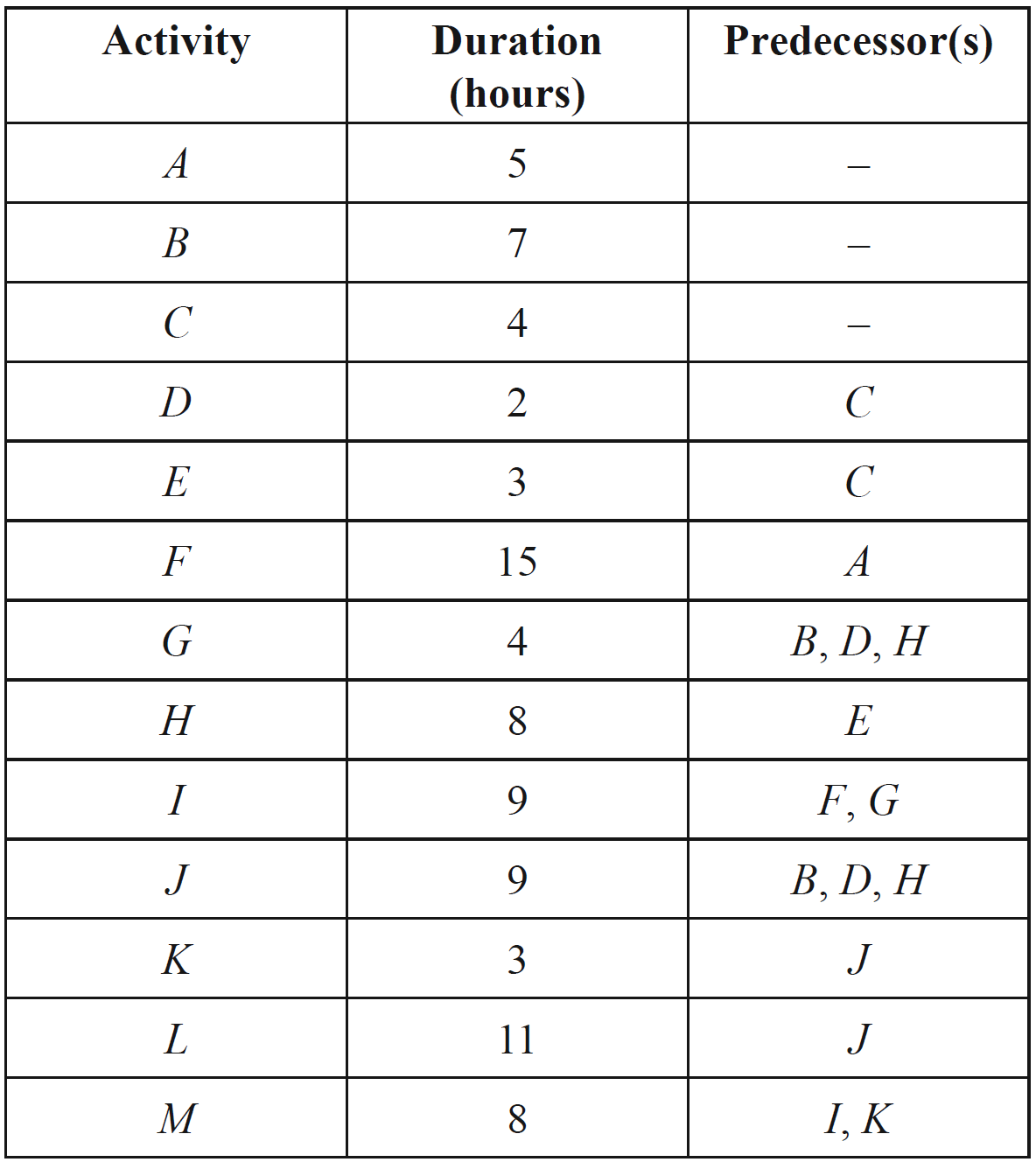
One of the landmarks in state \(A\) requires a renovation project.
This project involves 12 activities, \(A\) to \(L\). The directed network below shows these activities and their completion times, in days.
The table below shows the 12 activities that need to be completed for the renovation project.
It also shows the earliest start time (EST), the duration, and the immediate predecessors for the activities.
The immediate predecessor(s) for activity \(I\) and the EST for activity \(J\) are missing.
\begin{array} {|c|c|c|}
\hline
\quad \textbf{Activity} \quad & \quad\quad\textbf{EST} \quad\quad& \quad\textbf{Duration}\quad & \textbf{Immediate} \\
& & & \textbf{predecessor(s)} \\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & 0 & 6 & - \\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & 0 & 4 & - \\
\hline
\rule{0pt}{2.5ex} C \rule[-1ex]{0pt}{0pt} & 6 & 7 & A \\
\hline
\rule{0pt}{2.5ex} D \rule[-1ex]{0pt}{0pt} & 4 & 5 & B \\
\hline
\rule{0pt}{2.5ex} E \rule[-1ex]{0pt}{0pt} & 4 & 10 & B \\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & 13 & 4 & C \\
\hline
\rule{0pt}{2.5ex} G \rule[-1ex]{0pt}{0pt} & 9 & 3 & D \\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & 9 & 7 & D \\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & 13 & 6 & - \\
\hline
\rule{0pt}{2.5ex} J \rule[-1ex]{0pt}{0pt} & - & 6 & E, H \\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & 19 & 4 & F, I \\
\hline
\rule{0pt}{2.5ex} L \rule[-1ex]{0pt}{0pt} & 23 & 1 & J, K \\
\hline
\end{array}
- Write down the immediate predecessor(s) for activity \(I\). (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- What is the earliest start time, in days, for activity \(J\) ? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- How many activities have a float time of zero? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
The managers of the project are able to reduce the time, in days, of six activities.
These reductions will result in an increase in the cost of completing the activity.
The maximum decrease in time of any activity is two days.
\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Activity} \rule[-1ex]{0pt}{0pt} & \quad A \quad & \quad B \quad& \quad F \quad & \quad H \quad & \quad I \quad & \quad K \quad \\
\hline
\rule{0pt}{2.5ex} \textbf{Daily cost (\$)} \rule[-1ex]{0pt}{0pt} & 1500 & 2000 & 2500 & 1000 & 1500 & 3000 \\
\hline
\end{array}
- If activities \(A\) and \(B\) have their completion time reduced by two days each, the overall completion time of the project will be reduced.
- What will be the maximum reduction time, in days? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- The managers of the project have a maximum budget of $15 000 to reduce the time for several activities to produce the maximum reduction in the project's overall completion time.
- Complete the table below, showing the reductions in individual activity completion times that would achieve the earliest completion time within the $ 15 000 budget. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
\begin{array} {|c|c|}
\hline
\quad\textbf{Activity} \quad & \textbf{Reduction in completion time} \\
& \textbf{(0, 1 or 2 days)}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & \\
\hline
\end{array}
Show Worked Solution
a. \(\text{Immediate predecessors of}\ I:\ C, G\)
\(\text{Dummy activity before activity}\ C\ \text{does not effect this.}\)
b. \(\text{Scan network:}\)
\(\text{EST}(J) = 4+5+7 = 16\ \text{days}\)
c. \(\text{Critical Path:}\ A\ C\ I\ K\ L\)
\(\text{Activities on the critical path have a float time of zero.}\)
\(\Rightarrow \ \text{5 activities have a float time of zero.}\)
d. \(\text{If activities}\ A\ \text{and}\ B\ \text{are reduced by 2 days,}\)
\(\text{the critical path remains:}\ A\ C\ I\ K\ L\ \text{(22 days)}\)
\(\text{Maximum reduction time = 2 days}\)
♦♦ Mean mark (c) 35%.
♦♦ Mean mark (d) 33%.
♦♦ Mean mark (d) 33%.
e.
\begin{array} {|c|c|}
\hline
\quad\textbf{Activity} \quad & \textbf{Reduction in completion time} \\
& \textbf{(0, 1 or 2 days)}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & 0\\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & 2\\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & 1\\
\hline
\end{array}
♦♦♦ Mean mark (e) 9%.
NETWORKS, FUR2 2020 VCAA 5
The Sunny Coast cricket clubroom is undergoing a major works project.
This project involves nine activities: `A` to `I`.
The table below shows the earliest start time (EST) and duration, in months, for each activity.
The immediate predecessor(s) is also shown.
The duration for activity `C` is missing.
The information in the table above can be used to complete a directed network.
This network will require a dummy activity.
- Complete the following sentence by filling in the boxes provided. (1 mark)
This dummy activity could be drawn as a directed edge from the end of activity to the start of activity--- 0 WORK AREA LINES (style=lined) ---
- What is the duration, in months, of activity `C`? (1 mark)
--- 5 WORK AREA LINES (style=blank) ---
--- 2 WORK AREA LINES (style=lined) ---
- Name the four activities that have a float time. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- The project is to be crashed by reducing the completion time of one activity only.
What is the minimum time, in months, that the project can be completed in? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
Show Worked Solution
a. `B\ text{to the start of activity}\ C.`
♦♦ Mean mark part (a) 26%.
b. `text{Sketch network diagram.}`
♦ Mean mark part (b) 49%.
`text{Duration of Activity C = 2 months}`
c. `text{Critical path:}\ BCDGI`
♦♦ Mean mark part (c) 23%.
`text{Activities with a float time are activities}`
`text{not on critical path.}`
`:. \ text{Four activities are:}\ \ A, E, F, H`
d. `text{Completion time of}\ BCDGI = 20\ text{months}`
♦♦♦ Mean mark part (d) 12%.
`text{Reduce the completion of}\ B\ text{by 3 months to create}`
`text{a new minimum completion time of 17 months.}`
NETWORKS, FUR2 2021 VCAA 4
Roadworks planned by the local council require 13 activities to be completed.
The network below shows these 13 activities and their completion times in weeks.
- What is the earliest start time, in weeks, of activity `K`? (1 mark)
--- 5 WORK AREA LINES (style=lined) ---
- How many of these activities have zero float time? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- It is possible to reduce the completion time for activities `A, E, F, L` and `K`.
- The reduction in completion time for each of these five activities will incur an additional cost.
- The table below shows the five activities that can have their completion time reduced and the associated weekly cost, in dollars.
- The completion time for each these five activities can be reduced by a maximum of two weeks.
- The overall completion time for the roadworks can be reduced to 16 weeks.
- What is the minimum cost, in dollars, of this change in completion time? (1 mark)
--- 12 WORK AREA LINES (style=lined) ---
Show Worked Solution
a. `text{Scan forwards:}`
`EST \ (text{activity} \ K)`
`= A \ E \ J`
`= 6 + 5 + 3`
`= 14 \ text{weeks}`
b. `text{Scan backwards:}`
`text{Critical paths:}\ ADGLM\ text(and)\ AEHLM`
`:. \ text{7 activities have no float time:} \ ADEGHLM`
c. `text{There are 9 possible paths}`
`ADGLM\ (19), AEHLM\ (19) , AEIM\ (14)`
`AEJK\ (17), BCEIM \ (13), BCEJK\ (16)`
`BCEHLM\ (18), BCDGLM \ (18), BFK (11)`
`text{Consider the 5 paths with completions over 16 weeks}`
` to \ text{all contain}\ A\ text{or}\ L \ text{or both.}`
`text{Consider} \ ADGLM, AEHLM \ (text{contains both} \ A\ text{and} \ L )`
`to \ text{reduce} \ L xx 2 \ , A xx 1 \ text{to reach 16 weeks}`
`to \ text{cheaper than} \ L xx 1 \ , \ A xx 2`
`text{Consider} \ BCEHLM , BCDGLM\ (text{both contain} \ L \ text{only})`
`to \ text{reduce} \ L xx 2 \ text{to reach 16 weeks}`
`text{Consider} \ AEJK \ ( text{contains} \ A \ text{only} )`
`to \ text{reduce} \ A xx 1 \ text{reach 16 weeks}.`
`:. \ text{Minimum cost to reduce time to 16 weeks}`
`= 2 xx 120\ 000 + 1 xx 140\ 000`
`= $ 380\ 000`
NETWORKS, FUR1 2020 VCAA 10 MC
The directed network below shows the sequence of activities, `A` to `I`, that is required to complete an office renovation.
The time taken to complete each activity, in weeks, is also shown.
The project manager would like to complete the office renovation in less time.
The project manager asks all the workers assigned to activity `H` to also work on activity `F`.
This will reduce the completion time of activity `F` to three weeks.
The workers assigned to activity `H` cannot work on both activity `H` and activity `F` at the same time.
No other activity times will be changed.
This change to the network will result in a change to the completion time of the office renovation.
Which one of the following is correct?
- The completion time will be reduced by one week if activity `F` is completed before activity `H` is started.
- The completion time will be reduced by three weeks if activity `F` is completed before activity `H` is started.
- The completion time will be reduced by one week if activity `H` is completed before activity `F` is started.
- The completion time will be reduced by three weeks if activity `H` is completed before activity `F` is started.
- The completion time will be increased by three weeks if activity `H` is completed before activity `F` is started.
Show Worked Solution
`text{Original forward scan (note}\ F\ text{is 6 origionally but}`
♦♦♦ Mean mark 24%.
`text{is reduced to 3 for the adjusted critical path):}`
`text(Original critical path is:)\ ACEFGI = 2+5+3+6+4+5=25`
`text(If activity)\ F\ text(is completed in 3 weeks, and then)`
`text(activity)\ H\ text(starts, new critical path is:)`
`ACEF\ text{(dummy)}\ HI = 24\ text(weeks)`
`=> A`
NETWORKS, FUR1-NHT 2019 VCAA 8 MC
A landscape gardener is planning the construction of a garden.
This project requires 13 activities, `I` to `U`.
The directed graph below shows each of these activities represented by edges.
The numbers on the edges are the durations of the activities, in days.
The cost of reducing the completion time of any activity in this project is $1000 per day.
The landscape gardener has a maximum of $3000 to spend on reducing the minimum completion time of this project.
The total completion time of the project can be reduced by three days by reducing
- activity `K` by one day and activity `Q` by two days.
- activity `K` by two days and activity `Q` by one day.
- activity `K` by two days and activity `M` by one day.
- activity `K` by one day and activity `M` by two days.
- activity `K` by one day, activity `M` by one day and activity `Q` by one day.
Show Worked Solution
`text(Scanning forwards and backwards.)`
`text(Critical path:)\ KNQTU`
`text(By reducing)\ K\ text(by)\ 2\ text(days and)\ Q\ text(by 1 day, the critical)`
`text(path remains)\ KNQTU\ text{(reduced by 3 days).}`
`=> B`
NETWORKS, FUR2 2019 VCAA 3
Fencedale High School is planning to renovate its gymnasium.
This project involves 12 activities, `A` to `L`.
The directed network below shows these activities and their completion times, in weeks.
The minimum completion time for the project is 35 weeks.
- How many activities are on the critical path? (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Determine the latest start time of activity `E`. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Which activity has the longest float time? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
It is possible to reduce the completion time for activities `C, D, G, H` and `K` by employing more workers.
- The completion time for each of these five activities can be reduced by a maximum of two weeks.
What is the minimum time, in weeks, that the renovation project could take? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- The reduction in completion time for each of these five activities will incur an additional cost to the school.
The table below shows the five activities that can have their completion times reduced and the associated weekly cost, in dollars.
Activity Weekly cost ($) `C` 3000 `D` 2000 `G` 2500 `H` 1000 `K` 4000
The completion time for each of these five activities can be reduced by a maximum of two weeks.Fencedale High School requires the overall completion time for the renovation project to be reduced by four weeks at minimum cost.
Complete the table below, showing the reductions in individual activity completion times that would achieve this. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Activity Reduction in completion time
(0, 1 or 2 weeks)`C` `D` `G` `H` `K`
Show Worked Solution
a. `text(Scanning forwards and backwards:)`
 |
`text(Crirical path:)\ ABDFGIKL`
`:. 8\ text(activities)`
b. `text(LST for activity)\ E = 12\ text{weeks (i.e. start of 13th week)}`
c. `text(Consider float times of all activities not on critical path.)`
`J-5, H-1, E-1, C-1`
`:.\ text(Activity)\ J\ text(has the largest float time.)`
d. `text(Critical path after reducing)\ CDGHK\ text(by 2 weeks is)`
`ABDFGIKL.`
| `:.\ text(Minimum time)` | `= 2 + 4 + 7 + 1 + 2 + 2 + 5 + 6` |
| `= 29\ text(weeks)` |
e. `text(Reduce cheapest activities on the critical path by 1 week)`
`↓ 1 =>\ text(Activity)\ D\ text(and)\ G`
`text{Possibilities for reducing by a further week (choose 2)}`
`C and D:\ text(cost $5000)\ \ text{(too expensive)}`
`G and H:\ text(cost $3500)\ \ text{(yes)}`
`K:\ text(cost $4000)\ \ text{(yes)}`
| Activity | Reduction in completion time (0, 1 or 2 weeks) |
|
| `C` | 0 | |
| `D` | 1 | |
| `G` | 2 | |
| `H` | 1 | |
| `K` | 1 |
NETWORKS, FUR2 2017 VCAA 4
The rides at the theme park are set up at the beginning of each holiday season.
This project involves activities A to O.
The directed network below shows these activities and their completion times in days.
- Write down the two immediate predecessors of activity I. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- The minimum completion time for the project is 19 days.
i. There are two critical paths. One of the critical paths is A–E–J–L–N.
Write down the other critical path. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
ii. Determine the float time, in days, for activity F. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- The project could finish earlier if some activities were crashed.
Six activities, B, D, G, I, J and L, can all be reduced by one day.
The cost of this crashing is $1000 per activity.
i. What is the minimum number of days in which the project could now be completed? (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
ii. What is the minimum cost of completing the project in this time? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
NETWORKS, FUR2 2016 VCAA 3
A new skateboard park is to be built in Beachton.
This project involves 13 activities, `A` to `M`.
The directed network below shows these activities and their completion times in days.
- Determine the earliest start time for activity `M`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- The minimum completion time for the skateboard park is 15 days.
Write down the critical path for this project. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Which activity has a float time of two days? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- The completion times for activities `E, F, G, I` and `J` can each be reduced by one day.
The cost of reducing the completion time by one day for these activities is shown in the table below.
What is the minimum cost to complete the project in the shortest time possible? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- The original skateboard park project from part (a), before the reduction of time in any activity, will be repeated at another town named Campville, but with the addition of one extra activity.
The new activity, `N`, will take six days to complete and has a float time of one day.
Activity `N` will finish at the same time as the project.
i. Add activity `N` to the network below. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
ii. What is the latest start time for activity `N`? (1 mark)--- 3 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
| a. | `text(EST)` | `= 1 + 4 + 6` |
| `= 11\ text(days)` |
b. `text(Critical Path:)\ AEIK`
♦♦ Mean mark part (c) 37%, part (d) 21%.
MARKER’S COMMENT: In part (d), `ADK` cannot be crashed, therefore shortest duration is 14 days. Activity `I` is cheapest to reduce.
MARKER’S COMMENT: In part (d), `ADK` cannot be crashed, therefore shortest duration is 14 days. Activity `I` is cheapest to reduce.
c. `text(Activity)\ H`
d. `text(Minimum days to complete is 14 days by reducing)`
`text(either)\ E\ text(or)\ I\ text(by 1 day.)`
`:. text(Minimum cost of $2000 when activity)\ I\ text(is reduced)`
`text(by 1 day.)`
| e.i. |
|
♦♦ Mean mark part (e)(i) 21%, (e)(ii) 27%.
MARKER’S COMMENT: In (e)(ii), activity `N` must have an arrow on it.
MARKER’S COMMENT: In (e)(ii), activity `N` must have an arrow on it.
| e.ii. | `text(LST)` | `=\ text(critical path time − 6 days)` |
| `= 15-6` | ||
| `= 9\ text(days from the start.)` |
NETWORKS, FUR1 2012 VCAA 8 MC
Eight activities, `A, B, C, D, E, F, G\ text(and)\ H`, must be completed for a project.
The graph above shows these activities and their usual duration in hours.
The duration of each activity can be reduced by one hour.
To complete this project in 16 hours, the minimum number of activities that must be reduced by one hour each is
A. 1
B. 2
C. 3
D. 4
E. 5
NETWORKS, FUR1 2013 VCAA 8 MC
The graph above shows five activities, `A, B, C, D\ text(and)\ E`, that must be completed to finish a project.
The number next to each letter shows the completion time, in hours, for the activity.
Each of the five activities can have its completion time reduced by a maximum of one hour at a cost of $100 per hour.
The least cost to achieve the greatest reduction in the time taken to finish the project is
A. $100
B. $200
C. $300
D. $400
E. $500
NETWORKS, FUR2 2007 VCAA 4
A community centre is to be built on the new housing estate.
Nine activities have been identified for this building project.
The directed network below shows the activities and their completion times in weeks.
- Determine the minimum time, in weeks, to complete this project. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Determine the slack time, in weeks, for activity `D`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
The builders of the community centre are able to speed up the project.
Some of the activities can be reduced in time at an additional cost.
The activities that can be reduced in time are `A`, `C`, `E`, `F` and `G`.
- Which of these activities, if reduced in time individually, would not result in an earlier completion of the project? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
The owner of the estate is prepared to pay the additional cost to achieve early completion.
The cost of reducing the time of each activity is $5000 per week.
The maximum reduction in time for each one of the five activities, `A`, `C`, `E`, `F`, `G`, is 2 weeks.
- Determine the minimum time, in weeks, for the project to be completed now that certain activities can be reduced in time. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- Determine the minimum additional cost of completing the project in this reduced time. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
NETWORKS, FUR2 2013 VCAA 2
A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.
Activity `G` is missing from the network diagram for this project, which is shown below.
- Complete the network diagram above by inserting activity `G`. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
- Determine the earliest starting time of activity `H`. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Given that activity `G` is not on the critical path:
i. Write down the activities that are on the critical path in the order that they are completed. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- ii. Find the latest starting time for activity `D`. (1 mark)
--- 5 WORK AREA LINES (style=lined) ---
- Consider the following statement.
‘If just one of the activities in this project is crashed by one hour, then the minimum time to complete the entire project will be reduced by one hour.’Explain the circumstances under which this statement will be true for this project. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Assume activity `F` is crashed by two hours.
What will be the minimum completion time for the project? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
Show Answers Only
-
- `7\ text(hours)`
- i. `A-F-I-M`
ii. `14\ text(hours)` - `text(The statement will only be true if the crashed activity)`
`text(is on the critical path)\ \ A-F-I-M.` - `text(36 hours)`
Show Worked Solution
| a. |  |
| b. | `text(EST of)\ H` | `= 4 + 3` |
| `= 7\ text(hours)` |
c.i. `A-F-I-M`
♦♦ Mean mark of parts (c)-(e) (combined) was 40%.
| c.ii. |  |
`G\ text(precedes)\ I`
`:. text(LST of)\ G = 20-4 = 16\ text(hours)`
`:. text(LST of)\ D = 16-2 = 14\ text(hours)`
d. `text(The statement will only be true if the crashed activity)`
MARKER’S COMMENT: Most students struggled with part (d).
`text(is on the critical path)\ \ A-F-I-M.`
e. `A-F-I-M\ text(is 37 hours.)`
`text(If)\ F\ text(is crashed by 2 hours, the new)`
`text(new critical path is)`
`C-E-H-G-I-M\ text{(36 hours)}`
`:.\ text(Minimum completion time = 36 hours)`
NETWORKS, FUR2 2009 VCAA 4
A walkway is to be built across the lake.
Eleven activities must be completed for this building project.
The directed network below shows the activities and their completion times in weeks.
- What is the earliest start time for activity `E`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Write down the critical path for this project. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- The project supervisor correctly writes down the float time for each activity that can be delayed and makes a list of these times.
Determine the longest float time, in weeks, on the supervisor’s list. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
A twelfth activity, `L`, with duration three weeks, is to be added without altering the critical path.
Activity `L` has an earliest start time of four weeks and a latest start time of five weeks.
- Draw in activity `L` on the network diagram above. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
- Activity `L` starts, but then takes four weeks longer than originally planned.
Determine the total overall time, in weeks, for the completion of this building project. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
Show Answers Only
- `7`
- `BDFGIK`
- `H\ text(or)\ J\ text(can be delayed for)`
`text(a maximum of 3 weeks.)` -
- `text(25 weeks)`
Show Worked Solution
a. `7\ text(weeks)`
♦ Mean mark of all parts (combined): 44%.
b. `BDFGIK`
c. `H\ text(or)\ J\ text(can be delayed for a maximum)`
`text(of 3 weeks.)`
| d. |  |
e. `text(The new critical path is)\ BLEGIK.`
`L\ text(now takes 7 weeks.)`
`:.\ text(Time for completion)`
`= 4 + 7 + 1 + 5 + 2 + 6`
`= 25\ text(weeks)`
NETWORKS, FUR2 2011 VCAA 3
A section of the Farnham showgrounds has flooded due to a broken water pipe. The public will be stopped from entering the flooded area until repairs are made and the area has been cleaned up.
The table below shows the nine activities that need to be completed in order to repair the water pipe. Also shown are some of the durations, Earliest Start Times (EST) and the immediate predecessors for the activities.
- What is the duration of activity `B`? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- What is the Earliest Start Time (EST) for activity `D`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Once the water has been turned off (Activity `B`), which of the activities `C` to `I` could be delayed without affecting the shortest time to complete all activities? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
It is more complicated to replace the broken water pipe (Activity `E`) than expected. It will now take four hours to complete instead of two hours.
- Determine the shortest time in which activities `A` to `I` can now be completed. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Turning on the water to the showgrounds (Activity `H`) will also take more time than originally expected. It will now take five hours to complete instead of one hour.
- With the increased duration of Activity `H` and Activity `E`, determine the shortest time in which activities `A` to `I` can be completed. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---