SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, GEN2 2024 VCAA 15

An upgrade to the supermarket requires the completion of 11 activities, \(A\) to \(K\).

The directed network below shows these activities and their completion time, in weeks.

The minimum completion time for the project is 29 weeks.
 

 

  1. Write down the critical path.   (1 mark)

  2. Which activity can be delayed for the longest time without affecting the minimum completion time of the project?   (1 mark)

Use the following information to answer parts c-e.

A change is made to the order of activities.

The table below shows the activities and their new latest starting times in weeks.

\begin{array}{|c|c|}
\hline
\textbf{Activity} & \textbf{Latest Starting}\\
&\textbf{time} \text{(weeks)}\\
\hline A & 0 \\
\hline B & 2 \\
\hline C & 10 \\
\hline D & 9 \\
\hline E & 13 \\
\hline F & 14 \\
\hline G & 18 \\
\hline H & 17 \\
\hline I & 19 \\
\hline J & 25 \\
\hline K & 22 \\
\hline
\end{array}

A dummy activity is now required in the network.

  1. On the directed network below, draw a directed edge to represent the dummy activity. Include a label.  (1 mark)

     

  1. What is the new minimum completion time of the project?  (1 mark)
  2. The owners of the supermarket want the project completed earlier.
  3. They will pay to reduce the time of some of the activities.
  4. A reduction in completion time of an activity will incur an additional cost of $10 000 per week.
  5. Activities can be reduced by a maximum of two weeks.
  6. The minimum number of weeks an activity can be reduced to is seven weeks.
  7. What is the minimum amount the owners of the supermarket will have to pay to reduce the completion time of the project as much as possible?   (1 mark)

Show Answers Only

a.    \(A, C, H, J\)

b.    \(\text{Activity E}\)

c.    

d.    \(\text{30 weeks}\)

e.    \($50\,000\)

Show Worked Solution

a.    \(\text{Critical path:  }A, C, H, J\)
 

 
b.    \(\text{Activity with the largest float time can be delayed the longest.}\)

\(\text{Consider Activity E:}\)

\(\text{EST = 11, LST}= 18-4=14\rightarrow\ \text{Float time = 3 weeks}\)

\(\therefore\ \text{Activity E can be delayed the longest.}\)
 

♦♦ Mean mark (b) 34%.

c.    

♦♦♦ Mean mark (c) 10%.

d.    \(\text{New minimum completion time is 30 weeks.}\)
 

♦♦♦ Mean mark (d) 27%.

e.    \(\text{Activities that can be reduced:}\)

\(-A\ \text{can be reduced by 2 weeks}\)

\(-B, D\ \text{can each be reduced by 1 week each}\)

\(-H\ \text{can be reduced by 1 week}\)

\(\text{Total reduction = 5 weeks}\)

\(\Rightarrow \ \text{Minimum payment}=$50\,000\)

♦♦♦ Mean mark (e) 7%.

NETWORKS, FUR2 2018 VCAA 3

At the Zenith Post Office all computer systems are to be upgraded.

This project involves 10 activities, `A` to `J`.

The directed network below shows these activities and their completion times, in hours.
 

  1. Determine the earliest starting time, in hours, for activity `I`.   (1 mark)

  2. The minimum completion time for the project is 15 hours.

     

    Write down the critical path.   (1 mark)

  3. Two of the activities have a float time of two hours.

     

    Write down these two activities.   (1 mark)

  4. For the next upgrade, the same project will be repeated but one extra activity will be added.
    This activity has a duration of one hour, an earliest starting time of five hours and a latest starting time of 12 hours.

     

    Complete the following sentence by filling in the boxes provided.   (1 mark)

     

    The extra activity could be represented on the network above by a directed edge from the

   end of activity   
 
   to the start of activity   
 
Show Answers Only
  1. `10\ text(hours)`
  2. `B-E-G-H-J`
  3.  `text(Activity)\ A\ text(and)\ C`
  4. `text(end of activity)\ E\ text(to the start of activity)\ J`
Show Worked Solution

a.  `text(Longest path to)\ I:`

`B -> E -> G`

`:.\ text(EST for)\ \ I` `= 2 + 3 + 5`
  `= 10\ text(hours)`

 
b.  `B-E-G-H-J`
 

c.  `text(Scanning forwards and backwards:)`

♦ Mean mark 45%.

 


 

`:.\ text(Activity)\ A\ text(and)\ C\ text(have a 2 hour float time.)`
 

d.   `text(end of activity)\ E\ text(to the start of activity)\ J`

♦♦ Mean mark 25%.
 

`text(By inspection of forward and backward scanning:)`

`text(EST of 5 hours is possible after activity)\ E.`

`text(LST of 12 hours after activity)\ E -> text(edge has weight)`

`text(of 1 and connects to)\ J`

NETWORKS, FUR2 2016 VCAA 3

A new skateboard park is to be built in Beachton.

This project involves 13 activities, `A` to `M`.

The directed network below shows these activities and their completion times in days.
 


 

  1. Determine the earliest start time for activity `M`.   (1 mark)

  2. The minimum completion time for the skateboard park is 15 days.

     

    Write down the critical path for this project.   (1 mark)

  3. Which activity has a float time of two days?   (1 mark)

  4. The completion times for activities `E, F, G, I` and `J` can each be reduced by one day.

     

    The cost of reducing the completion time by one day for these activities is shown in the table below.
     

     

       

     

    What is the minimum cost to complete the project in the shortest time possible?   (1 mark)

  5. The original skateboard park project from part (a), before the reduction of time in any activity, will be repeated at another town named Campville, but with the addition of one extra activity.

     

    The new activity, `N`, will take six days to complete and has a float time of one day.

     

    Activity `N` will finish at the same time as the project.

     

     i.  Add activity `N` to the network below.   (1 mark) 


      
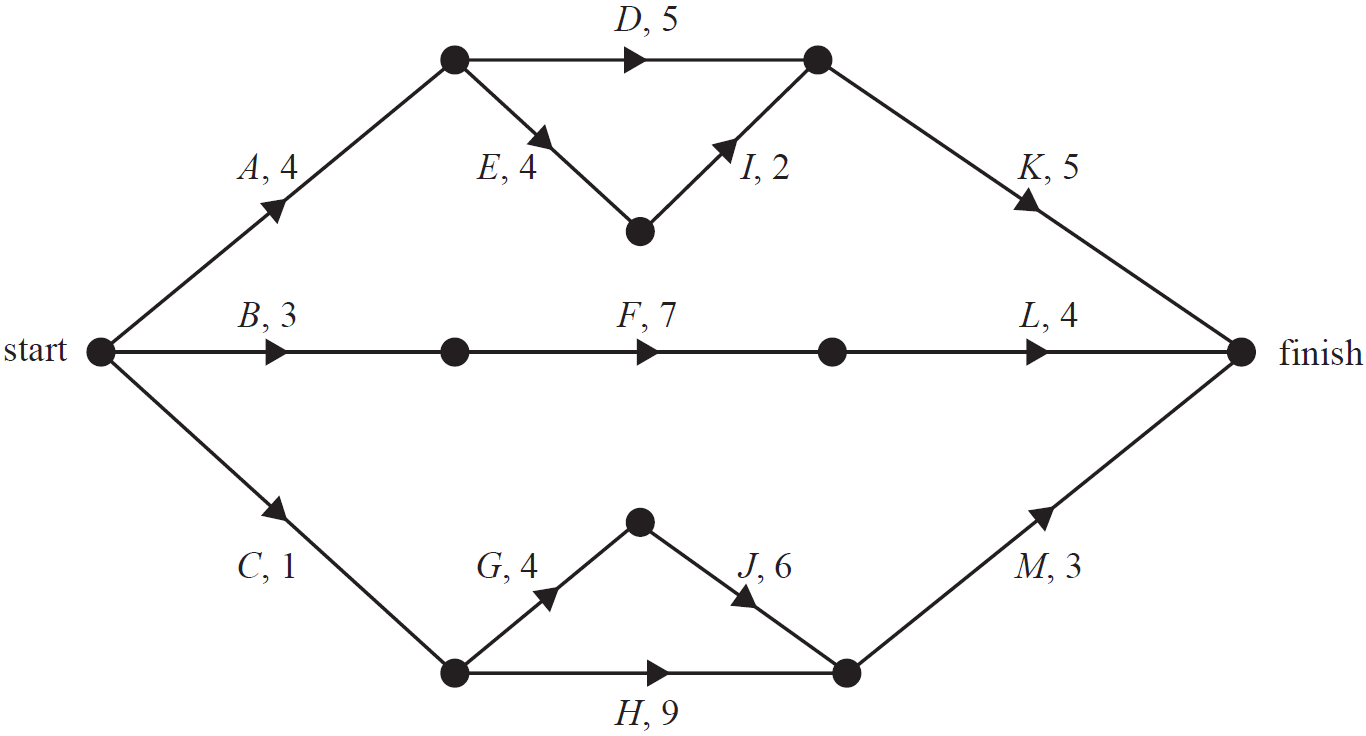
    ii.  What is the latest start time for activity `N`?   (1 mark)

Show Answers Only
  1. `11\ text(days)`
  2. `AEIK`
  3. `text(Activity)\ H`
  4. `text(Minimum cost of $2000 when activity)\ I\ text(is reduced by 1 day.)`

    2. `9\ text(days from the start)`
Show Worked Solution
a.    `text(EST)` `= 1 + 4 + 6`
    `= 11\ text(days)`

  
b.   `text(Critical Path:)\ AEIK`

♦♦ Mean mark part (c) 37%, part (d) 21%.
MARKER’S COMMENT: In part (d), `ADK` cannot be crashed, therefore shortest duration is 14 days. Activity `I` is cheapest to reduce.
  

c.   `text(Activity)\ H`
  

d.   `text(Minimum days to complete is 14 days by reducing)`

`text(either)\ E\ text(or)\ I\ text(by 1 day.)`

`:. text(Minimum cost of $2000 when activity)\ I\ text(is reduced)`

`text(by 1 day.)`
  

e.i.   

♦♦ Mean mark part (e)(i) 21%, (e)(ii) 27%.
MARKER’S COMMENT: In (e)(ii), activity `N` must have an arrow on it.
  

e.ii.    `text(LST)` `=\ text(critical path time − 6 days)`
    `= 15-6`
    `= 9\ text(days from the start.)`

NETWORKS, FUR2 2009 VCAA 4

A walkway is to be built across the lake.

Eleven activities must be completed for this building project.

The directed network below shows the activities and their completion times in weeks.
 

NETWORKS, FUR2 2009 VCAA 4
 

  1. What is the earliest start time for activity `E`?   (1 mark)

  2. Write down the critical path for this project.   (1 mark)

  3. The project supervisor correctly writes down the float time for each activity that can be delayed and makes a list of these times.

     

    Determine the longest float time, in weeks, on the supervisor’s list.   (1 mark)

A twelfth activity, `L`, with duration three weeks, is to be added without altering the critical path.

Activity `L` has an earliest start time of four weeks and a latest start time of five weeks.

 

NETWORKS, FUR2 2009 VCAA 4

  1. Draw in activity `L` on the network diagram above.   (1 mark)

  2. Activity `L` starts, but then takes four weeks longer than originally planned.

     

    Determine the total overall time, in weeks, for the completion of this building project.   (1 mark)

Show Answers Only
  1. `7`
  2. `BDFGIK`
  3. `H\ text(or)\ J\ text(can be delayed for)`
    `text(a maximum of 3 weeks.)`
  4.  
    NETWORKS, FUR2 2009 VCAA 4 Answer
  5. `text(25 weeks)`
Show Worked Solution

a.   `7\ text(weeks)`

♦ Mean mark of all parts (combined): 44%.
  

b.   `BDFGIK`
  

c.   `H\ text(or)\ J\ text(can be delayed for a maximum)`

`text(of 3 weeks.)`
  

d.    NETWORKS, FUR2 2009 VCAA 4 Answer

  
e.   `text(The new critical path is)\ BLEGIK.`

`L\ text(now takes 7 weeks.)`

`:.\ text(Time for completion)`

`= 4 + 7 + 1 + 5 + 2 + 6`

`= 25\ text(weeks)`