An upgrade to the supermarket requires the completion of 11 activities, \(A\) to \(K\). The directed network below shows these activities and their completion time, in weeks. The minimum completion time for the project is 29 weeks. --- 1 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) --- Use the following information to answer parts c-e. A change is made to the order of activities. The table below shows the activities and their new latest starting times in weeks. \begin{array}{|c|c|} A dummy activity is now required in the network. --- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) ---
\hline
\textbf{Activity} & \textbf{Latest Starting}\\
&\textbf{time} \text{(weeks)}\\
\hline A & 0 \\
\hline B & 2 \\
\hline C & 10 \\
\hline D & 9 \\
\hline E & 13 \\
\hline F & 14 \\
\hline G & 18 \\
\hline H & 17 \\
\hline I & 19 \\
\hline J & 25 \\
\hline K & 22 \\
\hline
\end{array}
Networks, GEN1 2022 VCAA 7-8 MC
A project involves 11 activities, \(A\) to \(K\).
The table below shows the earliest start time and duration, in days, for each activity.
The immediate predecessor(s) of each activity is also shown.
\begin{array} {|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ \textbf{Activity}\ \ & \textbf{Earliest} & \ \ \textbf{Duration}\ \ & \textbf{Immediate}\\
& \textbf{start time} \rule[-1ex]{0pt}{0pt} & &\textbf{predecessor}\\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & \text{0} & \text{6} & \text{-}\\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & \text{0} & \text{7} & \text{-}\\
\hline
\rule{0pt}{2.5ex} C \rule[-1ex]{0pt}{0pt} & \text{6} & \text{10} & A\\
\hline
\rule{0pt}{2.5ex} D \rule[-1ex]{0pt}{0pt} & \text{6} & \text{7} & A\\
\hline
\rule{0pt}{2.5ex} E \rule[-1ex]{0pt}{0pt} & \text{7} & \text{8} & B\\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & \text{15} & \text{2} & D,\ E\\
\hline
\rule{0pt}{2.5ex} G \rule[-1ex]{0pt}{0pt} & \text{15} & \text{2} & E\\
\hline
\rule{0pt}{2.5ex} H \rule[-1ex]{0pt}{0pt} & \text{17} & \text{3} & G\\
\hline
\rule{0pt}{2.5ex} I \rule[-1ex]{0pt}{0pt} & \text{20} & \text{6} & C,\ F,\ H\\
\hline
\rule{0pt}{2.5ex} J \rule[-1ex]{0pt}{0pt} & \text{17} & \text{5} & G\\
\hline
\rule{0pt}{2.5ex} K \rule[-1ex]{0pt}{0pt} & \text{26} & \text{2} & I,\ J\\
\hline
\end{array}
Question 7
A directed network for this project will require a dummy activity.
The dummy activity will be drawn from the end of
- activity \(A\) to the start of activity \(D\).
- activity \(E\) to the start of activity \(F\).
- activity \(F\) to the start of activity \(I\).
- activity \(G\) to the start of activity \(H\).
- activity \(I\) to the start of activity \(J\).
Question 8
When this project is completed in the minimum time, the sum of all the float times, in days, will be
- 0
- 16
- 18
- 20
- 28
Networks, GEN1 2023 VCAA 38 MC
A particular building project has ten activities that must be completed.
These activities and their immediate predecessor(s) are shown in the table below.
\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Activity} \rule[-1ex]{0pt}{0pt} & \textbf{Immediate predecessor(s)} \\
\hline
A & - \\
\hline
B & - \\
\hline
C & A \\
\hline
D & A \\
\hline
E & B \\
\hline
F & D, E \\
\hline
G & C, F \\
\hline
H & F \\
\hline
I & D, E \\
\hline
J & H, I \\
\hline
\end{array}
A directed graph that could represent this project is
NETWORKS, FUR2 2020 VCAA 5
The Sunny Coast cricket clubroom is undergoing a major works project.
This project involves nine activities: `A` to `I`.
The table below shows the earliest start time (EST) and duration, in months, for each activity.
The immediate predecessor(s) is also shown.
The duration for activity `C` is missing.
The information in the table above can be used to complete a directed network.
This network will require a dummy activity.
- Complete the following sentence by filling in the boxes provided. (1 mark)
This dummy activity could be drawn as a directed edge from the end of activity to the start of activity--- 0 WORK AREA LINES (style=lined) ---
- What is the duration, in months, of activity `C`? (1 mark)
--- 5 WORK AREA LINES (style=blank) ---
--- 2 WORK AREA LINES (style=lined) ---
- Name the four activities that have a float time. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- The project is to be crashed by reducing the completion time of one activity only.
What is the minimum time, in months, that the project can be completed in? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
NETWORKS, FUR1 2019 VCAA 7 MC
A project involves nine activities, `A` to `I`.
The immediate predecessor(s) of each activity is shown in the table below.
| Activity | Immediate predecessor(s) |
|
| `A` | `-` | |
| `B` | `A` | |
| `C` | `A` | |
| `D` | `B` | |
| `E` | `B, C` | |
| `F` | `D` | |
| `G` | `D` | |
| `H` | `E, F` | |
| `I` | `G, H` |
A directed network for this project will require a dummy activity.
The dummy activity will be drawn from the end of
- activity `B` to the start of activity `C`.
- activity `B` to the start of activity `E`.
- activity `D` to the start of activity `E`.
- activity `E` to the start of activity `H`.
- activity `E` to the start of activity `F`.
NETWORKS, FUR1 2010 VCAA 8 MC
A project has 12 activities. The network below gives the time (in hours) that it takes to complete each activity.
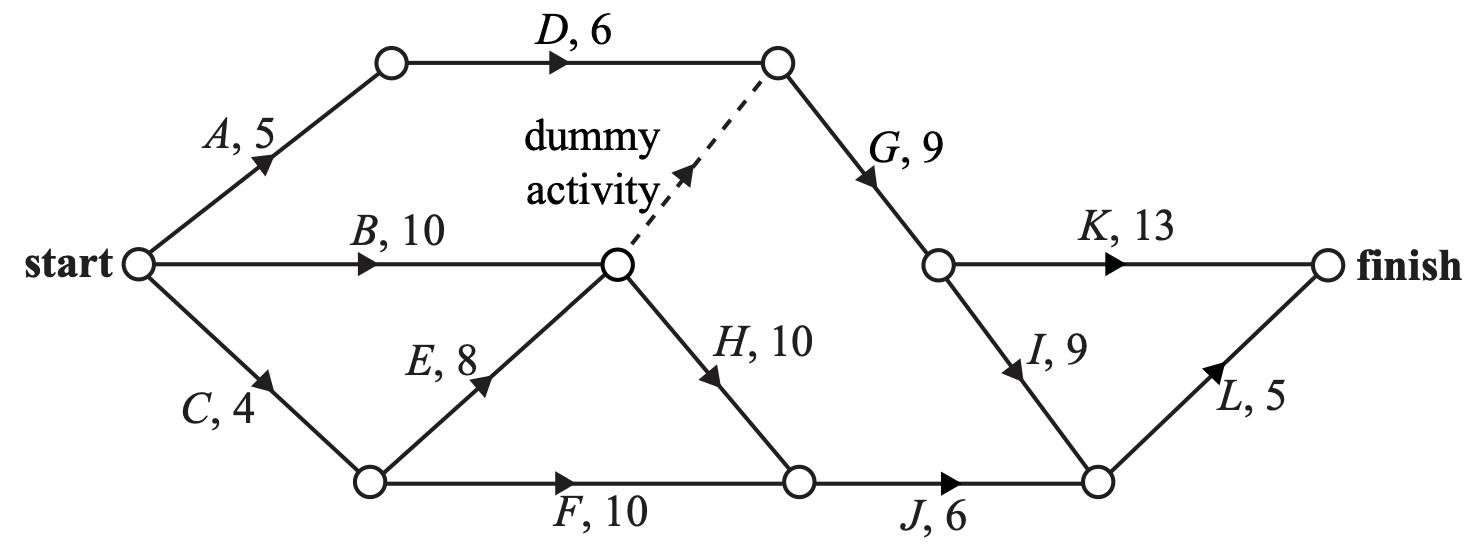
The critical path for this project is
A. `ADGK`
B. `ADGIL`
C. `BHJL`
D. `CEGIL`
E. `CEHJL`
NETWORKS, FUR1 2006 VCAA 9 MC
The network below shows the activities and their completion times (in hours) that are needed to complete a project.
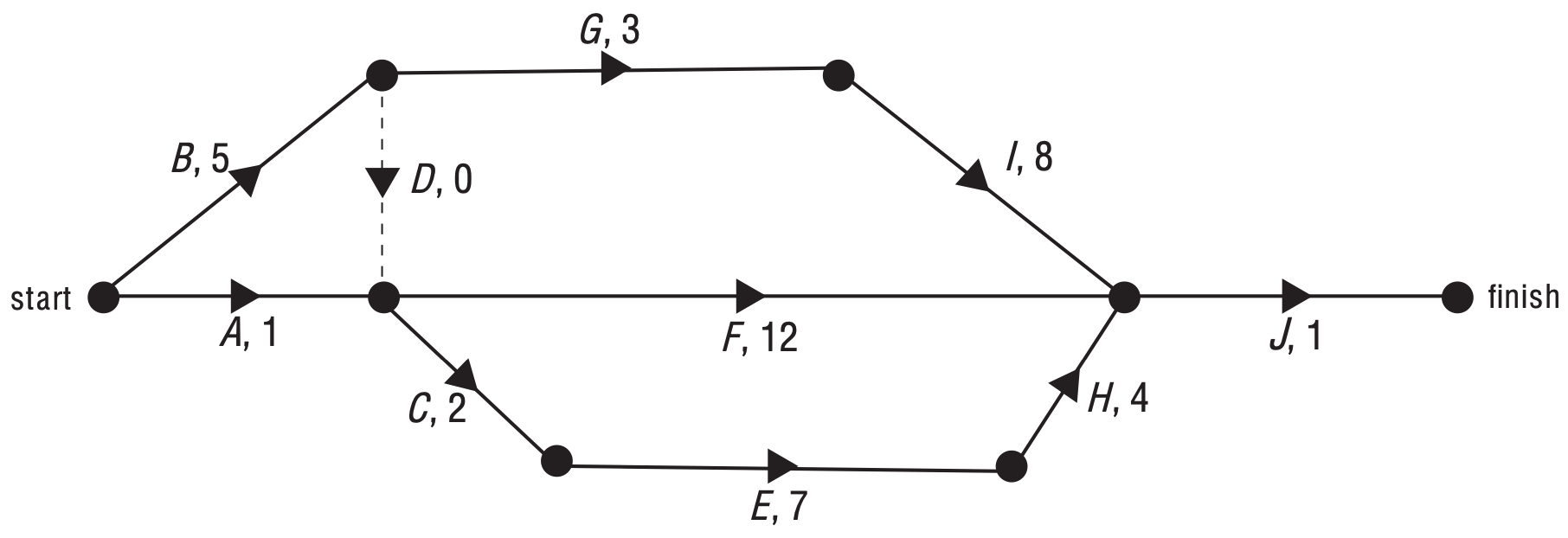
The project is to be crashed by reducing the completion time of one activity only.
This will reduce the completion time of the project by a maximum of
A. 1 hour
B. 2 hours
C. 3 hours
D. 4 hours
E. 5 hours
NETWORKS, FUR1 2007 VCAA 5-6 MC
The following network shows the activities that are needed to complete a project and their completion times (in hours).
Part 1
Which one of the following statements regarding this project is false?
A. Activities `A, B` and `C` all have the same earliest start time.
B. There is only one critical path for this project.
C. Activity `J` may start later than activity `H.`
D. The shortest path gives the minimum time for project completion.
E. Activity `L` must be on the critical path.
Part 2
The earliest start time for activity `L`, in hours, is
A. 11
B. 12
C. 14
D. 15
E. 16
NETWORKS, FUR1 2011 VCAA 8 MC
NETWORKS, FUR2 2015 VCAA 3
Nine activities are needed to prepare a daily delivery of groceries from the factory to the towns.
The duration, in minutes, earliest starting time (EST) and immediate predecessors for these activities are shown in the table below.
The directed network that shows these activities is shown below.
All nine of these activities can be completed in a minimum time of 26 minutes.
- What is the EST of activity `D`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- What is the latest starting time (LST) of activity `D`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Given that the EST of activity `I` is 22 minutes, what is the duration of activity `H`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Write down, in order, the activities on the critical path. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Activities `C` and `D` can only be completed by either Cassie or Donna.
One Monday, Donna is sick and both activities `C` and `D` must be completed by Cassie. Cassie must complete one of these activities before starting the other.
What is the least effect of this on the usual minimum preparation time for the delivery of groceries from the factory to the five towns? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Every Friday, a special delivery to the five towns includes fresh seafood. This causes a slight change to activity `G`, which then cannot start until activity `F` has been completed.
i. Michael was the best player in 2014 and he considered purchasing cricket equipment that was valued at $750.
On the directed graph below, show this change without duplicating any activity? (1 mark)
- ii. What effect does the inclusion of seafood on Fridays have on the usual minimum preparation time for deliveries from the factory to the five towns? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
NETWORKS, FUR2 2012 VCAA 2
Thirteen activities must be completed before the produce grown on a farm can be harvested.
The directed network below shows these activities and their completion times in days.
- Determine the earliest starting time, in days, for activity `E`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- A dummy activity starts at the end of activity `B`.
Explain why this dummy activity is used on the network diagram. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Determine the earliest starting time, in days, for activity `H`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- In order, list the activities on the critical path. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Determine the latest starting time, in days, for activity `J`. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---





