SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

NETWORKS, FUR1 2021 VCAA 8 MC

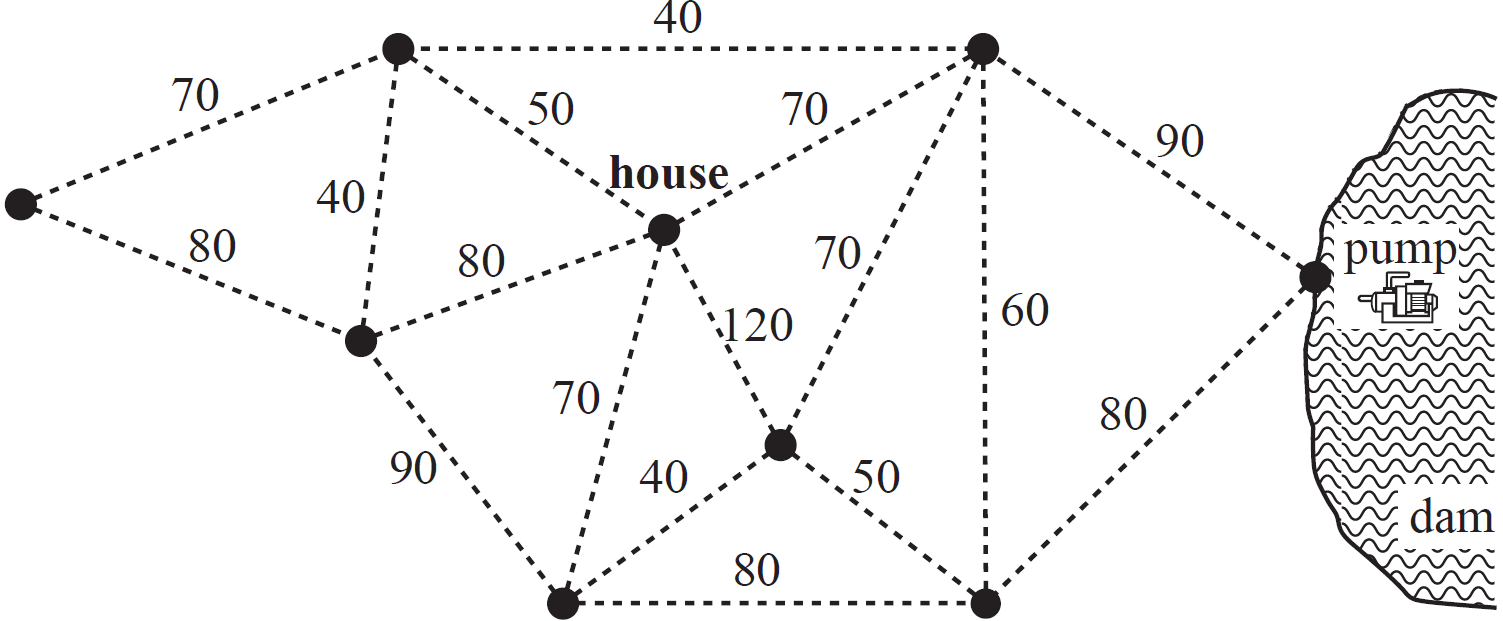
A network of roads connecting towns in an alpine region is shown below.

The distances between neighbouring towns, represented by vertices, are given in kilometres.
 

The region receives a large snowfall, leaving all roads between the towns closed to traffic.

To ensure each town is accessible by car from every other town, some roads will be cleared.

The minimal total length of road, in kilometres, that needs to be cleared is

  1. 361 if  `x` = 50 and  `y` = 55
  2. 361 if  `x` = 50 and  `y` = 60
  3. 366 if  `x` = 55 and  `y` = 55
  4. 366 if  `x` = 55 and  `y` = 60
  5. 371 if  `x` = 55 and  `y` = 65
Show Answers Only

`B`

Show Worked Solution

`text{A partial minimal spanning tree can be drawn:}`
 

`text{Consider each option:}`

♦ Mean mark 48%.

`A:\ text{If} \ x=50 \ text{(include),} \ y = 55 \ text{(include)}`

   `-> \ text{Total length} = 251 + 50 + 55 != 361 \ text{(incorrect)}`

`B:\ text{If} \ x=50 \ text{(include),} \ y = 60 \ text{(include)}`

   `-> \ text{Total length} = 251 + 50 + 55 = 356 \ text{(correct)}`

`text{Similarly, options} \ C, D, E \ text{can be shown to be incorrect.}`

`=> B`

NETWORKS, FUR1 2020 VCAA 5 MC

The network below shows the distances, in metres, between camp sites at a camping ground that has electricity.

The vertices `A` to `I` represent the camp sites.
 


 

The minimum length of cable required to connect all the camp sites is 53 m.

The value of `x`, in metres, is at least

  1.  5
  2.  6
  3.  8
  4.  9
  5. 11
Show Answers Only

`D`

Show Worked Solution

`text(One strategy – Using Prim’s Algorith)`

`text(Starting at)\ A`

`text(1st edge) : AH = 6`

`text(2nd edge) : HG = 5`

`text(then …)\ AB = 7,\ GI = 9,\ IE = 6,\ EF = 5`

`DE = 8,\ CD = 7`
 

`text {Total length = 53 m (not including}\ x text{)}`

`text(If)\ \ x < 9, x\ text(would replace)\ GI\ text(and minimum`

`text(length would be less than 53m.)`

`=>  D`

NETWORKS, FUR1-NHT 2019 VCAA 5 MC

In the graph below, the vertices represent electricity transformer substations.

The numbers on the edges of the graph show the length, in kilometres, of cables that connect these substations.
  

 
 

What is the minimum length of cable, in kilometres, that is necessary to make sure that each substation remains connected to the network?

  1. 65
  2. 71
  3. 73
  4. 74
  5. 77
Show Answers Only

`B`

Show Worked Solution

`text(Minimum length)` `= 7 + 8 + 10 + 7 + 9 + 8 + 11 + 11`
  `= 71\ text(km)`

`=>  B`

NETWORKS, FUR1 2019 VCAA 5 MC

The following diagram shows the distances, in metres, along a series of cables connecting a main server to seven points, `A` to `G`, in a computer network.
 


 

The minimum length of cable, in metres, required to ensure that each of the seven points is connected to the main server directly or via another point is

  1. 175
  2. 203
  3. 208
  4. 221
  5. 236
Show Answers Only

`B`

Show Worked Solution

`text(Using Prim’s Algorithm:)`

`text{Edge 1: main server to D (15)}`

`text{Edge 2: DE (28)}`

`text{Edge 3: EG (30)}`

`text{Edge 4: GF (32)}`

`text{Edge 5: EA (35)}`

`text{Edge 6: AB (28)}`

`text{Edge 7: GC (35)}`
 

`:.\ text(Minimum length)`

`= 15 + 28 + 30 + 32 + 35 + 28 + 35`

`= 203\ text(m)`

`=>  B`

NETWORKS, FUR2 2017 VCAA 3

While on holiday, four friends visit a theme park where there are nine rides.

On the graph below, the positions of the rides are indicated by the vertices.

The numbers on the edges represent the distances, in metres, between rides.
 

  1. Electrical cables are required to power the rides.
    These cables will form a connected graph.
    The shortest total length of cable will be used.

    1. Give a mathematical term to describe a graph that represents these cables.  (1 mark)
    2. Draw in the graph that represents these cables on the diagram below.  (1 mark)
       
Show Answers Only

a.i.   `text{Minimum spanning tree (shortest length required).}`

 

a.ii.   
Show Worked Solution

a.i.   `text{Minimal spanning tree (shortest length required).}`

 

a.ii.   

NETWORKS, FUR2 2008 VCAA 1

James, Dante, Tahlia and Chanel are four children playing a game.

In this children’s game, seven posts are placed in the ground.

The network below shows distances, in metres, between the seven posts.

The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.

This will be a minimal spanning tree.

 

NETWORKS, FUR2 2008 VCAA 11
 

  1. Draw in a minimal spanning tree for this network on the diagram below.  (1 mark)


NETWORKS, FUR2 2008 VCAA 12

  1. Determine the length, in metres, of this minimal spanning tree.  (1 mark)
  2. How many different minimal spanning trees can be drawn for this network?  (1 mark)

 

Show Answers Only
  1.  
    networks-fur2-2008-vcaa-1-answer1
    `text(or)`
    networks-fur2-2008-vcaa-1-answer2
  2. `16\ text(metres)`
  3. `2`
Show Worked Solution
a.    networks-fur2-2008-vcaa-1-answer1

`text(or)`

networks-fur2-2008-vcaa-1-answer2

 

b.   `text(Length of minimal spanning tree)`

`= 4 + 2 + 2 + 3 + 2 + 3`

`= 16\ text(metres)`
 

c.   `2`

NETWORKS, FUR2 2011 VCAA 2

At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
 

NETWORKS, FUR2 2011 VCAA 2 
 

All locations are to be connected using the smallest total length of water pipe possible.

  1. On the diagram, show where these water pipes will be placed.  (1 mark)
  2. Calculate the total length, in metres, of water pipe that is required.  ( 1 mark) 
Show Answers Only
  1.  
    NETWORKS, FUR2 2011 VCAA 2 Answer
  2. `510\ text(metres)`
Show Worked Solution
a.    NETWORKS, FUR2 2011 VCAA 2 Answer

 

b.   `text(Total length of water pipe)`

`= 60 + 60 + 40 + 60 + 50 + 40 + 60`

`+ 40 + 50 + 50`

`= 510\ text(metres)`

NETWORKS, FUR2 2012 VCAA 1

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
 

NETWORKS, FUR2 2012 VCAA 1
 

    1. Determine the shortest distance between the house and the pump.  (1 mark)
    2. How many vertices on the network diagram have an odd degree?  (1 mark)
    3. The total length of all edges in the network is 1180 metres.

       

      A journey starts and finishes at the house and travels along every edge in the network.

       

      Determine the shortest distance travelled.  (1 mark)

The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

This minimum length of pipe is laid along some of the edges in the network.

    1. On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm.  (1 mark)

       

         
        NETWORKS, FUR2 2012 VCAA 1
       

    2. What is the mathematical term that is used to describe this minimum length of pipe in part i.?  (1 mark)
Show Answers Only
    1. `160\ text(m)`
    2. `2`
    3. `1250\ text(m)`
    1.  
      NETWORKS, FUR2 2012 VCAA 1 Answer
    2. `text(Minimal spanning tree)`
Show Worked Solution

a.i.   `text(Shortest distance)`

`=70 + 90`

`= 160\ text(m)`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (a)(ii).

 

a.ii.   `2\ text{(the house and the top right vertex)}`

 

a.iii.   `text{An Eulerian path is possible if it starts at}`

♦♦ “Very poorly answered”.
MARKER’S COMMENT: An Euler circuit is optimal but not possible here because of the two odd degree vertices.

   `text{the house (odd vertex) and ends at the top}`

   `text{right vertex (the other odd vertex). However,}`

   `text{70 metres must be added to return to the}`

   `text{house.}`

`:.\ text(Total distance)` `= 1180 + 70`
  `= 1250\ text(m)`

 

b.i.    NETWORKS, FUR2 2012 VCAA 1 Answer

 

b.ii.   `text(Minimal spanning tree)`