SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Matrices, GEN1 2024 VCAA 37 MC

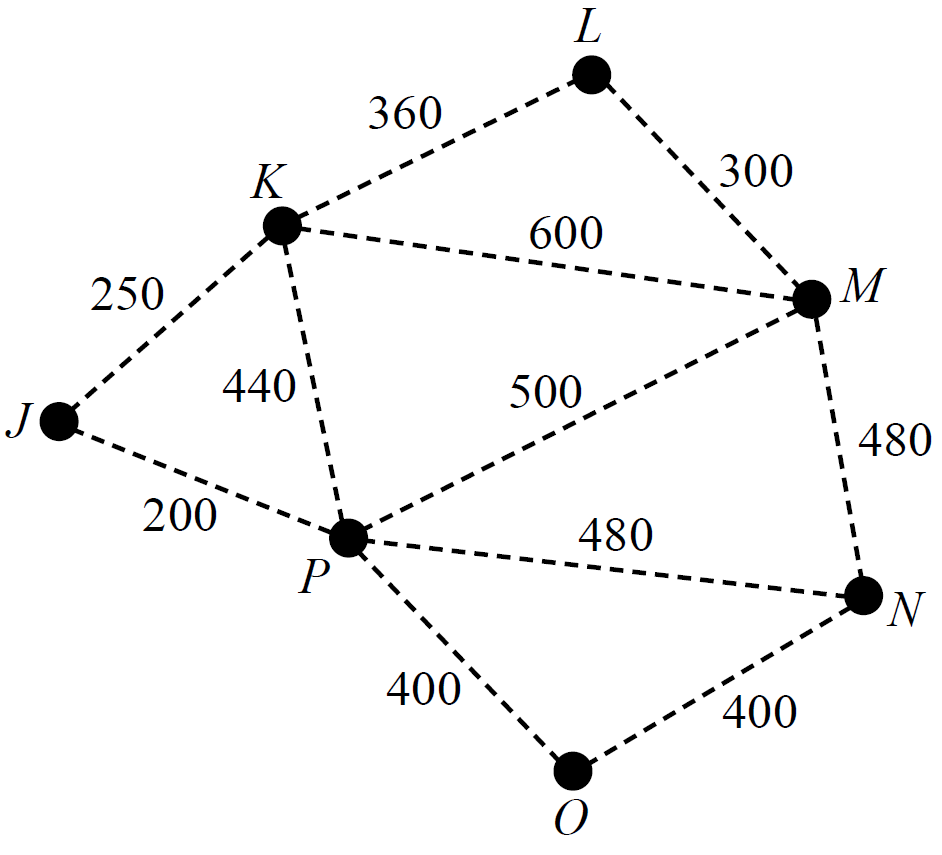
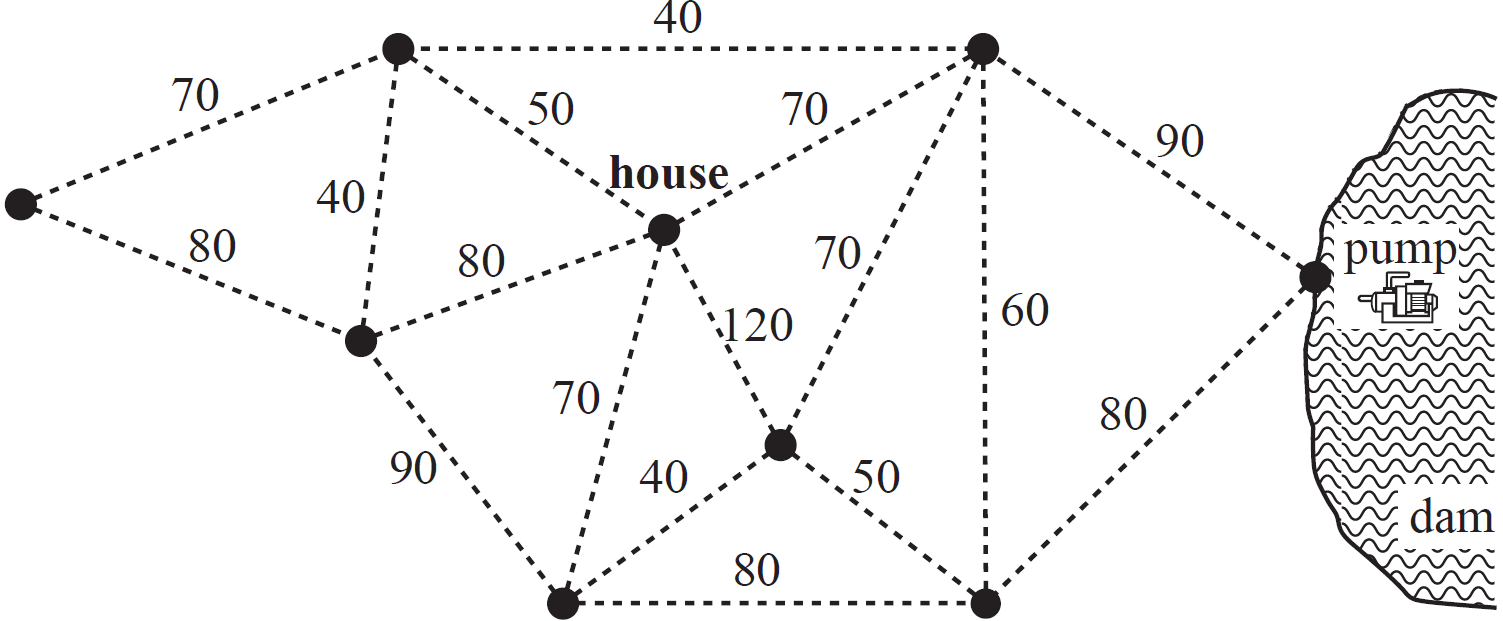
The network below represents paths through a park from the carpark to a lookout.

The vertices represent various attractions, and the numbers on the edges represent the distances between them in metres.
 

The shortest path from the carpark to the lookout is 34 m .

This can be achieved when

  1. \(x=8\)  and  \(y=8\)
  2. \(x=9\)  and  \(y=7\)
  3. \(x=10\)  and  \(y=6\)
  4. \(x=11\)  and  \(y=5\)
Show Answers Only

\(D\)

Show Worked Solution

\(\text{By trial and error}\)

\(\text{Consider Option D:}\ \ \ x=11, y=5\)

\(\text{Shortest path}\ = 10+11+8+5=34\ \checkmark\)
  

 
\(\Rightarrow D\)


♦ Mean mark 40%

NETWORKS, FUR2 2021 VCAA 2

George lives in Town `G` and Maggie lives in Town `M`.

The diagram below shows the network of main roads between Town `G` and Town `M`.

The vertices `G, H, I, J, K, L, M, N` and `O` represent towns.

The edges represent the main roads. The number on the edges indicate the distance, in kilometres, between adjacent towns.
 

  1. What is the shortest distance, in kilometres, between Town `G` and Town `M`?   (1 mark)

  2. George plans to travel to Maggie's house. He will pass through all the towns shown above.
  3. George plans to take the shortest route possible.
  4. Which town will George pass through twice?    (1 mark)

Show Answers Only
  1. `86 \ text{km}`
  2. `text{Passes through town} \ K \ text{twice.}`
Show Worked Solution
a.  `text{Shortest route}` `= G \ O \ N \ M`
    `= 28 + 42 + 16`
    `= 86 \ text{km}`

 
b.  `text{Shortest route through all towns} = G \ H \ I \ K \ L \ K \ J\ O \ N \ M`

`:. \ text{Passes through town} \ K \ text{twice}`

NETWORKS, FUR2 2020 VCAA 3

A local fitness park has 10 exercise stations: `M` to `V`.

The edges on the graph below represent the tracks between the exercise stations.

The number on each edge represents the length, in kilometres, of each track.
 


 

The Sunny Coast cricket coach designs three different training programs, all starting at exercise station `S`.

  Training program 
number		 Training details
  1 The team must run to exercise station `O`.
  2 The team must run along all tracks just once.
  3 The team must visit each exercise station and return to  exercise station `S`.

 

  1. What is the shortest distance, in kilometres, covered in training program 1?  (1 mark)

  2.  i. What mathematical term is used to describe training program 2?   (1 mark)

  3. ii. At which exercise station would training program 2 finish?  (1 mark)

  4. To complete training program 3 in the minimum distance, one track will need to be repeated.

     

    Complete the following sentence by filling in the boxes provided.  (1 mark)


    This track is between exercise station   
     
    		 and exercise station   
     
Show Answers Only
  1. `3.2\ text(km)`
  2.  i. `text(Eulerian trail)`
  3. ii. `text(Station)\ P`
  4. `S and T`
Show Worked Solution
a.   `text(Shortest distance)` `= STUVO`
    `= 0.6 + 1.2 + 0.6 + 0.8`
    `= 3.2\ text(km)`

 

b.i.  `text(Eulerian trail)`
 

b.ii.  `text(Station)\ P\ text{(only other vertex with}\ S\ text{to have odd degree)} `

♦♦ Mean mark part (c) 25%.

 

c.   `S and T`

NETWORKS, FUR2-NHT 2019 VCAA 1

A zoo has an entrance, a cafe and nine animal exhibits: bears `(B)`, elephants `(E)`, giraffes `(G)`, lions `(L)`, monkeys `(M)`, penguins `(P)`, seals `(S)`, tigers `(T)` and zebras `(Z)`.

The edges on the graph below represent the paths between the entrance, the cafe and the animal exhibits. The numbers on each edge represent the length, in metres, along that path. Visitors to the zoo can use only these paths to travel around the zoo.
  

 
 

  1. What is the shortest distance, in metres, between the entrance and the seal exhibit `(S)`?   (1 mark)

  2. Freddy is a visitor to the zoo. He wishes to visit the cafe and each animal exhibit just once, starting and ending at the entrance.
  3. i. What is the mathematical term used to describe this route?   (1 mark)

  4. ii. Draw one possible route that Freddy may take on the graph below.   (1 mark)


 

A reptile exhibit `(R)` will be added to the zoo.

A new path of length 20 m will be built between the reptile exhibit `(R)` and the giraffe exhibit `(G)`.

A second new path, of length 35 m, will be built between the reptile exhibit `(R)` and the cafe.

  1. Complete the graph below with the new reptile exhibit and the two new paths added. Label the new vertex `R` and write the distances on the new edges.   (1 mark)

     


 

  1. The new paths reduce the minimum distance that visitors have to walk between the giraffe exhibit `(G)` and the cafe.

     

    By how many metres will these new paths reduce the minimum distance between the giraffe exhibit `(G)` and the cafe?   (1 mark)

Show Answers Only
  1.  `45\ text(metres)`
  2. i.  `text(Hamilton cycle.)`
    ii. `text(See Worked Solutions)`
  3.  `text(See Worked Solutions)`
  4.  `85\ text(metres)`
Show Worked Solution

a.   `45\ text(metres)`
 

b.i.   `text(Hamilton cycle.)`
 

b.ii.  

`text(Possible route:)`

`text(entrance)\ – LGTMCEBSZP\ –\ text(entrance)`

 

c.  

 

d.  `text{Minimum distance (before new exhibit)}`

`= GLTMC`

`= 15 + 35 + 40 + 50`

`= 140\ text(m)`
 

`:.\ text(Reduction in minimum distance)`

`= 140 – (20 + 35)`

`= 85\ text(m)`

NETWORKS, FUR1 2018 VCAA 2 MC

Niko drives from his home to university.

The network below shows the distances, in kilometres, along a series of streets connecting Niko’s home to the university.

The vertices `A`, `B`, `C`, `D` and `E` represent the intersection of these streets.
 


 

The shortest path for Niko from his home to the university could be found using

  1. a minimum cut.
  2. Prim’s algorithm.
  3. Dijkstra’s algorithm.
  4. critical path analysis.
  5. the Hungarian algorithm.
Show Answers Only

`C`

Show Worked Solution

`text(Djikstra’s algorithm can be used to find the)`

`text(shortest path.)`

`text(Note that Prim’s algorithm can be used to)`

`text(find the minimum spanning tree but doesn’t)`

`text(necessary provide the shortest path from 2)`

`text(nominated vertices.)`

`=> C`

NETWORKS, FUR1 2007 VCAA 4 MC

The following network shows the distances, in kilometres, along a series of roads that connect town `A` to town `B.`
 

 

 
The shortest distance, in kilometres, to travel from town `A` to town `B` is

A.     `9`

B.   `10`

C.   `11`

D.   `12`

E.   `13`

Show Answers Only

`B`

Show Worked Solution

`text(Shortest path)`

`= 4 + 1 + 3 + 2`

`= 10`

`=>  B`

NETWORKS, FUR1 2014 VCAA 3 MC

The diagram below shows the network of roads that Stephanie can use to travel between home and school.
 

 
The numbers on the roads show the time, in minutes, that it takes her to ride a bicycle along each road.

Using this network of roads, the shortest time that it will take Stephanie to ride her bicycle from home to school is 

A.  `12\ text(minutes)`

B.  `13\ text(minutes)`

C.  `14\ text(minutes)`

D.  `15\ text(minutes)`

E.  `16\ text(minutes)`

Show Answers Only

`C`

Show Worked Solution

`text(Shortest time riding)`

`=3+2+3+4+2`

`=14\ text(minutes)`

`=> C`

NETWORKS, FUR2 2011 VCAA 1

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.

 

  1. In kilometres, what is the shortest distance between Farnham and Carrie?   (1 mark)

  2. How many different ways are there to travel from Farnham to Carrie without passing through any town more than once?   (1 mark)

An engineer plans to inspect all of the roads in this network.

He will start at Dunlop and inspect each road only once.

  1. At which town will the inspection finish?   (1 mark)

Another engineer decides to start and finish her road inspection at Dunlop.

If an assistant inspects two of the roads, this engineer can inspect the remaining six roads and visit each of the other five towns only once.

  1. How many kilometres of road will the assistant need to inspect?   (1 mark)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
  3. `text(Bredon)`
  4. `240\ text(km)`
Show Worked Solution

a.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`
  

b.   `text(Different paths are)`

`FDC, FEDC, FEBC,`

`FEABC, FDEBC,`

`FDEABC`

`:. 6\ text(different ways)`
  

c.   `text(A possible path is)\ DFEABCDEB\ text(and will finish)`

`text{at Bredon (the other odd-degree vertex).}`
  

d.   `text(If the engineer’s path is)`

`DFEABCD,`

`text(Distance assistant inspects)`

`= 110 + 130`

`= 240\ text(km)`

NETWORKS, FUR2 2015 VCAA 2

The factory supplies groceries to stores in five towns, `Q`, `R`, `S`, `T` and `U`, represented by vertices on the graph below.
 

Networks, FUR2 2015 VCAA 2
 

The edges of the graph represent roads that connect the towns and the factory.

The numbers on the edges indicate the distance, in kilometres, along the roads.

Vehicles may only travel along the road between towns `S` and `Q` in the direction of the arrow due to temporary roadworks.

Each day, a van must deliver groceries from the factory to the five towns.

The first delivery must be to town `T`, after which the van will continue on to the other four towns before returning to the factory.

  1. i. The shortest possible circuit from the factory for this delivery run, starting from town `T`, is not Hamiltonian.
     
    Complete the order in which these deliveries would follow this shortest possible circuit.   (1 mark)

     factory – `T` – ___________________________ – factory

  2. ii. With reference to the town names in your answer to part (a)(i), explain why this shortest circuit is not a Hamiltonian circuit.   (1 mark)

  3. Determine the length, in kilometres, of a delivery run that follows a Hamiltonian circuit from the factory to these stores if the first delivery is to town `T`.   (1 mark)

Show Answers Only

a.i.  `text(factory)\-T-S-Q-R-S-U-text(factory)`

aii.  `text(The van passes through town)\ S\ text(twice.)`

b.   `162\ text(km)`

Show Worked Solution

a.i.   `text(factory)\-T-S-Q-R-S-U- text(factory)`
  

a.ii.   `text(The van passes through town)\ S\ text(twice.)`
  

b.   `text(Hamiltonian circuit is)`

`text(factory)\-T-S-R-Q-U-text(factory)`

`= 44 + 38 + 12 + 8 + 38 + 22`

`= 162\ text(km)`

NETWORKS, FUR2 2015 VCAA 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
 

Networks, FUR2 2015 VCAA 11

 
The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

  1. What is the cost, in dollars, of installing the cable between server `L` and server `M`?   (1 mark)

  2. What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`?   (1 mark)

  3. An inspector checks the cables by walking along the length of each cable in one continuous path.
    To avoid walking along any of the cables more than once, at which vertex should the inspector start and where would the inspector finish?   (1 mark)

     

  4. The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.
    i.     The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

    Draw the minimum spanning tree on the plan below?   (1 mark)


    Networks, FUR2 2015 VCAA 12
  5. ii. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven. 

    How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?
    A copy of the graph above is provided below to assist with your working.   (1 mark)

    Networks, FUR2 2015 VCAA 12

Show Answers Only
  1. `$300`
  2. `$920`
  3. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
  4. i. 

 Networks, FUR2 2015 VCAA 12 Answer
d.ii.`$120`

Show Worked Solution

a.   `$300`
  

b.   `text(C)text(ost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`
  

c.   `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.
d.i.    Networks, FUR2 2015 VCAA 12 Answer

 

d.ii.   `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)` `= 600 – 480`
  `= $120`

NETWORKS, FUR2 2012 VCAA 1

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
 

NETWORKS, FUR2 2012 VCAA 1
 

    1. Determine the shortest distance between the house and the pump.   (1 mark)

    2. How many vertices on the network diagram have an odd degree?   (1 mark)
    3. The total length of all edges in the network is 1180 metres.
    4. A journey starts and finishes at the house and travels along every edge in the network.
    5. Determine the shortest distance travelled.   (1 mark)

The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

This minimum length of pipe is laid along some of the edges in the network.

    1. On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm.   (1 mark)

       

     NETWORKS, FUR2 2012 VCAA 1

    1. What is the mathematical term that is used to describe this minimum length of pipe in part i.?   (1 mark)

Show Answers Only

  1. i.  `160\ text(m)`
    ii.  `2`
    iii. `1250\ text(m)`
  2. i.
    NETWORKS, FUR2 2012 VCAA 1 Answer
    ii.     `text(Minimal spanning tree)`

Show Worked Solution

a.i.   `text(Shortest distance)`

`=70 + 90`

`= 160\ text(m)`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (a)(ii).

  

a.ii.   `2\ text{(the house and the top right vertex)}`
 

a.iii.   `text{An Eulerian path is possible if it starts at}`

♦♦ “Very poorly answered”.
MARKER’S COMMENT: An Euler circuit is optimal but not possible here because of the two odd degree vertices.

   `text{the house (odd vertex) and ends at the top}`

   `text{right vertex (the other odd vertex). However,}`

   `text{70 metres must be added to return to the}`

   `text{house.}`

`:.\ text(Total distance)` `= 1180 + 70`
  `= 1250\ text(m)`

 

b.i.    NETWORKS, FUR2 2012 VCAA 1 Answer

 

b.ii.   `text(Minimal spanning tree)`