SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, MET1 2024 VCAA 8

Let  \(g: R \rightarrow R, \ g(x)=\sqrt[3]{x-k}+m\),  where  \(k \in R \backslash\{0\}\)  and  \(m \in R\).

Let the point \(P\) be the \(y\)-intercept of the graph of  \(y=g(x)\).

  1. Find the coordinates of \(P\), in terms of \(k\) and \(m\).   (1 mark)

  2. Find the gradient of \(g\) at \(P\), in terms of \(k\).   (2 marks)

  3. Given that the graph of  \(y=g(x)\)  passes through the origin, express \(k\) in terms of \(m\).   (1 mark)

  4. Let the point \(Q\) be a point different from the point \(P\), such that the gradient of \(g\) at points \(P\) and \(Q\) are equal.
  5. Given that the graph of  \(y=g(x)\)  passes through the origin, find the coordinates of \(Q\) in terms of \(m\).   (3 marks)

Show Answers Only

a.    \(\bigg(0, -\sqrt[3]{k}+m\bigg)\)

b.    \(\dfrac{1}{3}(-k)^{-\frac{2}{3}}\)

c.    \(k=m^3\)

d.    \(Q(2m^3,2m)\)

Show Worked Solution

a.   \(g(0)=\sqrt[3]{0-k}+m=-\sqrt[3]{k}+m\)

\(P(0, -\sqrt[3]{k}+m)\)
 

b.   \(g(x)=\sqrt[3]{x-k}+m=(x-k)^{\frac{1}{3}}+m\)

  \(g^{\prime}(x)\) \(=\dfrac{1}{3}(x-k)^{-\frac{2}{3}}\)
  \(g^{\prime}(0)\) \(=\dfrac{1}{3}(0-k)^{-\frac{2}{3}}=\dfrac{1}{3}(-k)^{-\frac{2}{3}} =\dfrac{1}{3}(k)^{-\frac{2}{3}}\)
♦ Mean mark (b) 39%.
c.     \(\text{When }y=0:\)
     \(-\sqrt[3]{k}+m\) \(=0\)  
  \(\sqrt[3]{k}\) \(=m\)  
  \(k\) \(=m^3\)  
♦ Mean mark (c) 47%.
d.     \(g^{\prime}(x)\) \(=g^{\prime}(0)\)
  \(\dfrac{1}{3}(x-k)^{-\frac{2}{3}}\) \(=\dfrac{1}{3(-k)^{\frac{2}{3}}}\)
  \(\dfrac{1}{(x-k)^{\frac{2}{3}}}\) \(=\dfrac{1}{k^{\frac{2}{3}}}\)
  \((x-k)^{\frac{2}{3}}\) \(=k^{\frac{2}{3}}\)
  \((x-k)^2\) \(=k^2\)
  \(x-k\) \(=\pm k\)
  \(x\) \(=0, \ 2k\)
♦♦♦ Mean mark (d) 15%.

\(\text{When }x=2k:\)

\(y=(2k-k)^{\frac{1}{3}}+m=k^{\frac{1}{3}}+m=2m\ \text{(from (c))}\)

\(\therefore\ \text{Coordinates of are}\ Q(2k, 2m)\Rightarrow\ Q(2m^3,2m)\)

Calculus, MET1 SM-Bank 3

For the function  `f:R→R,\ \ f(x)= 2e^x + 3x`, determine the coordinates of the point  `P`  at which the tangent to  `f(x)`  is parallel to the line  `y = 5x - 3`.   (3 marks)

Show Answers Only

`(0, 2)`

Show Worked Solution

`y = 5x-3\ \ =>\ m=5`

`y` `= 2e^x + 3x`
`(dy)/(dx)` `= 2e^x + 3`

  
`text(Find)\ \ x\ \ text(when)\ \ (dy)/(dx) = 5,`

`5` `= 2e^x + 3`
`2e^x` `= 2`
`e^x` `= 1`
`x` `= 0`

  
`text(When)\ \ x = 0,`

`y` `= 2e^0 + (3 xx 0)=2`

  
`:.P\ \ text{has coordinates (0, 2)}`

Calculus, MET2 2016 VCAA 2

Consider the function  `f(x) = -1/3 (x + 2) (x-1)^2.`

  1.  i. Given that  `g^{′}(x) = f (x) and g (0) = 1`,
  2.      show that  `g(x) = -x^4/12 + x^2/2-(2x)/3 + 1`.   (1 mark)

  3. ii. Find the values of `x` for which the graph of  `y = g(x)`  has a stationary point.   (1 mark)

The diagram below shows part of the graph of  `y = g(x)`, the tangent to the graph at  `x = 2`  and a straight line drawn perpendicular to the tangent to the graph at  `x = 2`. The equation of the tangent at the point `A` with coordinates  `(2, g(2))`  is  `y = 3-(4x)/3`.

The tangent cuts the `y`-axis at `B`. The line perpendicular to the tangent cuts the `y`-axis at `C`.
 


 

  1.   i. Find the coordinates of `B`.   (1 mark)

  2.  ii. Find the equation of the line that passes through `A` and `C` and, hence, find the coordinates of `C`.   (2 marks)

  3. iii. Find the area of triangle `ABC`.   (2 marks)

  4. The tangent at `D` is parallel to the tangent at `A`. It intersects the line passing through `A` and `C` at `E`.

     


     
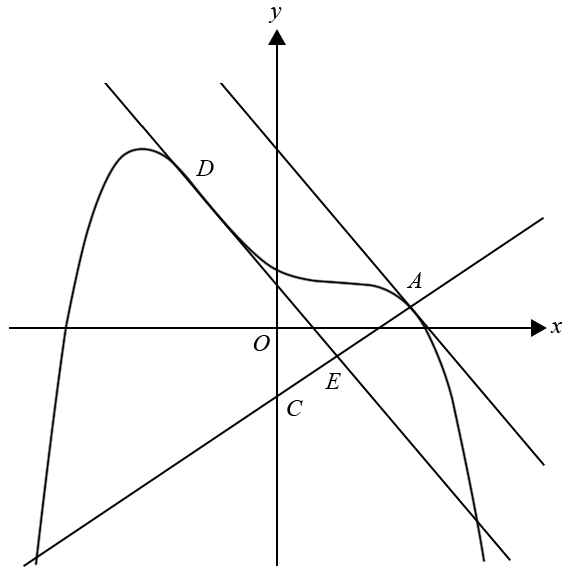
     i. Find the coordinates of `D`.   (2 marks)

  5. ii. Find the length of `AE`.   (3 marks)

Show Answers Only
  1.  i. `text(Proof)\ \ text{(See worked solutions)}`
  2. ii. `x = -2, 1`
  3.   i. `(0, 3)`
  4. ii. `y = 3/4 x-7/6`
  5.      `(0, -7/6)`
  6. iii. `25/6\ text(u²)`
  7. `(-1, 25/12)`
  8. `27/20\ text(u)`
Show Worked Solution
a.i.    `g(x)` `= int f(x)\ dx`
    `=-1/3 int (x + 2) (x-1)^2\ dx`
    `=-1/3int(x^3-3x+2)\ dx`
  `:.g(x)` `= -x^4/12 + x^2/2-(2x)/3 + c`

 
`text(S)text(ince)\ \ g(0) = 1,`

`1` `= 0 + 0-0 + c`
`:. c` `= 1`

  
`:. g(x) = -x^4/12 + x^2/2-(2x)/3 + 1\ \ …\ text(as required)`
 

a.ii.   `text(Stationary point when:)`

`g^{′}(x) = f(x) = 0`

`-1/3(x + 2) (x-1)^2=0`

`:. x = -2, 1`
 

b.i.   

`B\ text(is the)\ y text(-intercept of)\ \ y = 3-4/3 x`

`:. B (0, 3)`
 

b.ii.   `m_text(norm) = 3/4, \ text(passes through)\ \ A(2, 1/3)`

   `text(Equation of normal:)`

`y-1/3` `=3/4(x-2)`
`y` `=3/4 x-7/6`
   

`:. C (0, -7/6)`
 

b.iii.   `text(Area)` `= 1/2 xx text(base) xx text(height)`
    `= 1/2 xx (3 + 7/6) xx 2`
    `= 25/6\ text(u²)`

 

♦ Mean mark part (c)(i) 43%.
MARKER’S COMMENT: Many students gave an incorrect `y`-value here. Be careful!
c.i.    `text(Solve)\ \ \ g^{′}(x)` `= -4/3\ \ text(for)\ \ x < 0`
  `=> x` `= -1`
  `g(-1)` `=-1/12+1/2+2/3+1`
    `=25/12`

  
`:. D (−1, 25/12)`
 

c.ii.   `text(T) text(angent line at)\ \ D:`

`y-25/12` `=-4/3(x+1)`
`y` `=-4/3x + 3/4`

 
`DE\ \ text(intersects)\ \ AE\ text(at)\ E:`

♦♦ Mean mark 32%.
`-4/3 x + 3/4` `= 3/4 x-7/6`
`25/12 x` `= 23/12`
`x` `=23/25`

 
`:. E (23/25, -143/300)`
 

`:. AE` `= sqrt((2-23/25)^2 + (1/3-(-143/300))^2)`
  `= 27/20\ text(units)`

Calculus, MET2 2016 VCAA 10 MC

For the curve  `y = x^2 - 5`, the tangent to the curve will be parallel to the line connecting the positive x-intercept and the y-intercept when `x` is equal to

A.   `sqrt 5`

B.   `5`

C.   `−5`

D.   `sqrt 5/2`

E.   `1/sqrt 5`

Show Answers Only

`D`

Show Worked Solution

`text{Intercepts: (0, −5) and}\ (sqrt 5, 0)`

`text(Gradient between intercepts:)`

`m = (0 – (−5))/(sqrt 5 – 0) = 5/sqrt 5`

`text(Solve:)`

`f prime (x)` `= 5/sqrt 5`
`2x` `= 5/sqrt 5`
`:. x` `=5/(2sqrt5) xx sqrt5/sqrt5`
  `= sqrt 5/2`

 
`=>   D`

Calculus, MET1 2015 VCAA 10

The diagram below shows a point, `T`, on a circle. The circle has radius 2 and centre at the point `C` with coordinates `(2, 0)`. The angle `ECT` is `theta`, where  `0 < theta <= pi/2`.
  

met1-2015-vcaa-q10
  

The diagram also shows the tangent to the circle at `T`. This tangent is perpendicular to `CT` and intersects the `x`-axis at point `X` and the `y`-axis at point `Y`.

  1. Find the coordinates of `T` in terms of `theta`.   (1 mark)

  2. Find the gradient of the tangent to the circle at `T` in terms of `theta`.   (1 mark)

  3. The equation of the tangent to the circle at `T` can be expressed as
  4. `qquad cos(theta)x + sin(theta)y = 2 + 2cos(theta)`
  5.  i. Point `B`, with coordinates `(2, b)`, is on the line segment `XY`.
  6.     Find `b` in terms of `theta`.   (1 mark)

  7. ii. Point `D`, with coordinates `(4, d)`, is on the line segment `XY`.
  8.     Find `d` in terms of `theta`.   (1 mark)

  9. Consider the trapezium `CEDB` with parallel sides of length `b` and `d`.
  10. Find the value of `theta` for which the area of the trapezium `CEDB` is a minimum. Also find the minimum value of the area.   (3 marks)

Show Answers Only
  1. `T(2 + 2costheta, 2 sintheta)`
  2. `(-1)/(tan(theta))`
  3.  i. `2/(sintheta)`
  4. ii. `(2-2 costheta)/(sintheta)`
  5. `theta = pi/3`
  6. `A_text(min) = 2sqrt3\ text(u²)`
Show Worked Solution
a.    `cos theta` `= (CM)/(CT)`
    `=(CM)/2`
  `CM` `= 2costheta`
♦♦♦ Part (a) mean mark 20%.
MARKER’S COMMENT: Many students did not include the “+2” in the `x`-coordinate.
`sintheta` `= (TM)/2`
`TM` `= 2sintheta`

 

`:. T\ text(has coordinates)\ \ (2 + 2costheta, 2 sintheta)`

 

♦♦♦ Part (b) mean mark 16%.
b.    `m_(CT)` `=(TM)/(CM)`
    `=(2 sin theta)/(2 cos theta)`
    `=tan theta`
     
  `:.m_(XY)` `=-1/tan theta,\ \ \ (CT ⊥ XY)`

 

c.i.   `text(Substitute)\ \ (2,b)\ \ text(into equation:)`

`2costheta + bsintheta` `= 2 + 2costheta`
`:. b` `= 2/(sintheta)`

 

c.ii.   `text(Substitute)\ \ (4,d)\ \ text(into equation:)`

♦ Part (c)(ii) mean mark 47%.
`4costheta + dsintheta` `= 2 + 2costheta`
`d sin theta` `=2-cos theta`
`:.d`  `= (2-2 costheta)/(sintheta)`

 

♦♦♦ Part (d) mean mark 19%.
d.    `text(A)_text(trap)` `= 1/2 xx 2 xx (b + d)`
    `= 2/(sintheta) + (2-2costheta)/(sintheta)`
    `= (4-2costheta)/(sintheta)`

 

`text(Stationary point when)\ \ (dA)/(d theta)=0`

`(2sin^2theta-costheta(4-2costheta))/(sin^2theta)` `= 0`
`2sin^2theta-4costheta + 2cos^2theta` `= 0`
`2[sin^2theta + cos^2theta]-4costheta` `= 0`
`2-4costheta` `= 0`
`costheta` `= 1/2`
`theta` `= pi/3,\ \ \ \ theta ∈ (0, pi/2)`

 

`A(pi/3)` `= (4-2(1/2))/(sqrt3/2)`
  `=3 xx 2/sqrt3`
  `= 2sqrt3`

 

`:. A_text(min) = 2sqrt3\ text(u²)`