SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, MET1 2024 VCAA 3

Let  \(g: R \backslash\{-3\} \rightarrow R, \ g(x)=\dfrac{1}{(x+3)^2}-2\).

  1. On the axes below, sketch the graph of  \(y=g(x)\),  labelling all asymptotes with their equations and axis intercepts with their coordinates.   (3 marks)


  2. Determine the area of the region bounded by the line  \(x=-2\),  the \(x\)-axis, the \(y\)-axis and the graph of \(y=g(x)\).   (2 marks)

Show Answers Only

a.

b.    \(\dfrac{10}{3}\ \text{sq units}\)

Show Worked Solution

a.    \(y\text{-intercept:}\ x=0\)

\(y=\dfrac{1}{(0+3)^2}-2=-\dfrac{17}{9}\)

\(x\text{-intercepts:}\ y=0\)

\(\dfrac{1}{(x+3)^2}-2\) \(=0\)
\((x+3)^2\) \(=\dfrac{1}{2}\)
\(x+3\) \(=\pm\dfrac{1}{\sqrt{2}}\)
\(x\) \(=-3\pm\dfrac{1}{\sqrt{2}}\)

b.   \(\text{Area is below}\ x\text{-axis:}\)

  \(\text{Area}\) \(=-\displaystyle\int_{-2}^0 (x+3)^{-3}-2\,dx\)
    \(=-\left[\dfrac{1}{-1}(x+3)^{-1}-2x\right]_{-2}^0\)
    \(=-\left[\dfrac{-1}{x+3}-2x\right]_{-2}^0\)
    \(=-\left[\dfrac{-1}{3}-\left(\dfrac{-1}{-2+3}-2(-2)\right)\right]\)
    \(=-\Big[\dfrac{-1}{3}-(-1+4)\Big] \)
    \(=\dfrac{10}{3}\ \text{u}^{2}\)
♦ Mean mark (b) 40%.

Calculus, MET1 2019 VCAA 5

Let  `f: R\ text(\{1}) -> R, \ f(x) = 2/(x-1)^2 + 1`.

    1. Evaluate  `f(-1)`.   (1 mark)

    2. Sketch the graph of `f` on the axes below, labelling all asymptotes with their equations.   (2 marks)

        

  2. Find the area bounded by the graph of `f`, the `x`-axis, the line  `x = -1`  and the line  `x = 0`.   (2 marks)

Show Answers Only
    1. `3/2`
    2. `text(See Worked Solutions)`
  2. `2`
Show Worked Solution
a.i.    `f(-1)` `= 2/(-1-1)^2 + 1`
    `= 3/2`

​

a.ii.     

 

b.    `text(Area)` `= int_(-1)^0 2/(x-1)^2 + 1\ dx`
    `= int_(-1)^0 2(x-1)^(-2) + 1\ dx`
    `= [-2(x-1)^(-1) + x]_(-1)^0`
    `= [((-2)/-1 + 0)-((-2)/-2-1)]`
    `= 2`

Calculus, MET1 2016 VCAA 3

Let  `f: R text{\}{1} -> R`  where  `f(x) = 2 + 3/(x - 1)`.

  1. Sketch the graph of  `f`. Label the axis intercepts with their coordinates and label any asymptotes with the appropriate equation.   (3 marks)
     

     

  2. Find the area enclosed by the graph of  `f`, the lines  `x = 2`  and  `x = 4`, and the `x`-axis.   (2 marks)

Show Answers Only
  1.  
  2. `4 + 3log_e(3)\ text(units)`
Show Worked Solution
a.   

 

b.    `text(Area)` `= int_2^4 2 + 3(x – 1)^(−1)\ dx`
    `= [2x + 3 log_e(x – 1)]_2^4`
    `= (8 + 3log_e(3)) – (4 + 3log_e(1))`
    `= 4 + 3log_e(3)\ \ text(u²)`

Calculus, MET2 2016 VCAA 4

  1. Express  `(2x + 1)/(x + 2)`  in the form  `a + b/(x + 2)`,  where `a` and `b` are non-zero integers.   (2 marks)

  2. Let  `f: R text(\){−2} -> R,\ f(x) = (2x + 1)/(x + 2)`.
    1. Find the rule and domain of `f^(-1)`, the inverse function of `f`.   (2 marks)

    2. Part of the graphs of `f` and  `y = x`  are shown in the diagram below.
       

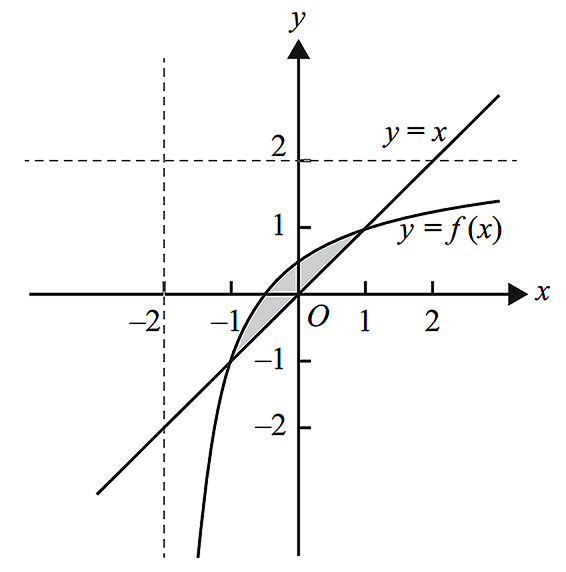
    3. Find the area of the shaded region.   (1 mark)

    4. Part of the graphs of `f` and `f^(-1)` are shown in the diagram below.
       

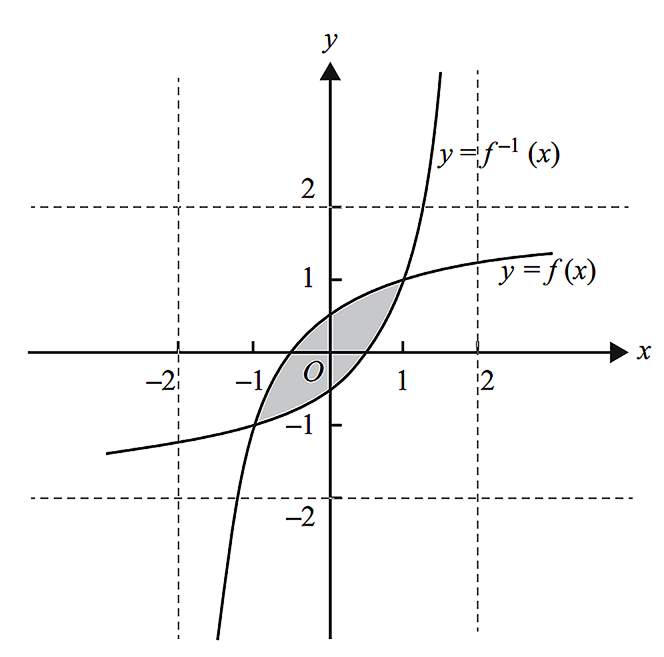
    5. Find the area of the shaded region.   (1 mark) 
  1. Part of the graph of `f` is shown in the diagram below.
     
       
     

     

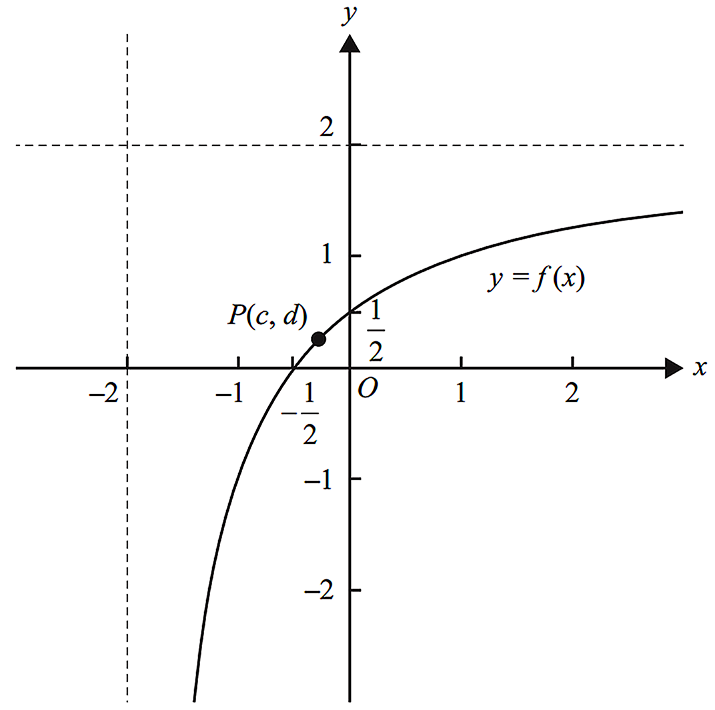
    The point `P(c, d)` is on the graph of `f`.

     

    Find the exact values of `c` and `d` such that the distance of this point to the origin is a minimum, and find this minimum distance.   (3 marks)

Let  `g: (−k, oo) -> R, g(x) = (kx + 1)/(x + k)`, where `k > 1`.

  1. Show that  `x_1 < x_2`  implies that  `g(x_1) < g(x_2),` where  `x_1 in (−k, oo) and x_2 in (−k, oo)`.   (2 marks)

  2. Let `X` be the point of intersection of the graphs of  `y = g (x) and y = −x`.
    1. Find the coordinates of `X` in terms of `k`.   (2 marks)

    2. Find the value of `k` for which the coordinates of `X` are  `(-1/2, 1/2)`.   (2 marks)

    3. Let  `Ztext{(− 1, − 1)}, Y(1, 1)`  and `X` be the vertices of the triangle `XYZ`. Let  `s(k)`  be the square of the area of triangle `XYZ`.
       

       

         
       

       

      Find the values of `k` such that  `s(k) >= 1`.   (2 marks)

  3. The graph of `g` and the line  `y = x`  enclose a region of the plane. The region is shown shaded in the diagram below.
     

     

     

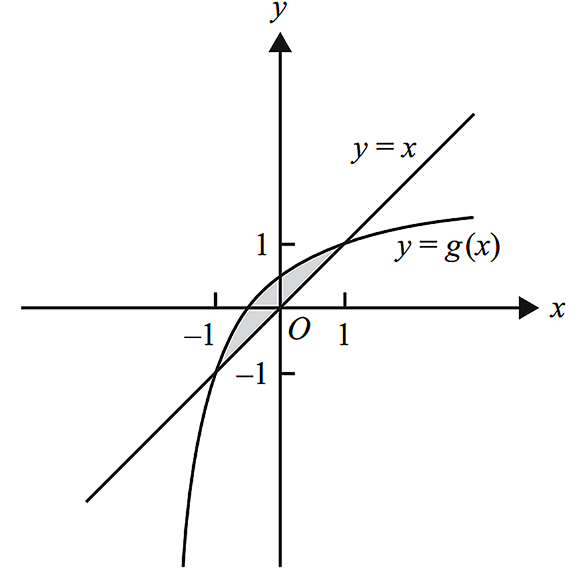
    Let  `A(k)`  be the rule of the function `A` that gives the area of this enclosed region. The domain of `A` is  `(1, oo)`.

    1. Give the rule for `A(k)`.   (2 marks)

    2. Show that  `0 < A(k) < 2`  for all  `k > 1`.   (2 marks)

Show Answers Only
  1. `2 + {(−3)}/(x + 2)`
  2.   i. `f^(-1) (x) = (-3)/(x-2)-2,\ \ x in R text(\){2}`
  3.  ii. `4-3 ln(3)\ text(units²)`
  4. iii. `8-6 log_e (3)\ text(units²)`
  5. `c = sqrt 3-2, \ d = 2-sqrt 3`
  6. `text(min distance) = (2 sqrt 2-sqrt 6)`
  7. `text(Proof)\ \ text{(See Worked Solutions)}`
  8.   i. `X (−k + sqrt (k^2-1), k-sqrt (k^2-1))`
  9.  ii. `k = 5/4`
  10. iii. `k in (1, 5/4]`
  11.  i. `A(k) = (k^2-1) log_e ((k-1)/(k + 1)) + 2k`
  12. ii. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

a.   `text(Solution 1)`

`(2x + 1)/(x + 2)` `= 2-3/(x + 2)`
  `= 2 + {(-3)}/(x + 2) qquad [text(CAS: prop Frac) ((2x + 1)/(x + 2))]`

 

`text(Solution 2)`

`(2x + 1)/(x + 2)` `=(2(x+2)-3)/(x+2)`
  `=2+ (-3)/(x+2)`

 

b.i.  `text(Let)\ \ y = f(x)`

`text(For Inverse: swap)\ \ x ↔ y`

`x` `=2-3/(y + 2)`
`(x-2)(y+2)` `=-3`
`y` `=(-3)/(x-2)-2`

 

`text(Range of)\ f(x):\ \ y in R text(\){2}`

`:. f^(-1) (x) = (-3)/(x-2)-2, \ x in R text(\){2}`

 

b.ii.   `text(Find intersection points:)`

`f(x)` `= x`
`(2x+1)/(x+2)` `=x`
`2x+1` `=x^2+2x`
`:. x` `= +- 1`
`:.\ text(Area)` `= int_(-1)^1 (f(x)-x)\ dx`
  `=int_(-1)^1 (2-3/(x + 2)-x)\ dx`
  `= 4-3 ln(3)\ text(u²)`

 

b.iii.    `text(Area)` `= int_(-1)^1 (f(x)-f^(-1) (x)) dx`
    `=2 xx (4-3 ln(3))\ \ \ text{(twice the area in (b)(ii))}`
    `= 8-6 log_e (3)\ text(u²)`
♦♦♦ Mean mark part (c) 25%.

 

c.   
  `text(Let)\ \ z` `= OP, qquad P(c, -3/(c + 2) + 2)`
  `z` `= sqrt (c^2 + (2-3/(c + 2))^2), \ c > -2`

`text(Stationary point when:)`

`(dz)/(dc) = 0, c > -2`

`:.\ c = sqrt 3-2 overset and (->) d = 2-sqrt 3`

`:. text(Minimum distance) = (2 sqrt 2-sqrt 6)`

 

d.   `text(Given:)\ \ -k < x_1 < x_2`

♦♦♦ Mean mark part (d) 8%.

`text(Must prove:)\ \ g(x_2)-g(x_1) > 0`

`text(LHS:)`

`g(x_2)-g(x_1)`

`= (kx_2 +1)/(x_2+k)-(kx_1 +1)/(x_1+k)`

`=((kx_2 +1)(x_1+k)-(kx_1 +1)(x_2+k))/((x_2+k)(x_1+k))`

`=(k^2(x_2-x_1)-(x_2-x_1))/((x_2+k)(x_1+k))`

`=((k^2-1)(x_2-x_1))/((x_2+k)(x_1+k))`

 

`x_2-x_1 >0,\ and \ k^2-1>0`

`text(S)text(ince)\ \ x_2>x_1> -k,`

`=> -x_2<-x_1<k`

`=>k+x_1 >0, \ and \ k+x_2>0`

 

`:.g(x_2)-g(x_1) >0`

`:. g(x_2) > g(x_1)`

 

♦♦ Mean mark part (e)(i) 32%.
e.i.    `g(x)` `= -x`
  `(kx +1)/(x+k)` `=-x`
  `kx+1` `=-x^2-xk`
  `x^2+2k+1` `=0`
  `:. x` `=(-2k +- sqrt(4k^2-4))/2`
    `= sqrt (k^2-1)-k\ \ text(for)\ \ x > -k`

 

`:. X (-k + sqrt(k^2-1),\ \ k-sqrt(k^2-1))`

 

e.ii.   `text(Equate)\ \ x text(-coordinates:)`

♦ Mean mark part (e)(ii) 44%.
`-k + sqrt(k^2-1)` `= -1/2`
`sqrt(k^2-1)` `=k-1/2`
`k^2-1` `=k^2-k+1/4`
`:. k` `= 5/4`

 

e.iii.   `s(k)` `= (1/2 xx YZ xx XO)^2`
    `= 1/4 xx (YZ)^2 xx (XO)^2`

 

`ZO = sqrt(1^2+1^2) = sqrt2`

♦♦♦ Mean mark (e)(iii) 6%.

`YZ=2 xx ZO = 2sqrt2`

`(YZ)^2 = 8`

`(XO)^2` `=(-k + sqrt(k^2-1))^2-(k-sqrt (k^2-1))^2`
  `=2(-k + sqrt(k^2-1))^2`
   

 `text(Solve)\ \ s(k) >= 1\ \ text(for)\ \ k >= 1,`

`1/4 xx 8 xx 2(-k + sqrt(k^2-1))^2` `>=1`
`(-k + sqrt(k^2-1))^2` `>=1/4`
`k-sqrt(k^2-1)` `>=1/2`
`k-1/2` `>= sqrt(k^2-1)`
`k^2-k+1/4` `>=k^2-1`
`:.k` `<= 5/4`

`:.  1<k<= 5/4`

 

♦♦ Mean mark (f)(i) 28%.
f.i.    `A(k)` `= int_(-1)^1 (g(x)-x)\ dx,\ \ k > 1`
    `= int_(-1)^1 ((kx+1)/(x+k) -x)\ dx`
    `= int_(-1)^1 (k+ (1-k^2)/(x+k) -x)`
    `=[kx + (1-k^2) log_e(x+k)-x^2/2]_(-1)^1`
    `=(k+(1-k^2)log_e(1+k)-1/2)-(-k+(1-k^2)log_e(k-1)-1/2)`
    `=2k+(1-k^2)log_e ((1+k)/(k-1))`
    `= (k^2-1) log_e ((k-1)/(k + 1)) + 2k`

 

♦♦♦ Mean mark part (f)(ii) 4%.
f.ii.  
  `0` `< A(k) < text(Area of)\ Delta ABC`
  `0` `< A(k) < 1/2 xx AC xx BO`
  `0` `< A(k) < 1/2 sqrt(2^2 + 2^2) xx (sqrt(1^2 + 1^2))`
  `0` `< A(k) < 1/2 xx 2 sqrt 2 xx sqrt 2`
  `:. 0` `< A(k) < 2`