SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, MET1 2024 VCAA 7

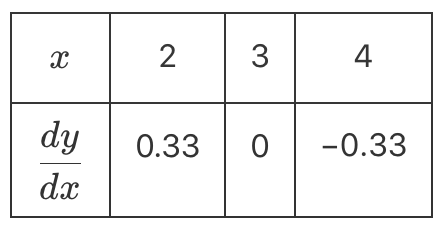
Part of the graph of  \(f:[-\pi, \pi] \rightarrow R, f(x)=x \sin (x)\)  is shown below.

  1. Use the trapezium rule with a step size of \(\dfrac{\pi}{3}\) to determine an approximation of the total area between the graph of  \(y=f(x)\) and the \(x\)-axis over the interval  \(x \in[0, \pi]\).   (3 marks)

  2.   i. Find \(f^{\prime}(x)\).   (1 mark)

  3.  ii. Determine the range of \(f^{\prime}(x)\) over the interval \(\left[\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right]\).   (1 mark)

  4. iii. Hence, verify that \(f(x)\) has a stationary point for \(x \in\left[\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right]\).   (1 mark)

  5. On the set of axes below, sketch the graph of  \(y=f^{\prime}(x)\)  on the domain \([-\pi, \pi]\), labelling the endpoints with their coordinates.
  6. You may use the fact that the graph of  \(y=f^{\prime}(x)\)  has a local minimum at approximately \((-1.1,-1.4)\) and a local maximum at approximately \((1.1,1.4)\).   (3 marks)

Show Answers Only

a.    \(\dfrac{\sqrt{3}\pi^2}{6}\)

bi.   \(x\cos(x)+\sin(x)\)

bii.  \(\left[-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3},\ 1\right]\)

biii. \(\text{In the interval }\left[\dfrac{\pi}{2}, \dfrac{2\pi}{3}\right],\ f^{\prime}(x)\ \text{changes from positive to negative.}\)

\(f^{\prime}(x)=0\ \text{at some point in the interval.}\)

\(\therefore\ \text{A stationary point must exist in the given range.}\)

c. 

Show Worked Solution

a.     \(A\) \(=\dfrac{\pi}{3}\times\dfrac{1}{2}\left(f(0)+2f\left(\dfrac{\pi}{3}\right)+2f\left(\dfrac{2\pi}{3}\right)+f(\pi)\right)\)
    \(=\dfrac{\pi}{6}\left(0+2\times \dfrac{\pi}{3}\sin\left(\dfrac{\pi}{3}\right)+2\times \dfrac{2\pi}{3}\sin\left(\dfrac{2\pi}{3}\right)+\pi\sin({\pi})\right)\)
    \(=\dfrac{\pi}{6}\left(2\times \dfrac{\pi}{3}\times\dfrac{\sqrt{3}}{2}+2\times\dfrac{2\pi}{3}\times \dfrac{\sqrt{3}}{2}+0\right)\)
    \(=\dfrac{\pi}{6}\left(\dfrac{2\pi\sqrt{3}}{6}+\dfrac{4\pi\sqrt{3}}{6}\right)\)
    \(=\dfrac{\pi}{6}\times \dfrac{6\pi\sqrt{3}}{6}\)
    \(=\dfrac{\sqrt{3}\pi^2}{6}\)
♦ Mean mark (a) 48%.
bi.    \(f(x)\) \(=x\sin(x)\)
  \(f^{\prime}(x)\) \(=x\cos(x)+\sin(x)\)

 

b.ii.  \(\text{Gradient in given range gradually decreases.}\)

\(\text{Range of}\ f^{\prime}(x)\ \text{will be defined by the endpoints.}\)

  \(f^{\prime}\left(\dfrac{\pi}{2}\right)\) \(=1\)
  \(f^{\prime}\left(\dfrac{2\pi}{3}\right)\) \(=\dfrac{2\pi}{3}\left(\dfrac{-1}{2}+\dfrac{\sqrt{3}}{2}\right)=-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3}\)

 
\(\therefore\ \text{Range of }\ f^{\prime} (x)\ \text{is}\quad\left[-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3},\ 1\right]\)

♦♦♦ Mean mark (b.ii.) 20%.
♦♦♦ Mean mark (b.iii.) 12%.

 
biii. \(\text{In the interval }\left[\dfrac{\pi}{2}, \dfrac{2\pi}{3}\right],\ f^{\prime}(x)\ \text{changes from positive to negative.}\)

\(f^{\prime}(x)=0\ \text{at some point in the interval.}\)

\(\therefore\ \text{A stationary point must exist in the given range.}\)

 
c.    \(f^{\prime}(\pi)=\pi\cos(\pi)+\sin(\pi)=-\pi\)

\(f^{\prime}(-\pi)=-\pi\cos(-\pi)+\sin(-\pi)=\pi\)

\(\therefore\ \text{Endpoints are }\ (-\pi,\ \pi)\ \text{and}\ (\pi,\ -\pi).\)

♦♦ Mean mark (c) 36%.

Calculus, MET2 2024 VCAA 15 MC

The points of inflection of the graph of  \(y=2-\tan \left(\pi\left(x-\dfrac{1}{4}\right)\right)\)  are

  1. \(\left(k+\dfrac{1}{4}, 2\right), k \in Z\)
  2. \(\left(k-\dfrac{1}{4}, 2\right), k \in Z\)
  3. \(\left(k+\dfrac{1}{4},-2\right), k \in Z\)
  4. \(\left(k-\dfrac{3}{4},-2\right), k \in Z\)
Show Answers Only

\(A\)

Show Worked Solution

\(\text{The graph of}\ \ y=-\tan(\pi x)\ \text{is translated 2 units upwards and then}\)

\(\text{translated }\dfrac{1}{4}\ \text{units to the right to become the graph shown below.}\)

\(\text{Hence all points of inflection lie of the line}\ y=2\)

\(\rightarrow\ \text{Eliminate Options C and D}\)
 

\(\text{Consider Option A:}\)

\(\text{When}\ \ k=0, x=0+\dfrac{1}{4}=\dfrac{1}{4}\)

\(\text{then}\ \ y=2-\tan \left(\pi\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\right)=2\)

\(\text{Similarly for any}\ k \in Z\ \text{a point of inflection will be found at }\ \left(k+\dfrac{1}{4}, 2\right)\)

\(\Rightarrow A\)

Functions, MET2 2023 VCAA 9 MC

The function \(f\) is given by
 

\(f(x) = \begin {cases}
\tan\Bigg(\dfrac{x}{2}\Bigg)         &\ \ 4 \leq x \leq 2\pi \\
\sin(ax) &\ \ \ 2\pi\leq x\leq 8
\end{cases}\)

 
The value of \(a\) for which \(f\) is continuous and smooth at  \( x\) = \(2\pi\)  is

  1. \(-2\)
  2. \(-\dfrac{\pi}{2}\)
  3. \(-\dfrac{1}{2}\)
  4. \(\dfrac{1}{2}\)
  5. \(2\)
Show Answers Only

\(C\)

Show Worked Solution

\(\text{Solve for}\ a\ \text{given}\ \ x=2\pi:\)

\(\tan\Bigg(\dfrac{2\pi}{2}\Bigg)=\sin(a2\pi)=0\)

\(a=\pm \dfrac{1}{2}\)
 

\(\text{For smoothness, solve for}\ a\ \text{given}\ \ x=2\pi:\)

\(\dfrac{d}{dx}\tan\Bigg(\dfrac{x}{2}\Bigg)=\dfrac{d}{dx}\sin(ax)\)

\(\therefore a=-\dfrac{1}{2}\)

 
\(\Rightarrow C\)


♦ Mean mark 46%.

Calculus, MET1 2021 VCAA 8

The gradient of a function is given by  `(dy)/(dx) = sqrt(x + 6)-x/2-3/2`.

The graph of the function has a single stationary point at  `(3, 29/4)`.

  1. Find the rule of the function.   (3 marks)

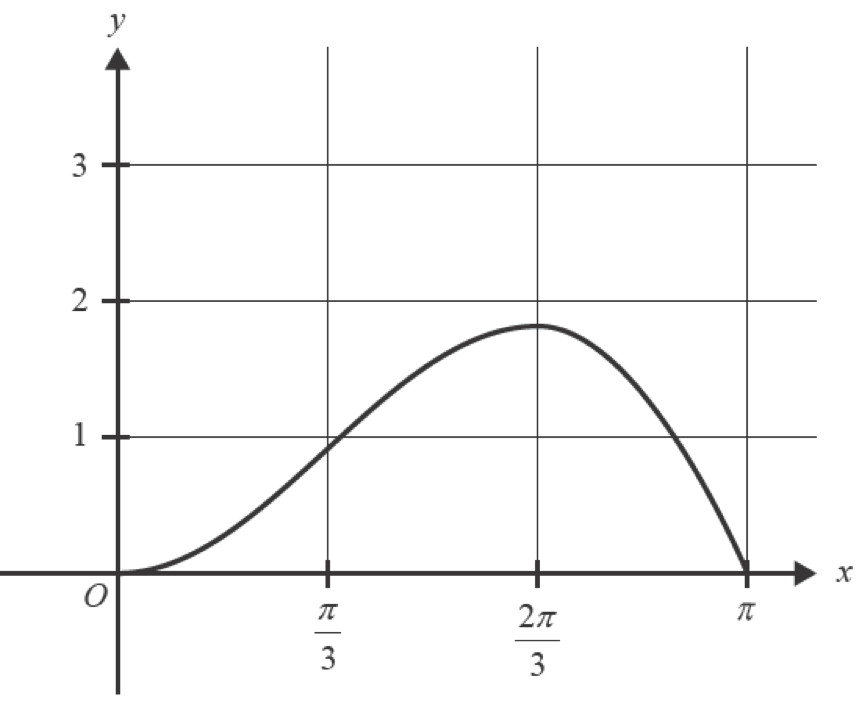
  2. Determine the nature of the stationary point.   (2 marks)

Show Answers Only
  1. `y=2/3(x+6)^(3/2)-x^2/4-3/2x-4`
  2. `text{Maximum}`
Show Worked Solution
a.    `dy/dx` `= sqrt(x + 6)-x/2-3/2`
  `y` `=int sqrt(x + 6)-x/2-3/2\ dx`
    `=2/3(x+6)^(3/2)-x^2/4-3/2x + c`

 
`text{Graph passes through}\ (3, 29/4)`

`29/4` `=2/3*9^(3/2)-3^2/4-3/2 * 3+c`  
`29/4` `=18-9/4-9/2+c`  
`c` `=29/4-18+9/4+9/2`  
  `=-4`  

 
`:. y=2/3(x+6)^(3/2)-x^2/4-3/2x-4`

♦ Mean mark part (b) 37%.

b. 
      

`:.(3,29/4)\ text{is a maximum}.`

Graphs, MET2 2015 VCAA 7 MC

The range of the function  `f:\ text{(−1, 2]} -> R,\ \ f(x) = -x^2 + 2x-3` is

  1. `R`
  2. `text{(−6, −3]}`
  3. `text{(−6, −2]}`
  4. `text{[−6, −3]}`
  5. `text{[−6, −2]}`
Show Answers Only

`C`

Show Worked Solution

`text(A sketch of the equation:)`

`y` `=-x^2 + 2x-3`
 `dy/dx` `=-2x+2`

 

`=>\ text(Concave down with turning point when)\ \ x=1,`
 

vcaa-2015-7mc-answer1
 

`:. text(Range) = (-6,-2]`

`=>   C`