SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Graphs, MET2 2022 VCAA 9 MC

Let `f:[0, \infty) \rightarrow R, f(x)=\sqrt{2 x+1}`.

The shortest distance, `d`, from the origin to the point `(x, y)` on the graph of `f` is given by

  1. `d=x^2+2 x+1`
  2. `d=x^2+\sqrt{2 x+1}`
  3. `d=\sqrt{x^2-2 x+1}`
  4. `d=x+1`
  5. `d=2 x+1`
Show Answers Only

`D`

Show Worked Solution

Straight line distance is the shortest.

`:.` Therefore, using pythagoras and given `f(x) = \sqrt{2x+1}` 

`d^2` `= x^2 + y^2`  
  `=x^2 + (sqrt{2x+1})^2`  
  `= x^2 + 2x +1`  
  `=(x + 1)^2`  
`d` `=sqrt((x + 1)^2)`  
  `= x+1`  

  
`=>D`


♦ Mean mark 50%.

Calculus, MET2 2017 VCAA 1

Let  `f : R → R,\  f (x) = x^3 - 5x`. Part of the graph of  `f` is shown below.

 

  1. Find the coordinates of the turning points.  (2 marks)
  2. `A(−1, f (−1))`  and  `B(1, f (1))`  are two points on the graph of  `f`.

     

    1. Find the equation of the straight line through `A` and `B`.  (2 marks)
    2. Find the distance `AB`.  (1 mark)

Let  `g : R → R, \ g(x) = x^3 - kx, \ k ∈ R^+`.

  1. Let  `C(–1, g(−1))` and `D(1, g(1))` be two points on the graph of `g`.

     

    1. Find the distance `CD` in terms of `k`.  (2 marks)
    2. Find the values of `k` such that the distance `CD` is equal to  `k + 1`.  (1 mark)
  2. The diagram below shows part of the graphs of `g` and  `y = x`. These graphs intersect at the points with the coordinates `(0, 0)` and `(a, a)`.
  3.  
  4.  
    1. Find the value of `a` in terms of `k`.  (1 mark)
    2. Find the area of the shaded region in terms of `k`.  (2 marks)
Show Answers Only
  1. `(- sqrt15/3,(10sqrt15)/9)\ text(and)\ (sqrt15/3,-(10sqrt15)/9)`
    1. `y =-4x`
    2. `2sqrt17`
    1. `2sqrt(k^2 – 2k + 2)`
    2. `k = 1quadtext(or)quadk = 7/3`
    1. `sqrt(k + 1)`
    2. `((k + 1)^2)/4\ text(units)²`
Show Worked Solution
a.   
`text(Solve)\ \ f′(x)` `= 0\ \ text(for)\ x:`
`x` `= ± sqrt15/3`

 

`f(sqrt15/3) = -(10sqrt15)/9`

`f(−sqrt15/3) = (10sqrt15)/9`

 

`:.\ text(Turning points:)`

`(- sqrt15/3,(10sqrt15)/9)\ text(and)\ (sqrt15/3,-(10sqrt15)/9)`

 

b.i.   `A(-1,4),\ \ B(1,–4)`

`m_(AB) = (4 – (−4))/(−1 – (1)) = −4`

 

`text(Equation of)\ AB, m=-4, text(through)\ \ (-1,4):`

` y – 4` `= −4(x – (−1))`
`:. y` `= −4x`

 

MARKER’S COMMENT: Students skilled in the use of technology will be much more efficient and minimise errors here.
b.ii.    `d_(text(AB))` `=sqrt((x_2-x_1)^2+(f(x_2)-f(x_1))^2)`
    `= sqrt((1- (- 1))^2 + (f(1) – f(−1))^2)`
    `= 2sqrt17`

 

c.i.    `d_(text(CD))` `=sqrt((x_2-x_1)^2+(g(x_2)-g(x_1))^2)`
    `=sqrt((1-(-1))^2+(g(1)-g(-1))^2)`
    `= 2sqrt(k^2 – 2k + 2)`

 

c.ii.   `text(Solve:)quad2sqrt(k^2 – 2k + 2) = k + 1quadtext(for)quadk > 0`

`:. k = 1quadtext(or)quadk = 7/3`

 

d.i.   `text(Solve:)quada^3 – ka = a\ \ \ text(for)quad a,\ \ (a > 0)`

`:. a = sqrt(k + 1)`

 

d.ii.    `text(Area)` `= int_0^(sqrt(k + 1))(x – g(x))\ dx`
    `= ((k + 1)^2)/4\ text(units)²`

Calculus, MET2 2016 VCAA 2

Consider the function  `f(x) = -1/3 (x + 2) (x-1)^2.`

  1.  i. Given that  `g^{′}(x) = f (x) and g (0) = 1`, show that  `g(x) = -x^4/12 + x^2/2-(2x)/3 + 1`.  (1 mark)
  2. ii. Find the values of `x` for which the graph of  `y = g(x)`  has a stationary point.  (1 mark)

The diagram below shows part of the graph of  `y = g(x)`, the tangent to the graph at  `x = 2`  and a straight line drawn perpendicular to the tangent to the graph at  `x = 2`. The equation of the tangent at the point `A` with coordinates  `(2, g(2))`  is  `y = 3-(4x)/3`.

The tangent cuts the `y`-axis at `B`. The line perpendicular to the tangent cuts the `y`-axis at `C`.
 


 

  1.   i. Find the coordinates of `B`.  (1 mark)
  2.  ii. Find the equation of the line that passes through `A` and `C` and, hence, find the coordinates of `C`.  (2 marks)
  3. iii. Find the area of triangle `ABC`.  (2 marks)
  4. The tangent at `D` is parallel to the tangent at `A`. It intersects the line passing through `A` and `C` at `E`.

     


     
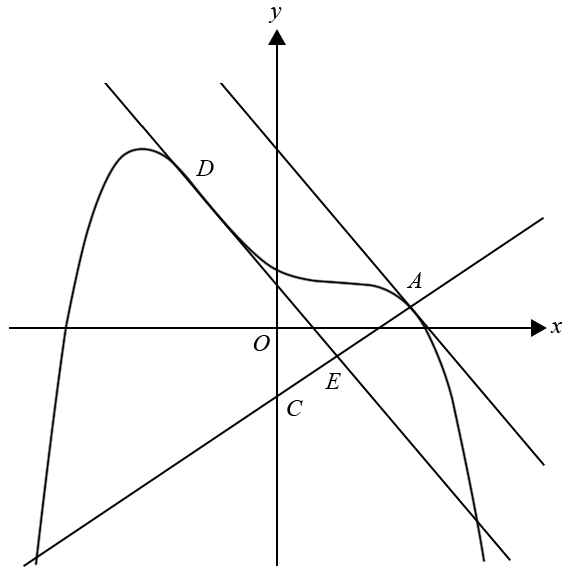
     i. Find the coordinates of `D`.  (2 marks)

  5. ii. Find the length of `AE`.  (3 marks)
Show Answers Only
  1.  i. `text(Proof)\ \ text{(See worked solutions)}`
  2. ii. `x = −2, 1`
  3.   i. `(0, 3)`
  4. ii. `y = 3/4 x-7/6`
  5.      `(0, −7/6)`
  6. iii. `25/6\ text(u²)`
  7. `(−1, 25/12)`
  8. `27/20\ text(u)`
Show Worked Solution
a.i.    `g(x)` `= int f(x)\ dx`
    `=-1/3 int (x + 2) (x-1)^2\ dx`
    `=-1/3int(x^3-3x+2)\ dx`
  `:.g(x)` `= -x^4/12 + x^2/2-(2x)/3 + c`

 

`text(S)text(ince)\ \ g(0) = 1,`

`1` `= 0 + 0-0 + c`
`:. c` `= 1`

 
`:. g(x) = -x^4/12 + x^2/2-(2x)/3 + 1\ \ …\ text(as required)`

 

a.ii.   `text(Stationary point when:)`

`g^{′}(x) = f(x) = 0`

`-1/3(x + 2) (x-1)^2=0`

`:. x = −2, 1`

 

b.i.   

`B\ text(is the)\ y text(-intercept of)\ \ y = 3-4/3 x`

`:. B (0, 3)`

 

b.ii.   `m_text(norm) = 3/4, \ text(passes through)\ \ A(2, 1/3)`

   `text(Equation of normal:)`

`y-1/3` `=3/4(x-2)`
`y` `=3/4 x -7/6`
   

`:. C (0, −7/6)`

 

b.iii.   `text(Area)` `= 1/2 xx text(base) xx text(height)`
    `= 1/2 xx (3 + 7/6) xx 2`
    `= 25/6\ text(u²)`

 

♦ Mean mark part (c)(i) 43%.
MARKER’S COMMENT: Many students gave an incorrect `y`-value here. Be careful!
c.i.    `text(Solve)\ \ \ g^{′}(x)` `= -4/3\ \ text(for)\ \ x < 0`
  `=> x` `= −1`
  `g(-1)` `=-1/12+1/2+2/3+1`
    `=25/12`

 
`:. D (−1, 25/12)`

 

c.ii.   `text(T) text(angent line at)\ \ D:`

`y-25/12` `=- 4/3(x+1)`
`y` `=- 4/3x + 3/4`

 

`DE\ \ text(intersects)\ \ AE\ text(at)\ E:`

♦♦ Mean mark 32%.
`-4/3 x + 3/4` `= 3/4 x-7/6`
`25/12 x` `= 23/12`
`x` `=23/25`

 
`:. E (23/25, -143/300)`

 

`:. AE` `= sqrt((2-23/25)^2 + (1/3-(-143/300))^2)`
  `= 27/20\ text(units)`

Graphs, MET2 2016 VCAA 6 MC

Consider the graph of the function defined by  `f: [0, 2 pi] -> R,\ f(x) = sin (2x).`

The square of the length of the line segment joining the points on the graph for which  `x = pi/4 and x = (3 pi)/4` is

  1. `(pi^2 + 16)/4`
  2. `pi + 4`
  3. `4`
  4. `(3 pi^2 + 16 pi)/4`
  5. `(10 pi^2)/16`
Show Answers Only

`A`

Show Worked Solution

`text(When)\ \ x=pi/4,\ \ f(x) = sin(pi/2)=1`

`text(When)\ \ x=(3pi)/4,\ \ f(x) = sin((3pi)/2)=-1`

`text(Let)\ \ z` `= text(distance between)\ (pi/4, 1) and ((3pi)/4, −1)`
`z^2` `= ((3pi)/4 – pi/4)^2 + (−1 −1)^2`
   `=pi^2/4 + 4`
  `= (pi^2 + 16)/4`

`=>   A`