v1 Measurement, STD2 M1 2017 HSC 22 MC
A concrete storm drain is constructed in the shape of a rectangular prism with a cylindrical tunnel running through its center. The dimensions are shown in the diagram.
What is the approximate volume of concrete needed to construct the storm drain?
- `text(4.5 m)³`
- `text(4.8 m)³`
- `text(5.1 m)³`
- `text(5.4 m)³`
v1 Measurement, STD2 M1 2009 HSC 19 MC
v1 Measurement, STD2 M1 2018 HSC 30a
v1 Measurement, STD2 M1 2021 HSC 16
The surface area, `A`, of a sphere is given by the formula
`A = 4 pi r^2,`
where `r` is the radius of the sphere.
A satellite dish resembles the inner surface of the lower half of a sphere with a radius of 1.5 meters.
Find the surface area of the satellite dish in square metres, correct to one decimal place. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
v1 Measurement, STD2 M1 2019 HSC 16
v1 Measurement, STD2 M1 SM-Bank 8
A cannonball is made out of lead and has a diameter of 18 cm.
- Find the volume of the sphere in cubic centimetres (correct to 1 decimal place). (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- It is known that the mass of lead is 11.3 tonnes/m³. Use this information to find the mass of the cannonball to the nearest gram. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2021 HSC 16
Measurement, STD2 M1 2019 HSC 16
Measurement, STD2 M1 2008 HSC 21 MC
A sphere and a closed cylinder have the same radius.
The height of the cylinder is four times the radius.
What is the ratio of the volume of the cylinder to the volume of the sphere?
- `2 : 1`
- `3 : 1`
- `4 : 1`
- `8 : 1`
Measurement, STD2 M1 2018 HSC 30a
Measurement, STD2 M1 2017 HSC 30e
A solid is made up of a sphere sitting partially inside a cone.
The sphere, centre `O`, has a radius of 4 cm and sits 2 cm inside the cone. The solid has a total height of 15 cm. The solid and its cross-section are shown.
Using the formula `V=1/3 pi r^2h` where `r` is the radius of the cone's circular base and `h` is the perpendicular height of the cone, find the volume of the cone, correct to the nearest cm³? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 SM-Bank 8
A cannon ball is made out of steel and has a diameter of 23 cm.
- Find the volume of the sphere in cubic centimetres (correct to 1 decimal place). (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- It is known that the mass of the steel used is 8.2 tonnes/m³. Use this information to find the mass of the cannon ball to the nearest gram. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2017 HSC 22 MC
Measurement, STD2 M1 2016 HSC 28e
A company makes large marshmallows. They are in the shape of a cylinder with diameter 5 cm and height 3 cm, as shown in the diagram.
- Find the volume of one of these large marshmallows, correct to one decimal place. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
A cake is to be made by stacking 24 of these large marshmallows and filling the gaps between them with chocolate. The diagrams show the cake and its top view. The shading shows the gaps to be filled with chocolate.
- What volume of chocolate will be required? Give your answer correct to the nearest whole number. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2005 HSC 28a
The Mitchell family has moved to a new house which has an empty swimming pool. The base of the pool is in the shape of a rectangle, with a semicircle on each end.
- Explain why the expression for the area of the base of the pool is `2xy + πy^2`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
The pool is 1.1 metres deep.
- The sides and base of the pool are covered in tiles. If `x =6` and `y = 2.5`, find the total area covered by tiles. (Give your answer correct to the nearest square metre.) (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
Before filling the pool, the Mitchells need to install a new shower head, which saves 6 litres of water per minute.
The shower is used 5 times every day, for 3 minutes each time.
- If the charge for water is $1.013 per kilolitre, how much money would be saved in one year by using this shower head? (Assume there are 365 days in a year.) (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2005 HSC 23b
A clay brick is made in the shape of a rectangular prism with dimensions as shown.
- Calculate the volume of the clay brick. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Three identical cylindrical holes are made through the brick as shown. Each hole has a radius of 1.4 cm.
- What is the volume of clay remaining in the brick after the holes have been made? (Give your answer to the nearest cubic centimetre.) (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- What percentage of clay is removed by making the holes through the brick? (Give your answer correct to one decimal place.) (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2007 HSC 23b
A cylindrical water tank, of height 2 m, is placed in the ground at a school.
The radius of the tank is 3.78 metres. The hole is 2 metres deep. When the tank is placed in the hole there is a gap of 1 metre all the way around the side of the tank.
- When digging the hole for the water tank, what volume of soil was removed? Give your answer to the nearest cubic metre. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- Sprinklers are used to water the school oval at a rate of 7500 litres per hour.
The water tank holds 90 000 litres when full.
For how many hours can the sprinklers be used before a full tank is emptied? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Water is to be collected in the tank from the roof of the school hall, which has an area of 400 m².
During a storm, 20 mm of rain falls on the roof and is collected in the tank.
How many litres of water were collected? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Measurement, STD2 M6 2008 HSC 25c
Pieces of cheese are cut from cylindrical blocks with dimensions as shown.
Twelve pieces are packed in a rectangular box. There are three rows with four pieces of cheese in each row. The curved surface is face down with the pieces touching as shown.
- What are the dimensions of the rectangular box? (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
- What is the volume of the remaining triangular prism of cheese? Answer to the nearest cubic centimetre. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2014 HSC 27c
Measurement, STD2 M1 2010 HSC 28b
Moivre’s manufacturing company produces cans of Magic Beans. The can has a diameter of 10 cm and a height of 10 cm.
- Cans are packed in boxes that are rectangular prisms with dimensions 30 cm × 40 cm × 60 cm.
What is the maximum number of cans that can be packed into one of these boxes? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- The shaded label on the can shown wraps all the way around the can with no overlap. What area of paper is needed to make the labels for all the cans in this box when the box is full? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- The company is considering producing larger cans. Monica says if you double the diameter of the can this will double the volume.
Is Monica correct? Justify your answer with suitable calculations. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
The company wants to produce a can with a volume of 1570 cm³, using the least amount of metal. Monica is given the job of determining the dimensions of the can to be produced. She considers the following graphs.
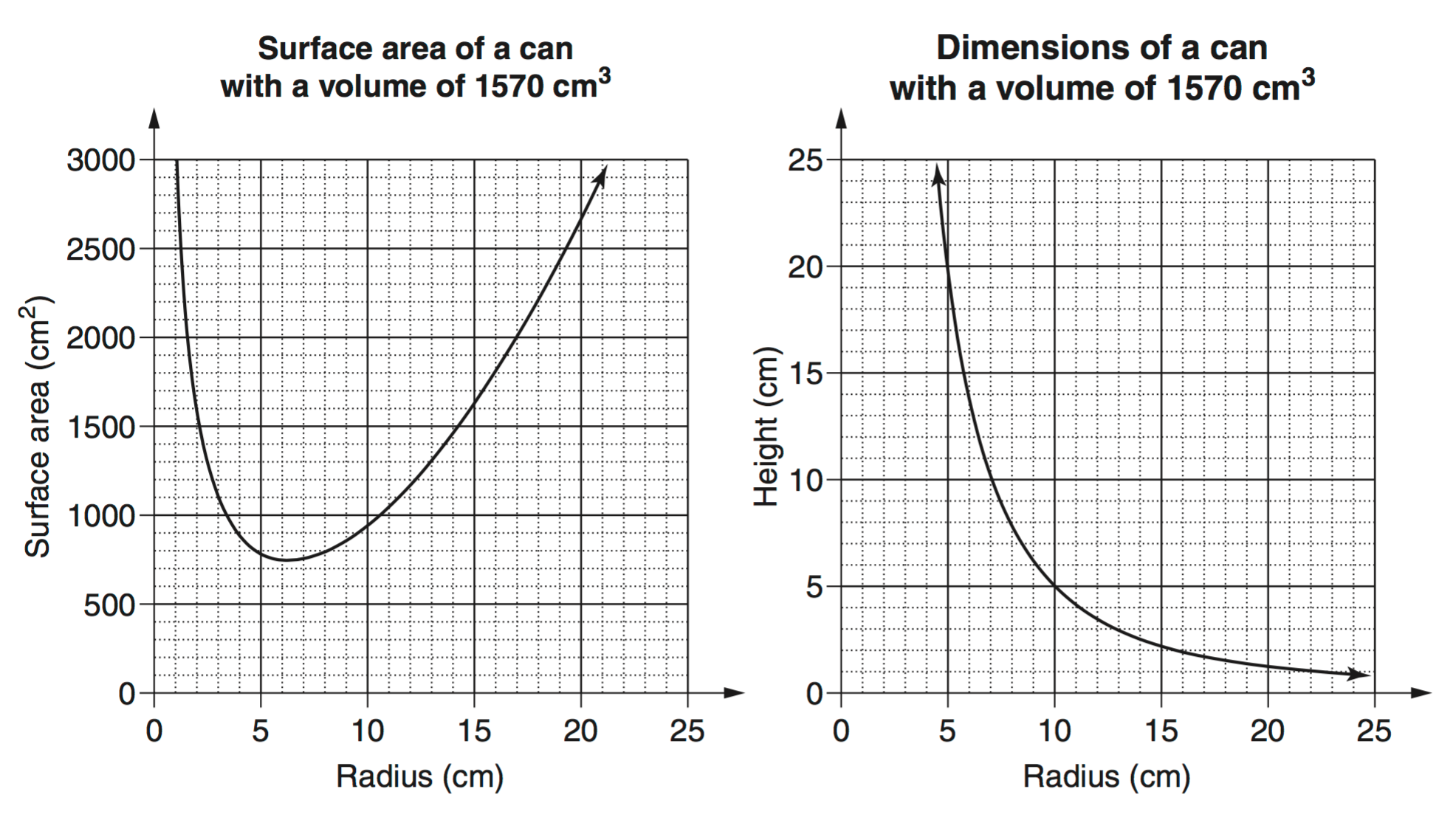
- What radius and height should Monica recommend that the company use to minimise the amount of metal required to produce these cans? Justify your choice of dimensions with reference to the graphs and/or suitable calculations. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---











