The diagram shows a triangle with sides of length `x` cm, 11 cm and 13 cm and an angle of 80°.
Use the cosine rule to calculate the value of `x`, correct to two significant figures. (3 marks)
Measurement, STD2 M6 2018 HSC 12 MC
The diagram shows a triangle with side lengths 8 m, 9 m and 10m.
What is the value of `theta`, marked on the diagram, to the nearest degree?
- 49°
- 51°
- 59°
- 72°
Measurement, STD2 M6 2015 HSC 30e
From point `S`, which is 1.8 m above the ground, a pulley at `P` is used to lift a flat object `F`. The lengths `SP` and `PF` are 5.4 m and 2.1 m respectively. The angle `PSC` is 108°.
- Show that the length `PC` is 6.197 m, correct to 3 decimal places. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Calculate `h`, the height of the object above the ground. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |
|
`text(Show)\ PC = 6.197\ text(m)`
♦ Mean mark 41%.
`text(Using the cosine rule in)\ Delta PSC`
| `PC^2` | `= PS^2 + SC^2-2 xx PS xx SC xx cos\ 108^@` |
| `= 5.4^2 + 1.8^2-2 xx 5.4 xx 1.8 xx cos\ 108^@` | |
| `= 38.4072…` | |
| `:.PC` | `= 6.19736…` |
| `= 6.197\ text{m (to 3 d.p.) …as required}` |
ii. `text(Let)\ \ SD⊥PE`
♦♦ Mean mark below 19%.
STRATEGY: Finding `PC` in part (i) and needing `PE` to find `h` should flag the strategy of finding `EC` and using Pythagoras.
STRATEGY: Finding `PC` in part (i) and needing `PE` to find `h` should flag the strategy of finding `EC` and using Pythagoras.
`∠DSC\ text(is a right angle)`
`:.∠DSP = 108^@-90^@ = 18^@`
`text(In)\ ΔPDS`
| `cos\ 18^@` | `= (DS)/5.4` |
| `DS` | `= 5.4 xx cos\ 18^@` |
| `= 5.1357…\ text(m)` |
`EC = DS = 5.1357…\ text{m (opposite sides of rectangle}\ DECS text{)}`
`text(Using Pythagoras in)\ Delta PEC:`
`PE^2 + EC^2 = PC^2`
| `PE^2 + 5.1357^2` | `= 6.197^2` |
| `PE^2` | `= 12.027…` |
| `PE` | `= 3.468…\ text(m)` |
`text(From the diagram,)`
| `h` | `= PE-PF` |
| `= 3.468…-2.1` | |
| `= 1.368…` | |
| `= 1.37\ text{m (to 2 d.p.)}` |
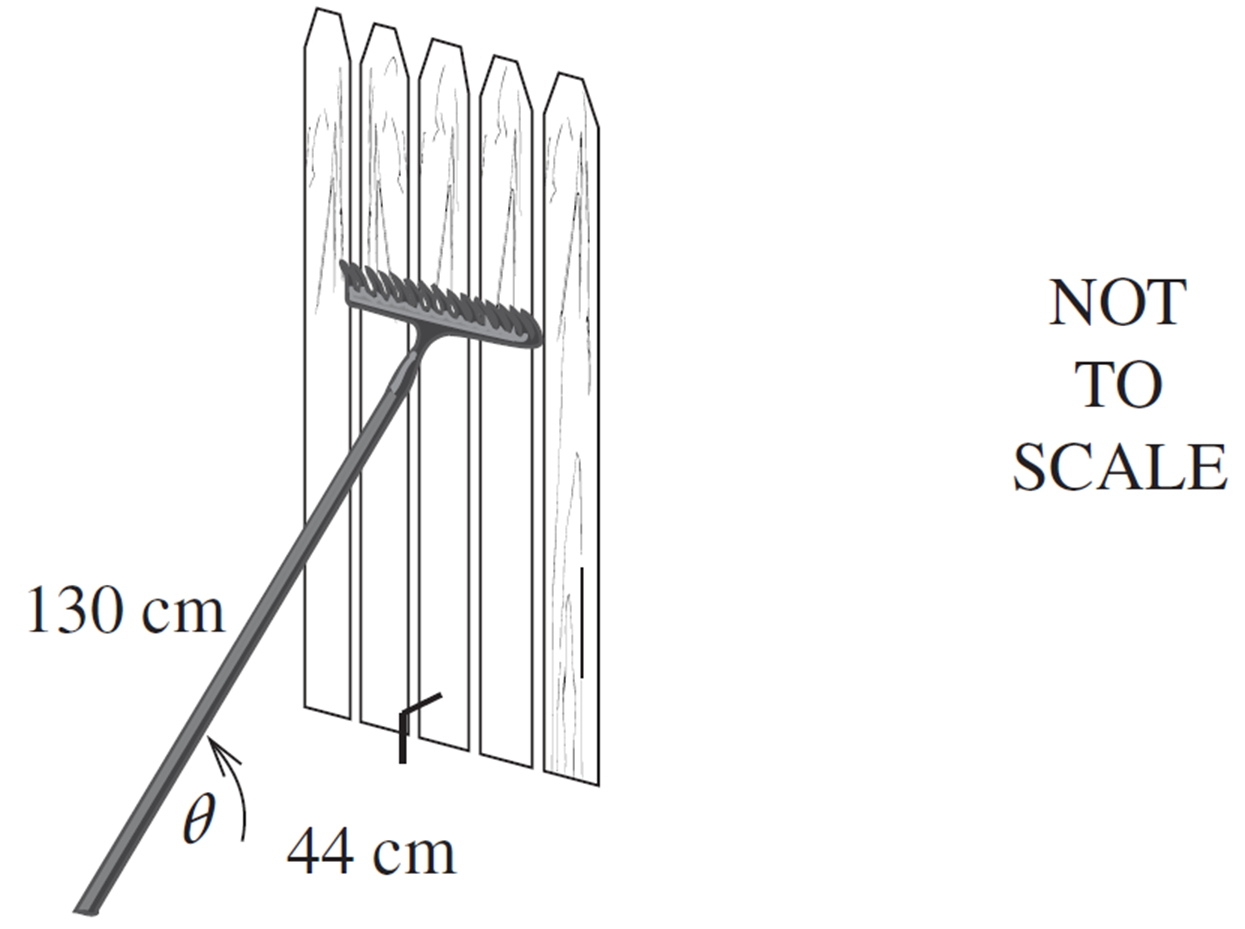
Measurement, STD2 M6 2006 HSC 24b
A 130 cm long garden rake leans against a fence. The end of the rake is 44 cm from the base of the fence.
- If the fence is vertical, find the value of `theta` to the nearest degree. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- The fence develops a lean and the rake is now at an angle of 53° to the ground. Calculate the new distance (`x` cm) from the base of the fence to the head of the rake. Give your answer to the nearest centimetre. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |
|
| `cos theta` | `= 44/130` |
| `= 70.216… ^@` | |
| `= 70^@\ \ \ text{(nearest degree)}` |
| ii. |
|
`text(Using cosine rule)`
| `x^2` | `= 130^2 + 44^2-2 xx 130 xx 44 xx cos 53^@` |
| `= 11\ 951.23…` | |
| `x` | `= 109.32…` |
| `= 109\ text{cm (nearest cm)}` |
Measurement, STD2 M6 2005 HSC 5 MC
Which formula should be used to calculate the distance between Toby and Frankie?
- `a/(sin A) = b/(sin B)`
- `c^2 = a^2 + b^2`
- `A = 1/2 ab\ sinC`
- `c^2 = a^2 + b^2 − 2ab\ cosC`
Measurement, STD2 M6 2008 HSC 25c
Pieces of cheese are cut from cylindrical blocks with dimensions as shown.
Twelve pieces are packed in a rectangular box. There are three rows with four pieces of cheese in each row. The curved surface is face down with the pieces touching as shown.
- What are the dimensions of the rectangular box? (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
To save packing space, the curved section is removed.
- What is the volume of the remaining triangular prism of cheese? Answer to the nearest cubic centimetre. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
i. `text(Box height) = 15\ text(cm)`
♦ Mean mark 45%.
`text{(radius of the arc)}`
| `text(Box width)` | `= 3 xx 7` |
| `= 21\ text(cm)` | |
| `text(Box length)` | `= 4x` |
`text(Using cosine rule)`
| `c^2` | `= a^2 + b^2 – 2ab cos C` |
| `x^2` | `= 15^2 + 15^2 – 2 xx 15 xx 15 xx cos 40^@` |
| `= 450 – 344.7199…` | |
| `= 105.2800…` | |
| `x` | `= 10.2606…` |
| `text(Box length)` | `= 4 xx 10.2606…` |
| `= 41.04…` |
`:.\ text(Dimensions are)\ \ 41\ text(cm) xx 21\ text(cm) xx 15\ text(cm)`
ii. `text(Volume) = Ah`
♦♦♦ Mean mark 22%.
`h = 7\ text(cm)`
`text(Find)\ A:`
| `A` | `= 1/2 ab sin C` |
| `= 1/2 xx 15 xx 15 xx sin 40^@` | |
| `= 72.3136…` |
| `:. V` | `= 72.3136… xx 7` |
| `= 506.195…` | |
| `= 506\ text(cm³)\ \ text{(nearest whole)}` |
Measurement, STD2 M6 2008 HSC 5 MC
Measurement, STD2 M6 2010 HSC 26d
Find the area of triangle `ABC`, correct to the nearest square metre. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Measurement, STD2 M6 2013 HSC 26a
Triangle `PQR` is shown.
Find the size of angle `Q`, to the nearest degree. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---