SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Measurement, STD2 M6 2024 HSC 36

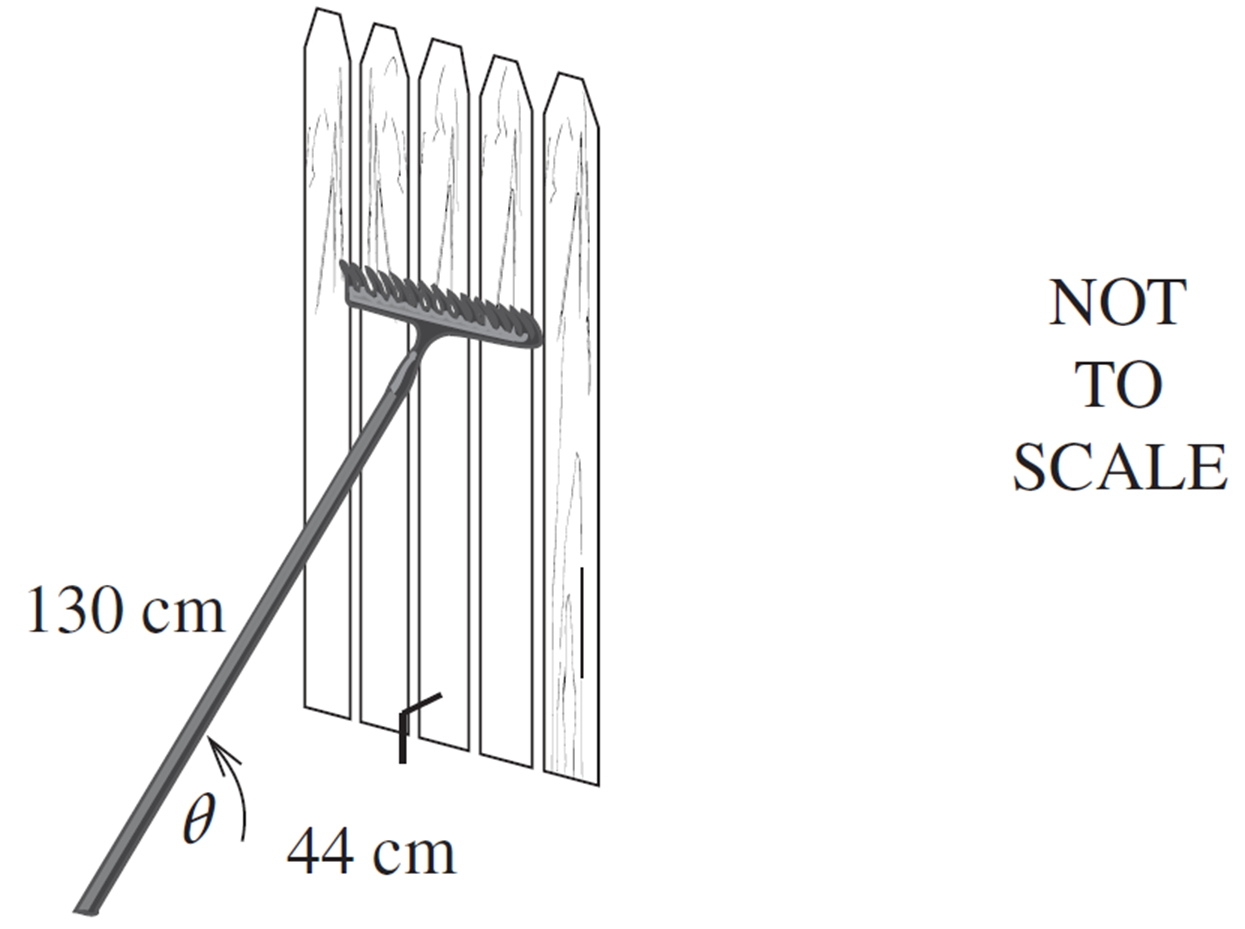
The diagram shows two vertical flagpoles, \(BE\) and \(CD\), set on sloping ground.
 

  1. What is the height of the flagpole \(BE\), correct to 1 decimal place?   (2 marks)
  2. What is the height of the flagpole \(CD\), correct to 1 decimal place?   (2 marks)
Show Answers Only

a.   \(BE=25.4\ \text{m}\)

b.   \(CD=19.7\ \text{m}\)

Show Worked Solution

a.   \(\text{Using the sine rule:}\)

\(\dfrac{BE}{\sin 27^{\circ}}\) \(=\dfrac{53.8}{\sin 106^{\circ}}\)  
\(\therefore BE\) \(=\dfrac{53.8 \times \sin 27^{\circ}}{\sin 106^{\circ}}\)  
  \(=25.408…\)  
  \(=25.4\ \text{m (1 d.p.)}\)  

 

b.   \(CD=EB-XB\)

\(\text{Consider}\ \Delta XBC:\)

\(\angle XBC=180-106=74^{\circ}, \ XC=ED=20\)

\(\tan 74^{\circ}\) \(=\dfrac{20}{XB}\)  
\(XB\) \(=\dfrac{20}{\tan 74^{\circ}}\)  
  \(=5.73\ \text{m}\)  

 
\(CD=25.4-5.73=19.7\ \text{m (1 d.p.)}\)

♦♦ Mean mark (b) 35%.

Measurement, STD2 M6 2022 HSC 26

The diagram shows two right-angled triangles, `ABC` and `ABD`,

where `AC=35 \ text{cm},BD=93 \ text{cm}, /_ACB=41^(@)` and `/_ADB=theta`.
 
     

Calculate the size of angle `theta`, to the nearest minute.  (4 marks)

Show Answers Only

`19^@6^{′}`

Show Worked Solution

`text{In}\ Delta ABC:`

`cos 41^@` `=35/(BC)`  
`BC` `=35/(cos 41^@)`  
  `=46.375…`  

 
`angle BCD = 180-41=139^@`
 

`text{Using sine rule in}\ Delta BCD:`

`sin theta/(46.375)` `=sin139^@/93`  
`sin theta` `=(sin 139^@ xx 46.375)/93`  
`:.theta` `=sin^(-1)((sin 139^@ xx 46.375)/93)`  
  `=19.09…`  
  `=19^@6^{′}\ \ text{(nearest minute)}`  

♦ Mean mark 50%.

Measurement, STD2 M6 2018 HSC 30c

The diagram shows two triangles.

Triangle `ABC` is right-angled, with  `AB = 13 text(cm)`  and  `/_ABC = 62°`.

In triangle  `ACD, \ AD = x\ text(cm)`  and  `/_DAC = 40°`. The area of triangle  `ACD`  is 30 cm².
 

 
What is the value of `x`, correct to one decimal place?  (3 marks)

Show Answers Only

`8.1\ text{cm  (1 d.p.)}`

Show Worked Solution

`text(Find)\ AC:`

♦ Mean mark 39%.

`sin62°` `= (AC)/13`
`AC` `= 13 xx sin62°`
  `= 11.478…`

 
`text(Using the sine rule in)\ DeltaACD :`

`text(Area)` `= 1/2 xx AC xx AD xx sin40°`
`30` `= 1/2 xx 11.478… xx x xx sin40°`
`:.x` `= (30 xx 2)/(11.478… xx sin40°)`
  `= 8.13…`
  `= 8.1\ text{cm  (1 d.p.)}`

Measurement, STD2 M6 2015 HSC 30e

From point `S`, which is 1.8 m above the ground, a pulley at `P` is used to lift a flat object `F`. The lengths `SP` and `PF` are 5.4 m and 2.1 m respectively. The angle `PSC` is 108°.
 

 

  1. Show that the length  `PC`  is 6.197 m, correct to 3 decimal places.  (1 mark)

  2. Calculate `h`, the height of the object above the ground.  (4 marks)

Show Answers Only
  1. `6.197\ text{m  (to 3 d.p.)  … as required}`
  2. `1.37\ text{m  (to 2 d.p.)}`
Show Worked Solution
i.   

2UG 2015 30e Answer

`text(Show)\ PC = 6.197\ text(m)`

♦ Mean mark 41%.

`text(Using the cosine rule in)\ Delta PSC` 

`PC^2` `= PS^2 + SC^2-2 xx PS xx SC xx cos\ 108^@`
  `= 5.4^2 + 1.8^2-2 xx 5.4 xx 1.8 xx cos\ 108^@`
  `= 38.4072…`
`:.PC` `= 6.19736…`
  `= 6.197\ text{m  (to 3 d.p.)  …as required}`

 

ii.   `text(Let)\ \ SD⊥PE`

♦♦ Mean mark below 19%.
STRATEGY: Finding `PC` in part (i) and needing `PE` to find `h` should flag the strategy of finding `EC` and using Pythagoras.

`∠DSC\ text(is a right angle)`

`:.∠DSP = 108^@-90^@ = 18^@`

 

`text(In)\ ΔPDS`

`cos\ 18^@` `= (DS)/5.4`
 `DS` `= 5.4 xx cos\ 18^@`
  `= 5.1357…\ text(m)`

 
`EC = DS = 5.1357…\ text{m  (opposite sides of rectangle}\ DECS text{)}`
 

`text(Using Pythagoras in)\ Delta PEC:`

`PE^2 + EC^2 = PC^2`

`PE^2 + 5.1357^2` `= 6.197^2`
`PE^2` `= 12.027…`
`PE` `= 3.468…\ text(m)`

 
`text(From the diagram,)`

`h` `= PE-PF`
  `= 3.468…-2.1`
  `= 1.368…`
  `= 1.37\ text{m  (to 2 d.p.)}`

Measurement, STD2 M6 2006 HSC 24b

A 130 cm long garden rake leans against a fence. The end of the rake is 44 cm from the base of the fence.

  1. If the fence is vertical, find the value of `theta` to the nearest degree.  (2 marks)
      
          2UG-2006-24b-i

     

  2. The fence develops a lean and the rake is now at an angle of 53° to the ground. Calculate the new distance (`x` cm) from the base of the fence to the head of the rake. Give your answer to the nearest centimetre.  (2 marks)
     
          2UG-2006-24b-ii

Show Answers Only
  1. `text{70°  (nearest degree)}`
  2. `text{109 cm  (nearest cm)}`
Show Worked Solution
i.   

2UG-2006-24b1 Answer
`cos theta` `= 44/130`
  `= 70.216… ^@`
  `= 70^@\ \ \ text{(nearest degree)}`

 

ii.   

2UG-2006-24b2 Answer

`text(Using cosine rule)`

`x^2` `= 130^2 + 44^2-2 xx 130 xx 44 xx cos 53^@`
  `= 11\ 951.23…`
`x` `= 109.32…`
  `= 109\ text{cm  (nearest cm)}`

Measurement, STD2 M6 2007 HSC 25b

The angle of depression from `J` to `M` is 75°. The length of `JK` is 20 m and the length of `MK` is 18 m.
 

 
 

Copy or trace this diagram into your writing booklet and calculate the angle of elevation from `M` to `K`. Give your answer to the nearest degree.   (3 marks)

Show Answers Only

`58^@`

Show Worked Solution

`/_AJL = 90^@`

`/_MJL = 90 – 75 = 15^@`

`text(Using sine rule in)\ Delta MJK`

`text(Let)\ /_JMK = x^@`

`20/sin x` `= 18/sin15^@`
`18 sin x` `= 20 xx sin 15^@`
`sin x` `= (20 xx sin 15^@)/18 = 0.2875…`
`x` `= 16.71…^@`
   
`/_JML = 75^@\ text{(} text(alternate angles,)\ ML \ text(||) \ AJ text{)}`

 

`:.\ /_KML` `= 75^@ – 16.71…`
  `= 58.287…^@`
  `= 58^@\ \ \ text{(nearest degree)}`

 

`:.\ text(Angle of Elevation from)\ M\ text(to)\ K\ text(is)\ 58^@.`

Measurement, STD2 M6 2010 HSC 24d

The base of a lighthouse, `D`, is at the top of a cliff 168 metres above sea level. The angle of depression from `D` to a boat at `C` is 28°. The boat heads towards the base of the cliff, `A`, and stops at `B`. The distance `AB` is 126 metres.
 

  1. What is the angle of depression from `D` to `B`, correct to the nearest degree?   (3 marks)

  2. How far did the boat travel from `C` to `B`, correct to the nearest metre?   (2 marks)

Show Answers Only
  1. `53^circ`
  2. `190\ text(m)`
Show Worked Solution
♦♦ Mean mark 31%
i.    `tan/_ADB` `=126/168`
  ` /_ADB` `=36.8698…`
    `=36.9^circ\ \ \ \ text{(to 1 d.p)}` 

 

`/_text(Depression)\ D\ text(to)\ B` `=90-36.9`
  `=53.1`
  `=53^circ\ text{(nearest degree)}`

 

ii.     `text(Find)\ CB:`

♦♦ Mean mark 31%
MARKER’S COMMENT: Solve efficiently by using right-angled trigonometry. Many students used non-right angled trig, adding to the calculations and the difficulty.
`/_ADC+28` `=90`
 `/_ADC` `=62^circ`
`tan 62^circ` `=(AC)/168`
`AC` `=168xxtan 62^circ`
  `=315.962…`

 

`CB` `=AC-AB`
  `=315.962…-126`
  `=189.962…`
  `=190\ text(m (nearest m))`

Measurement, STD2 M6 2009 HSC 22 MC

In the diagram, `AD` and `DC` are equal to 30 cm. 
 

2UG-2009-22MC
 

 What is the length of `AB` to the nearest centimetre? 

  1.    `28\ text(cm)`
  2.    `31\ text(cm)` 
  3.    `34\ text(cm)`
  4.    `39\ text(cm)` 
Show Answers Only

`A`

Show Worked Solution
♦ Mean mark of 35%

`Delta ADC\ text(is isosceles)`

`/_DAB = /_DCA` `= x^@`
`2x + 80^@` `= 180^@\ \ \ (text{Angle sum of}\ DeltaADC)`
`2x` `= 100^@`
`x` `= 50^@`

 

`/_ DBA` `= 180\-(50 + 60)\ \ \ (text{Angle sum of}\ Delta ADB)`
  `= 70^@`

 

`text(Using sine rule:)`

`(AB)/sin60` `= 30/sin70`
`AB` `= (30 xx sin60)/sin70`
  `= 27.648…\ text(cm)`

`=>  A`

Measurement, STD2 M6 2012 HSC 29c

Raj cycles around a course. The course starts at `E`, passes through `F`, `G` and `H` and finishes at `E`. The distances `EH` and `GH` are equal.
  

2012 29c

  1. What is the length of `EF`, to the nearest kilometre?  (2 marks)

  2. What is the total distance that Raj cycles, to the nearest kilometre?   (3 marks)

Show Answers Only
  1. `22\ text{km    (nearest km)}`
  2. `202\ text{km    (nearest km)}`
Show Worked Solution

i.   `text(Find)\ EF:`

♦ Mean mark 48%.
`/_ FGE` `= 180\-(139 + 31) \ \ text{(angle sum of}\ Delta EFGtext{)}`
  `= 180-170`
  `= 10^@`

 
`text(Using Sine rule:)`

`(EF)/sin10^@` `= 82/sin139^@`
`EF` `= (82 xx sin10^@)/sin139^@`
  `= 21.70406…`
  `= 22\  text{km (nearest km)}`

 

ii.  `text(Let)\ \ d = text(total distance cycled)`

`text(Find)\ EH`

`text(S)text(ince)\ Delta EGH\ text(is isosceles, and)\ /_EHG = 90^@`

`/_GEH = /_HGE = 45^@`

`text{(angles opposite equal sides in}\ Delta EGHtext{)}`

♦ Mean mark 37%.
MARKER’S COMMENT: Students could also have used Pythagoras or the Sine rule to calculate `GH`.
`sin45^@` `= (GH)/82`
`GH` `= 82 xx sin45^@`
  `= 57.983…`

 

`:. d` `= EF + FG + GH + EH`
  `= 21.704… + 64 + 57.983 + 57.983`
  `= 201.66…`
  `= 202 \ text{km (nearest km)}`

Measurement, STD2 M6 2013 HSC 24 MC

What is the value of  `theta`,  to the nearest degree?

2013 24 mc

  1.    `21^@`
  2.    `32^@`
  3.    `43^@`
  4.    `55^@`
Show Answers Only

`C`

Show Worked Solution
`a/sinA` `=b/sinB`
`82/sinA` `=100/sin26`
`sin A` `=(82 xx sin26)/100`
  `=0.35946…`
`/_A` `=21^@\ \ \ \ text{(nearest degree)}`

 
`text(S)text(ince)\   180^@\ text(in)\ Delta:`

`90+26+(theta+21)` `=180`
`theta` `=43^@`

 
`=>  C`