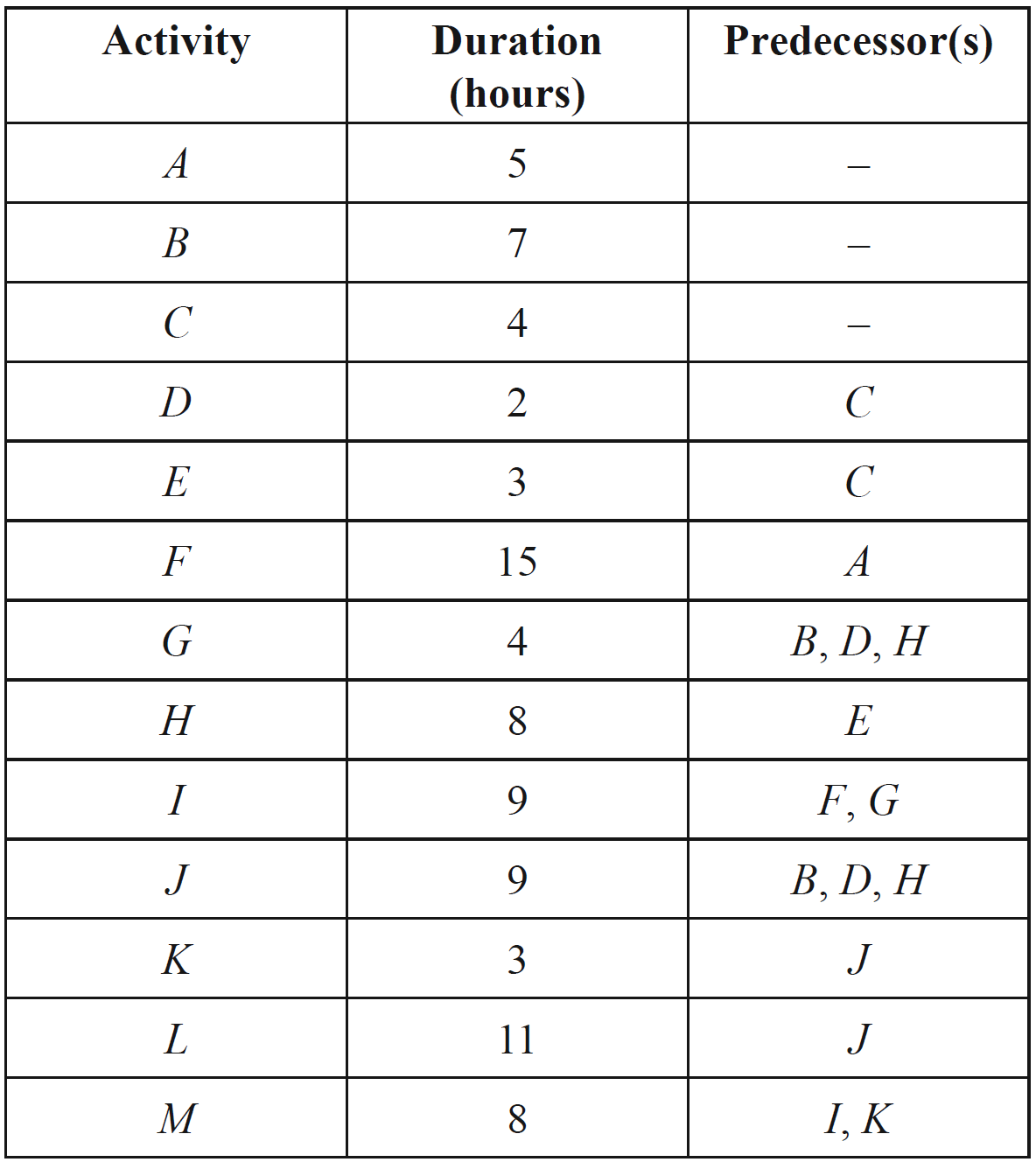
The activities and corresponding durations in days for a project are shown in the network diagram.
- Complete the table showing the immediate prerequisites for each activity. Indicate with an \(\text{X}\) any activities without any immediate prerequisites. (2 marks)
\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \text{Activity} \rule[-1ex]{0pt}{0pt} & \text{Immediate prerequisite(s)} \\
\hline
\rule{0pt}{2.5ex} B \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} E \rule[-1ex]{0pt}{0pt} & \\
\hline
\rule{0pt}{2.5ex} F \rule[-1ex]{0pt}{0pt} & \\
\hline
\end{array}
- Find the critical path for this project AND state the minimum duration for the project. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
-
The duration of activity \( A \) is increased by 2. Does this affect the critical path for the project? Give a reason for your answer. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---