SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, STD2 N3 2023 HSC 31

A function centre employs staff so that all necessary tasks can be completed between the end of one function and the beginning of the next function.

The network diagram shows the time taken in hours for the tasks that need to be completed.
 


 

  1. Find the TWO critical paths.  (2 marks)

  2. The function centre wants to decrease the length of each critical path by 3 hours. They can do this by hiring more staff to do ONE of the tasks so it takes less time to complete.
  3. For which task should the centre hire more staff, and how long should that task take to ensure all tasks can be completed in 14 hours?  (2 marks) 

Show Answers Only

a.    `HIGC and HIK`

b.    `text{More staff should be hired for task}\ I.`

`text{By decreasing task}\ I\ text{by 3 hours (so it takes 4 hours), the}`

`text{critical path of the network reduces to 14 hours.}`

Show Worked Solution

a.    `text{Scanning both ways:}`
 

`text{Critical paths:}\ HIGC and HIK`

♦ Mean mark (a) 46%.

 
b.   `text{More staff should be hired for task}\ I.`

`text{By decreasing task}\ I\ text{by 3 hours (so it takes 4 hours), the}`

`text{critical path of the network reduces to 14 hours.}`

Mean mark (b) 52%.

Networks, STD2 N3 SM-Bank 50

Roadworks planned by the local council require 13 activities to be completed.

The network below shows these 13 activities and their completion times in weeks.
 

  1. What is the earliest start time, in weeks, of activity `K`?  (1 mark)

  2. How many of these activities have zero float time?  (2 marks)

  3. It is possible to reduce the completion time for activities `A, E, F, L` and `K`.
  4. The reduction in completion time for each of these five activities will incur an additional cost.
  5. The table below shows the five activities that can have their completion time reduced and the associated weekly cost, in dollars.
     
       
  6. The completion time for each these five activities can be reduced by a maximum of two weeks.
  7. The overall completion time for the roadworks can be reduced to 16 weeks.
  8. What is the minimum cost, in dollars, of this change in completion time?  (3 marks)

Show Answers Only
  1. `14 \ text{weeks}`
  2. `7`
  3. `$ 380 \ 000`
Show Worked Solution

a.    `text{Scan forwards:}`

`EST \ (text{activity} \ K)`

`= A \ E \ J`

`= 6 + 5 + 3`

`= 14 \ text{weeks}`
 

b.     `text{Scan backwards:}`

`text{Critical paths:}\ ADGLM\ text(and)\ AEHLM`

`:. \ text{7 activities have no float time:} \ ADEGHLM`
 

c.    `text{There are 9 possible paths}`

`ADGLM\ (19), AEHLM\ (19) , AEIM\ (14)`

`AEJK\ (17), BCEIM \ (13), BCEJK\ (16)`

`BCEHLM\ (18), BCDGLM \ (18), BFK (11)`

`text{Consider the 5 paths with completions over 16 weeks}`

` to \ text{all contain}\ A\ text{or}\ L \ text{or both.}`
  

`text{Consider} \ ADGLM, AEHLM \ (text{contains both} \ A\ text{and} \ L )`

`to \ text{reduce} \ L xx 2 \ ,  A xx 1 \ text{to reach 16 weeks}`

`to \ text{cheaper than} \ L xx 1 \ , \ A xx 2`
  

`text{Consider} \ BCEHLM , BCDGLM\ (text{both contain} \ L \ text{only})`

`to \ text{reduce} \ L xx 2 \ text{to reach 16 weeks}`
 

`text{Consider} \ AEJK \ ( text{contains} \ A \ text{only} )`

`to \ text{reduce} \ A xx 1 \ text{reach 16 weeks}.`
 

`:. \ text{Minimum cost to reduce time to 16 weeks}`

`= 2 xx 120\ 000 + 1 xx  140\ 000`

`= $ 380\ 000`

Networks, STD2 N3 2021 FUR1 6

The directed graph below shows the sequence of activities required to complete a project.

The time taken to complete each activity, in hours, is also shown.
 

The minimum completion time for this project is 18 hours.

The time taken to complete activity `E` is labelled  `x`.

What is the maximum value of  `x`?   (2 marks)

Show Answers Only

`text(3 hours)`

Show Worked Solution

`text{Consider all possible network paths:}`

`ADHJ \ -> \ text{18 hours}`

`BEJ \ -> \ (12 + x) \ text{hours}`

`CGFEJ \ -> \  (15 + x) \ text{hours}`

`CGIJ \ -> \ text{18 hours}`
 

`text{Minimum completion time = 18 hours}`

`=>\ text{No path can be longer than 18 hours}`

`:. \ x_text{max} = 3 \ text{hours}`

Networks, STD2 N3 2019 FUR2 3

Fencedale High School is planning to renovate its gymnasium.

This project involves 12 activities, `A` to `L`.

The directed network below shows these activities and their completion times, in weeks.
 


 

The minimum completion time for the project is 35 weeks.

  1. Identify the critical path and state how many activities are on it?  (2 marks)

  2. Determine the latest start time of activity `E`.  (1 mark)

  3. Which activity has the longest float time?  (1 mark)

It is possible to reduce the completion time for activities `C, D, G, H` and `K` by employing more workers.

  1.  The completion time for each of these five activities can be reduced by a maximum of two weeks.

      

    What is the minimum time, in weeks, that the renovation project could take?  (1 mark)

Show Answers Only
  1. `8\ text(activities)`
  2. `12\ text(weeks)`
  3. `text(Activity)\ J`
  4. `29\ text(weeks)`
Show Worked Solution

a.  `text(Scanning forwards and backwards:)`
 

 

 

`text(Critical path:)\ ABDFGIKL`

`:. 8\ text(activities)`
 

b.  `text(LST for activity)\ E = 12\ text{weeks  (i.e. start of 13th week)}`
 

c.   `text(Consider float times of all activities not on critical path.)`

`J-5, H-1, E-1, C-1`

`:.\ text(Activity)\ J\ text(has the largest float time.)`
 

d.   `text(Critical path after reducing)\ CDGHK\ text(by 2 weeks is)`

`ABDFGIKL.`
 

`:.\ text(Minimum time)` `= 2 + 4 + 7 + 1 + 2 + 2 + 5 + 6`
  `= 29\ text(weeks)`

Networks, STD2 N3 2013 FUR2 2

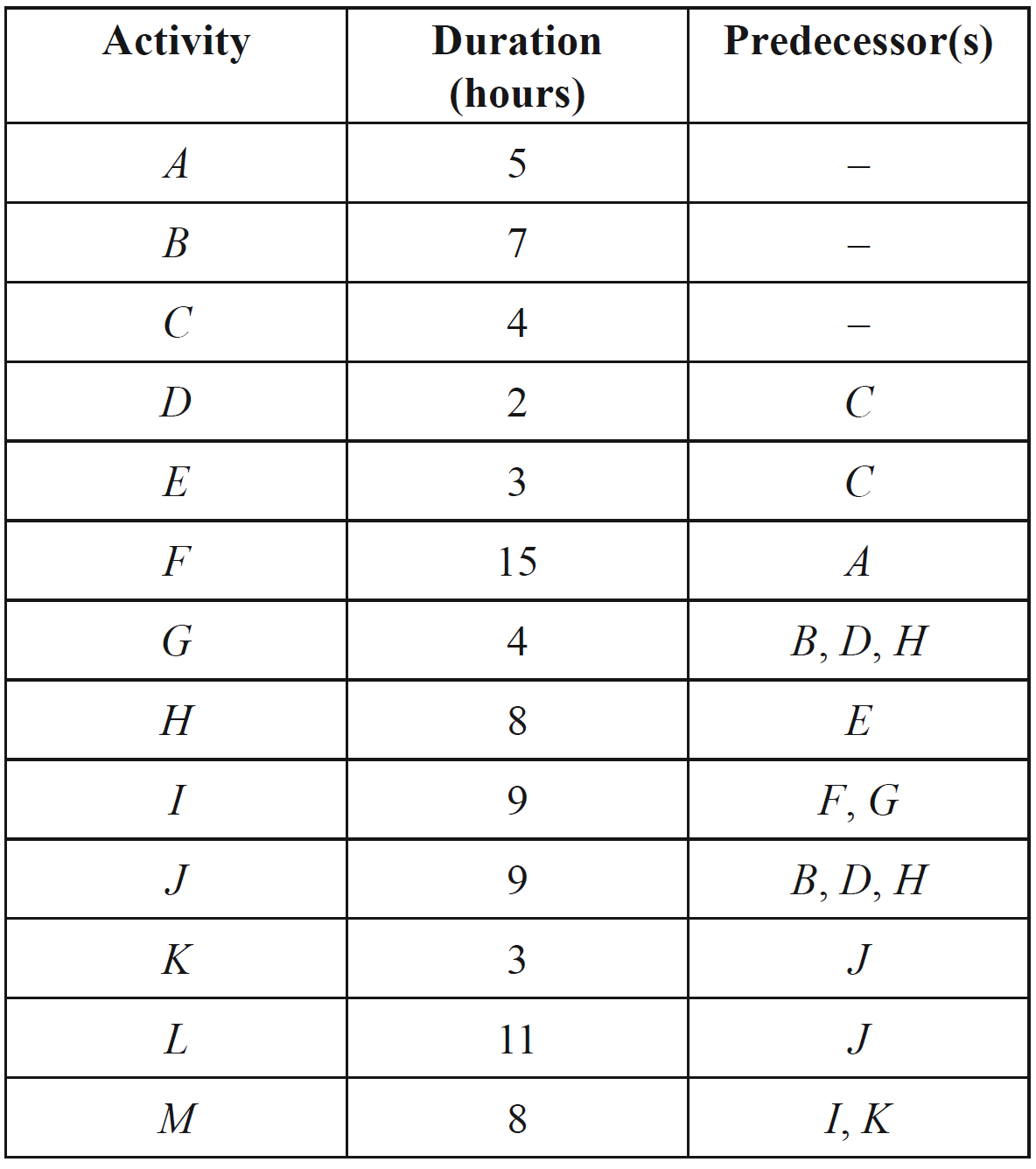
A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.


NETWORKS, FUR2 2013 VCAA 21
 

Activity `G` is missing from the network diagram for this project, which is shown below.

 
NETWORKS, FUR2 2013 VCAA 22
 

  1. Complete the network diagram above by inserting activity `G`.  (1 mark)
  2. Determine the earliest starting time of activity `H`.  (1 mark)

  3. Given that activity `G` is not on the critical path

     

    1. write down the activities that are on the critical path in the order that they are completed  (1 mark)

    2. find the latest starting time for activity `D`.  (1 mark)

  4. Consider the following statement.

     

    ‘If the time to complete just one of the activities in this project is reduced by one hour, then the minimum time to complete the entire project will be reduced by one hour.’

    Explain the circumstances under which this statement will be true for this project.  (1 mark)

  5. Assume activity `F` is reduced by two hours.
    What will be the minimum completion time for the project?  (1 mark)

Show Answers Only

a.

networks-fur2-2013-vcaa-2-answer

b.  `7\ text(hours)`

c.i.  `AFIM`

c.ii. `14\ text(hours)`

d.  `text(The statement will only be true if the crashed activity)`
      `text(is on the critical path)\ \ A F I M.`

e.  `text(36 hours)`

Show Worked Solution
a.    networks-fur2-2013-vcaa-2-answer

 

b.  `text(Scanning forwards and backwards:)`

`text(EST for Activity)\ H`

`= 4 + 3`

`= 7\ text(hours)`
 

c.i.   `A F I M`

♦♦ Mean mark of parts (c)-(e) (combined) was 40%.
 

c.ii.  `text(LST of)\ G = 20 – 4 = 16\ text(hours)`

 `text(LST of)\ D = 16 – 2 = 14\ text(hours)`
 

d.   `text(The statement will only be true if the time reduced activity)`

MARKER’S COMMENT: Most students struggled with part (d).

`text(is on the critical path)\ \ A F I M.`
 

e.   `A F I M\ text(is 37 hours.)`

`text(If)\ F\ text(is reduced by 2 hours, the new critical)`

`text(path is)\ \ C E H G I M\ text{(36 hours)}`

`:.\ text(Minimum completion time = 36 hours)`

Networks, STD2 N3 2009 FUR2 4

A walkway is to be built across the lake.

Eleven activities must be completed for this building project.

The directed network below shows the activities and their completion times in weeks.
 

NETWORKS, FUR2 2009 VCAA 4
 

  1. What is the earliest start time for activity E?  (1 mark)

  2. Write down the critical path for this project.  (1 mark)

  3. The project supervisor correctly writes down the float time for each activity that can be delayed and makes a list of these times.

     

    Determine the longest float time, in weeks, on the supervisor’s list.  (1 mark)

A twelfth activity, L, with duration three weeks, is to be added without altering the critical path.

Activity L has an earliest start time of four weeks and a latest start time of five weeks.
 

NETWORKS, FUR2 2009 VCAA 4
 

  1. Draw in activity L on the network diagram above.  (1 mark)
  2. Activity L starts, but then takes four weeks longer than originally planned.

     

    Determine the total overall time, in weeks, for the completion of this building project.  (1 mark)

Show Answers Only
  1. `7`
  2. `BDFGIK`
  3. `H\ text(or)\ J\ text(can be delayed for)`
    `text(a maximum of 3 weeks.)`
  4.  
    NETWORKS, FUR2 2009 VCAA 4 Answer
  5. `text(25 weeks)`
Show Worked Solution

a.   `7\ text(weeks)`

♦ Mean mark of all parts (combined): 44%.

 

b.  `text(Scanning forwards and backwards)`
 

 
`text(Critical Path is)\ BDFGIK`

 

c.   `H\ text(or)\ J\ text(can be delayed for a maximum)`

`text(of 3 weeks.)`
 

d.    NETWORKS, FUR2 2009 VCAA 4 Answer

 

e.   `text(The new critical path is)\ BLEGIK.`

`=>\ text(Activity)\ L\ text(now takes 7 weeks.)`

`:.\ text(Time for completion)`

`= 4 + 7 + 1 + 5 + 2 + 6`

`= 25\ text(weeks)`

Networks, STD2 N3 2014 FUR1 8 MC

Which one of the following statements about critical paths is true?

  1. There can be only one critical path in a project.
  2. A critical path will always include the activity that takes the longest time to complete.
  3. Reducing the time of any activity on a critical path for a project will always reduce the minimum completion time for the project.
  4. If there are no other changes, increasing the time of any activity on a critical path will always increase the completion time of a project.
Show Answers Only

`D`

Show Worked Solution

`text(If any activity on a critical path takes longer, the project)`

♦ Mean mark 40%.

`text{completion time increases by the equivalent amount}`

`text{of time (although the reverse is not true).}`

`=>  D` 

Networks, STD2 N3 SM-Bank 47

The directed graph below shows the sequence of activities required to complete a project.

All times are in hours.
 


 

  1.  Find the number of activities that have exactly two immediate predecessors. (1 mark)

  2. Identify the critical path for this project. (3 marks)
  3. If Activity E is reduced by one hour, identify the two new critical paths. (1 mark)

Show Answers Only
  1. `2`
  2. `BEIL`
  3. `ADIL and CHKL`
Show Worked Solution

i.    `I\ text(and)\ J`

`:.\ text(2 activities have exactly two immediate predecessors.)`

 

ii.   `text(Scanning forwards:)`
 


 

`:.\ text(Initial critical path)\ BEIL`

 

iii.   `text(If)\ E\ text(reduced by 1 hour, critical path)\ BEIL`

`text(reduces to 19 hours.)`

`:.\ text(Other critical paths of 19 hours are:)`

`ADIL = 5 + 2 + 4 + 8 = 19`

`CHKL = 2 + 6 + 3 + 8 = 19`

Networks, STD2 N3 2008 FUR1 8-9 MC

The network below shows the activities that are needed to finish a particular project and their completion times (in days).
 

networks-fur1-2008-vcaa-8-mc

 
Part 1

The earliest start time for Activity K, in days, is

A.     `7`

B.   `15`

C.   `16`

D.   `19`

 

Part 2

This project currently has one critical path.

A second critical path, in addition to the first, would be created by

A.   increasing the completion time of D by 7 days.

B.   increasing the completion time of G by 1 day.

C.   increasing the completion time of I by 2 days.

D.   decreasing the completion time of C by 1 day.

Show Answers Only

`text(Part 1:)\ C`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

`text(Scanning forwards:)`
 

 
`text(EST for Activity)\ K`

`=\ text(Duration)\ ACFI`

`= 2 + 5 + 6 + 3`

`= 16`

`=> C`

 

`text(Part 2)`

♦♦ Mean mark of Part 2 was 35%.

`text(Original critical path:)\ ACFHJL\ text{(22 days)}`
 

`text(Consider option)\ A,`

`text(New critical path:)\ ABDJL\ text{(22 days)}`

`=> A`