The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.
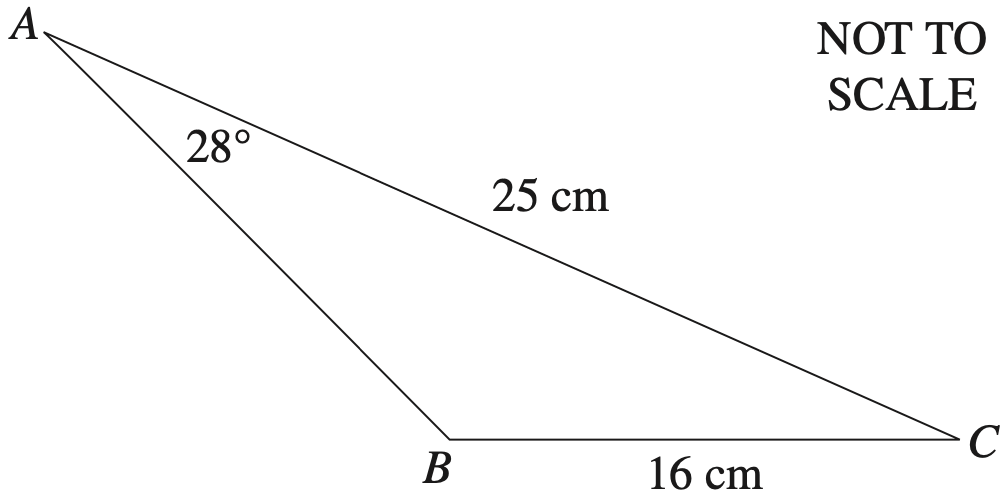
Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Aussie Maths & Science Teachers: Save your time with SmarterEd
The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.

Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`133°`
`text(Using the sine rule:)`
| `sin theta/25` | `= (sin 28°)/16` |
| `sin theta` | `= (25 xx sin 28°)/16` |
| `sin theta` | `= 0.73355` |
| `theta` | `= 47°` |
Determine all possible dimensions for triangle `ABC` given `AB = 6.2\ text(cm)`, `angleABC = 35°` and `AC = 4.1`.
Give all dimensions correct to one decimal place. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
`text(7.1 cm, 6.2 cm, 4.1 cm or)`
`text(3.0 cm, 6.2 cm, 4.1 cm.)`
`text(Using the sine rule:)`
| `(sinangleACB)/6.2` | `= (sin35^@)/4.1` |
| `sinangleACB` | `= (6.2 xx sin35^@)/4.1` |
| `= 0.8673…` | |
| `angleACB` | `= 60.15…^@\ text(or)\ 119.84…^@` |
`text(If)\ \ angleACB = 60.15^@,`
`angleBAC = 180-(35 + 60.15) = 84.85^@`
| `(BC)/(sin84.85)` | `= 4.1/(sin35^@)` |
| `BC` | `= 7.11… = 7.1\ text(cm)` |
`text(If)\ \ angleACB = 119.85^@,`
`angleBAC = 180-(35 + 119.85) = 25.15^@`
| `(BC)/(sin25.15)` | `= 4.1/(sin35^@)` |
| `BC` | `= 3.03… = 3.0\ text(cm)` |
`:.\ text(Possible dimensions are:)`
`text(7.1 cm, 6.2 cm, 4.1 cm or)`
`text(3.0 cm, 6.2 cm, 4.1 cm.)`
The diagram shows a circle with centre `O` and radius 2 centimetres. The points `A` and `B` lie on the circumference of the circle and `/_AOB = theta`.
Find the other value. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
(1) Find the area of sector `AOB` (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
(2) Find the exact length of the perimeter of the minor segment bounded by the chord `AB` and the arc `AB`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
| i. | `text(Area)\ Delta AOB` | `= 1/2 ab sin theta` |
| `= 1/2 xx 2 xx 2 xx sin theta` | ||
| `= 2 sin theta` |
| `2 sin theta` | `= sqrt 3\ \ \ text{(given)}` |
| `sin theta` | `= sqrt3/2` |
| `:. theta` | `= pi/3,\ pi-pi/3` |
| `= pi/3,\ (2pi)/3` |
`:.\ text(The other value of)\ theta\ text(is)\ \ (2pi)/3\ \ text(radians)`
| ii.(1) | `text(Area of sector)\ AOB` | `= pi r^2 xx theta/(2pi)` |
| `= 1/2 r^2 theta` | ||
| `= 1/2 xx 2^2 xx pi/3` | ||
| `= (2pi)/3\ text(cm²)` |
| ii.(2) | `text(Using the cosine rule:)` |
| `AB^2` | `= OA^2 + OB^2-2 xx OA xx OB xx cos theta` |
| `= 2^2 + 2^2-2 xx 2 xx 2 xx cos (pi/3)` | |
| `= 4 + 4-4` | |
| `= 4` | |
| `:.\ AB` | `= 2` |
| `text(Arc)\ AB` | `= 2 pi r xx theta/(2pi)` |
| `= r theta` | |
| `= (2pi)/3\ text(cm)` |
`:.\ text(Perimeter) = (2 + (2pi)/3)\ text(cm)`