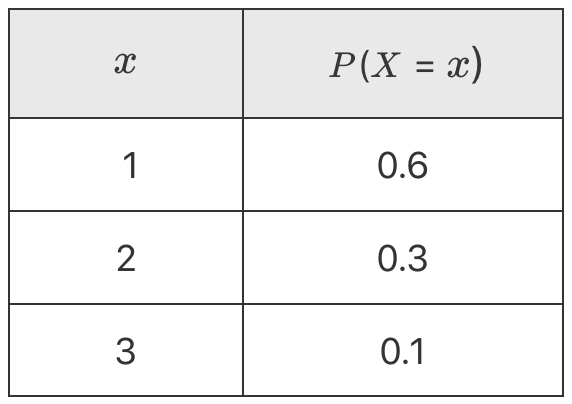
The table shows the probability distribution of a discrete random variable.
\begin{array} {|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} x \rule[-1ex]{0pt}{0pt} & 0 & 1 & 2 & 3 & 4 \\
\hline
\rule{0pt}{2.5ex} P(X = x) \rule[-1ex]{0pt}{0pt} & \ \ \ 0\ \ \ & \ \ 0.3\ \ & \ \ 0.5\ \ & \ \ 0.1\ \ & \ \ 0.1\ \ \\
\hline
\end{array}
- Show that the expected value `E(X)=2`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Calculate the standard deviation, correct to one decimal place. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---