Special Properties

Special Properties, SMB-031

In the diagram, `ABCDE` is a regular pentagon. The diagonals `AC` and `BD` intersect at `F`.

Show that the size of `/_ABC` is 108°. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Find the size of `/_BAC`. Give reasons for your answer. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solutions)`
`36°`

Show Worked Solution

`text(Sum of all internal angles)`

`= (n-2) xx 180°`

`= (5-2) xx 180°`

`= 540°`

`:. /_ABC= 540/5= 108°`

ii. `BA = BC\ \ text{(equal sides of a regular pentagon)}`

`:. Delta BAC\ text(is isosceles)`

`/_BAC= 1/2 (180-108)=36^{\circ} \ \ \ text{(base angle of}\ Delta BAC text{)}`

Special Properties, SMB-025

A quadrilateral is pictured below.

What is the value of `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`126^@`

Show Worked Solution

`text{Sum of exterior angles = 360°}`

`y^{\circ}`	`=360-(127+114+65)`
	`=360-306`
	`=54^{\circ}`

`:.x^{\circ}=180-54 = 126^{\circ}\ \ \text{(180° in straight line)}`

Special Properties, SMB-026

A pentagon is pictured below, where one internal angle is a right angle.

What is the value of `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`130^@`

Show Worked Solution

`y^{\circ}=180-100 = 80^{\circ}\ \ \text{(180° in straight line)}`

`text{Sum of exterior angles = 360°}`

`z^{\circ}`	`=360-(70+70+90+80)`
	`=360-310`
	`=50^{\circ}`

`:.x^{\circ}=180-50 = 130^{\circ}\ \ \text{(180° in straight line)}`

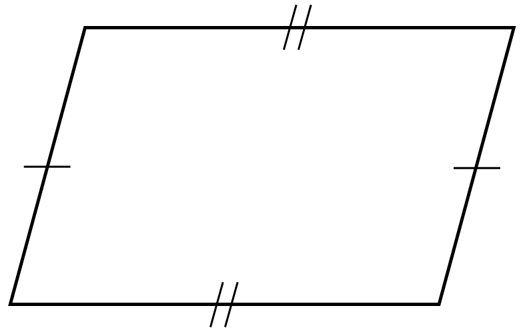
Special Properties, SMB-024

A quadrilateral is drawn below.

What is the value of `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`117^@`

Show Worked Solution

`y^{\circ}=180-75 = 105^{\circ}\ \ \text{(180° in straight line)}`

`text{Sum of exterior angles = 360°}`

`z^{\circ}`	`=360-(130+105+62)`
	`=360-297`
	`=63^{\circ}`

`:.x^{\circ}=180-63 = 117^{\circ}\ \ \text{(180° in straight line)}`

Special Properties, SMB-030

A regular decagon is pictured below.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the size of an internal angle of a decagon? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

i. `36^@`

ii. `144^@`

Show Worked Solution

i. `text{Sum of exterior angles = 360°}`

`text{Since the decagon is regular, all external angles are equal.}`

`:.x^{\circ}= 360/10 = 36^{\circ}`

ii. `text{Method 1: Using exterior angle}`

`text{Internal angle}`	`=180-\text{exterior angle}`
	`=180-36`
	`=144^{\circ}`

`text{Method 2: Using Internal angle sum formula}`

`text{Sum of internal angles}`	`=(n-2) xx 180`
	`=(10-2) xx 180`
	`=1440^{\circ}`

`:.\ text{Internal angle}\ = 1440/10 = 144^{\circ}`

Special Properties, SMB-029

A regular nonagon is pictured below.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`40^@`

Show Worked Solution

`text{Sum of exterior angles = 360°}`

`text{Since the nonagon is regular, all external angles are equal.}`

`:.x^{\circ}= 360/9 = 40^{\circ}`

Special Properties, SMB-028

A regular hexagon is pictured below.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`60^@`

Show Worked Solution

`text{Sum of exterior angles = 360°}`

`text{Since the hexagon is regular, all external angles are equal.}`

`:.x^{\circ}= 360/6 = 60^{\circ}`

Special Properties, SMB-027

A regular pentagon is pictured below.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`72^@`

Show Worked Solution

`text{Sum of exterior angles = 360°}`

`text{Since the pentagon is regular, all external angles are equal.}`

`:.x^{\circ}= 360/5 = 72^{\circ}`

Special Properties, SMB-024

A quadrilateral is drawn below.

What is the value of `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`117^@`

Show Worked Solution

`y^{\circ}=180-75 = 105^{\circ}\ \ \text{(180° in straight line)}`

`text{Sum of exterior angles = 360°}`

`z^{\circ}`	`=360-(130+105+62)`
	`=360-297`
	`=63^{\circ}`

`:.x^{\circ}=180-63 = 117^{\circ}\ \ \text{(180° in straight line)}`

Special Properties, SMB-023

A pentagon is drawn below.

What is the value of `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`99^@`

Show Worked Solution

`z^{\circ}=180-110 = 70^{\circ}\ \ \text{(180° in straight line)}`

`text{Sum of exterior angles = 360°}`

`y^{\circ}`	`=360-(72+82+70+55)`
	`=360-279`
	`=81^{\circ}`

`:.x^{\circ}=180-81 = 99^{\circ}\ \ \text{(180° in straight line)}`

Special Properties, SMB-022

A quadrilateral is drawn below.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`103^@`

Show Worked Solution

`text{Sum of exterior angles = 360°}`

`x`	`=360-(105+95+57)`
	`=360-257`
	`=103^{\circ}`

Special Properties, SMB-021

A five sided polygon is drawn below.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`60^@`

Show Worked Solution

`text{Sum of exterior angles = 360°}`

`x`	`=360-(65+85+80+70)`
	`=360-300`
	`=60^{\circ}`

Congruency, SMB-016

Igor was designing a shield using 10 congruent (isosceles) triangles, as shown in the diagram below.

How many degrees in the angle marked `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`72^@`

Show Worked Solution

`text(Angles at centre of circle)\ = 360/10 = 36^@`

`text{Since triangles are isosceles:}`

`180`	`= 36 + 2x`
`2x`	`= 180-36`
	`= 144 `
`:. x`	`= 72^@`

Special Properties, SMB-020 MC

`AB` is the diameter of a circle, centre `O`.

There are 3 triangles drawn in the lower semi-circle and the angles at the centre are all equal to `x^@`.

The three triangles are best described as:

isosceles
scalene
right-angled
equilateral

Show Answers Only

`D`

Show Worked Solution

`3x=180^{\circ}\ \=>\ x=60^{\circ} `

`AO=OC=OD=OB\ \ text{(radii of circle)}`

`=>\ text{Since angles opposite equal sides of a triangle are}`

`text(equal, all triangle angles can be found to equal 60°.)`

`:.\ text(The three triangles are equilateral.)`

`=>D`

Special Properties, SMB-019

A regular pentagon, a square and an equilateral triangle meet at a point.

What is the size of the angle `x°`? (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

`102°`

Show Worked Solution

`text(Sum of internal angles of pentagon)`

`= (n-2) xx 180`

`= 3 xx 180`

`= 540^@`

`text(Internal angle in pentagon)`

`= 540/5`

`= 108^@`

`:. x`	`= 360-(108 + 90 + 60)`
	`= 102^@`

Special Properties, SMB-018

A six sided figure is drawn below.

What is the sum of the six interior angles? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`720^@`

Show Worked Solution

`\text{Method 1}`

`text(Reflex angle) = 360-90 = 270^@`

`:.\ text(Sum of interior angles)`

`= (270 xx 2) + (30 xx 2) + (60 xx 2)`

`= 720^@`

`\text{Method 2}`

`text{Sum of interior angles (formula)}`

`= (n-2) xx 180`

`=4 xx 180`

`= 720^@`

Special Properties, SMB-017

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`80°`

Show Worked Solution

`text{Sum of internal angles (formula)}`

`= (n-2) xx 180`

`= 3 xx 180`

`= 540^@`

`:. x`	`= 540-(100 + 130 + 120 + 110)`
	`= 80^@`

Special Properties, SMB-016

Two identical quadrilaterals fit together to make this regular pentagon.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`108^@`

Show Worked Solution

`text(Consider regular pentagon:)`

`text{Sum of internal angles (formula)}`

`= (n-2) xx 180`

`= 3 xx 180`

`= 540^@`

`:. x`	`= 540/5`
	`= 108^@`

TIP: Two quadrilaterals joining does not make the internal angle sum = 2 × 360°!

Special Properties, SMB-015

A star is drawn on the inside of a regular pentagon, as shown below.

What is the size of the angle marked `x`? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`36^@`

Show Worked Solution

`text(Consider the triangle)\ ABC\ \ text(in the pentagon:)`

STRATEGY: The internal angle sum is 3 × 180 = 540 (since 3 triangles can be drawn internally from one point).

`text(Total degrees in a pentagon)`

`= 3 xx 180`

`= 540^@`

`text{Internal angle}\ =540/5 = 108^@\ \ \text{(regular pentagon)}`

`DeltaABC\ text(is isosceles)`

`:. x + x + 108`	`= 180`
`2x`	`= 72`
`x`	`= 36^@`

Special Properties, SMB-014

The sum of the interior angles of a 6 sided polygon can be found by first dividing it into triangles from one vertex.

What is the sum of the interior angles of this polygon? (2 marks)

Show Answers Only

`720\ text(degrees)`

Show Worked Solution

`text{Since the polygon can be divided into 4 separate triangles:}`

`text(Sum of interior angles)`

`= 4 xx 180`

`= 720\ text(degrees)`

Special Properties, SMB-012

`ABCD` is a rhombus. `AC` is the same length as the rhombus sides.

What is the size of `/_ DCB?` (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`120^@`

Show Worked Solution

`Delta ADC and Delta ABC\ text{are equiangular triangles.}`

`/_ DCA = /_ ACB = 60°`

`:. /_ DCB`	`=60 xx 2`
	`=120°`

Special Properties, SMB-013 MC

Which statement is always true?

Scalene triangles have two angles that are equal.
All angles in a parallelogram are equal.
The opposite sides of a trapezium are equal in length.
The diagonals of a rhombus are perpendicular to each other.

Show Answers Only

`D`

Show Worked Solution

`text{Consider each option:}`

`A:\ \text{Isosceles (not scalene) have two equal angles.}`

`B:\ \text{Only opposite angles in a parallelogram are equal.}`

`C:\ \text{At least one pair of opposite sides of a trapezium are not equal.}`

`D:\ \text{Rhombuses have perpendicular diagonals.}`

`=>D`

Special Properties, SMB-011 MC

The diagonals of which shape below cross at right-angles?

Show Answers Only

\(A\)

Show Worked Solution

`text(A rhombus has diagonals that cross at right-angles.)`

\(\Rightarrow A \)

Special Properties, SMB-010 MC

Which of these are always equal in length?

the diagonals of a rhombus
the diagonals of a parallelogram
the opposite sides of a parallelogram
the opposite sides of a trapezium

Show Answers Only

`C`

Show Worked Solution

`text{Consider each option:}`

`A:\ \text{rhombus diagonals are perpendicular but not always equal}`

`B:\ \text{parallelogram diagonals not always equal (see below)}`

`C:\ \text{always true (see above)}`

`D:\ \text{at least 1 pair of opposite sides of a trapezium are not equal}`
\(\Rightarrow C\)

Special Properties, SMB-009 MC

`PQRS` is a parallelogram.

Which of these must be a property of `PQRS`?

Line `PS` is perpendicular to line `PQ`.
Line `PQ` is parallel to line `PS`.
Diagonals `PR` and `SQ` are perpendicular.
Line `PS` is parallel to line `QR`.

Show Answers Only

`D`

Show Worked Solution

`text{By elimination:}`

`A\ \text{and}\ B\ \text{clearly incorrect.}`

`C\ \text{true if all sides are equal (rhombus) but not true for all parallelograms.}`

`text(Line)\ PS\ text(must be parallel to line)\ QR.`

`=>D`

Special Properties, SMB-008

The sum of the internal angles of a polygon can be calculated by drawing triangles from any given vertex as shown below.

What is the size of the angle marked `x` in the diagram below? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`107°`

Show Worked Solution

`text{Since the quadrilateral was divided into two triangles}`

`=>\ \text{Sum of internal angles}\ = 2 xx 180 = 360^{\circ}`

`:. x`	`= 360-(103 + 88 + 62)`
	`= 360-253`
	`= 107°`

Special Properties, SMB-007 MC

A closed shape has two pairs of equal adjacent sides.

What is the shape?

rectangle
trapezium
kite
triangle

Show Answers Only

`C`

Show Worked Solution

`text(Kite.)`

`text{(Note that a rectangle has a pair of equal opposite sides)}`

`=>C`

Special Properties, SMB-006

Eloise makes a sketch of the playground at her school.

What is the size of angle `x°`? (2 marks)

Show Answers Only

`143^@`

Show Worked Solution

`text(Interior angles of a quadrilateral add up to)\ 360^@.`

`:. /_ x`	`= 360-(72 + 88 + 57)`
	`= 143^@`

Special Properties, SMB-005 MC

`A`, `B` and `C` are vertices on the cube below.

What is the best description of `DeltaABC`?

isosceles
equilateral
scalene
right-angled

Show Answers Only

`D`

Show Worked Solution

`AB != AC != BC`

`angleBCA = 90^@`

`DeltaABC\ text(is both right-angled and scalene)`

`:.\ text(Right-angled is the BEST description)`

`=>D`

Special Properties, SMB-004 MC

Which one of the following triangles is impossible to draw?

a right angled triangle with two acute angles
an isosceles triangle with one right angle
a scalene triangle with three acute angles
a right angled triangle with one obtuse angle

Show Answers Only

`D`

Show Worked Solution

`text(A right angle = 90°.)`

`text{Since an obtuse angle is greater than 90°, it is impossible for}`

`text(a triangle, with an angle sum less than 180°, to have both.)`

`=>D`

Special Properties, SMB-003 MC

Select the statement that is true about triangle `ABC`.

Triangle `ABC` is a scalene triangle.
Triangle `ABC` has exactly 2 equal sides.
Triangle `ABC` is an equilateral triangle.
Triangle `ABC` is an obtuse triangle.

Show Answers Only

`C`

Show Worked Solution

`angleA = 180-(60 + 60) = 60^@`

`:. text(All angles are)\ 60^@.`

`:. text(Triangle)\ ABC\ text(is an equilateral.)`

`=>C`

Special Properties, SMB-002 MC

A triangle has two acute angles.

What type of angle couldn't the third angle be?

an acute angle
an obtuse angle
a right-angle
a reflex angle

Show Answers Only

`D`

Show Worked Solution

`text(A triangle’s angles add up to 180°, and a reflex angle is)`

`text(greater than 180°.)`

`:.\ text(The third angle cannot be reflex.)`

`=>D`

Special Properties, SMB-001 MC

Which of the following triangle types is impossible to draw?

a right-angled, scalene triangle
a right-angled, equilateral triangle
an obtuse-angled, isosceles triangle
an acute-angled, scalene triangle

Show Answers Only

`B`

Show Worked Solution

`text(An equilateral triangle has all angles = 60°.)`

`:.\ text(A right-angled, equilateral triangle is impossible.)`

`=>B`

Plane Geometry, 2UA 2004 HSC 2b

In the diagram, `ABC` is an isosceles triangle with `AB = AC` and `/_BAC = 38^@`. The line `BC` is produced to `D`.

Find the size of `/_ACD`. Give reasons for your answer. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`109^@`

Show Worked Solution

`/_ABC`	`= 1/2 (180-38)\ \ \ text{(base angle of isosceles}\ Delta ABC text{)}`
	`= 71^@`

`:.\ /_ACD`	`= 71 + 38\ \ \ text{(exterior angle of}\ Delta ABC text{)}`
	`= 109^@`

Plane Geometry, 2UA 2005 HSC 5b

The diagram shows a parallelogram `ABCD` with `∠DAB = 120^@`. The side `DC` is produced to `E` so that `AD = BE`.

Prove that `ΔBCE` is equilateral. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solutions)`

Show Worked Solution

`BC`	`= AD\ text{(opposite sides of parallelogram}\ ABCD)`
`∠BCD`	`= 120^@\ text{(opposite angles of parallelogram}\ ABCD)`
`∠BCE`	`= 60^@\ (∠DCE\ text{is a straight angle)}`
`∠CEB`	`= 60^@\ text{(base angles of isosceles}\ \Delta BCE)`
`∠CBE`	`= 60^@\ text{(angle sum of}\ ΔBCE)`

`:.ΔBCE\ text(is equilateral)`

Plane Geometry, 2UA 2008 HSC 4a

In the diagram, `XR` bisects `/_PRQ` and `XY\ text(||)\ QR`.

Prove that `Delta XYR` is an isosceles triangle. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ text{(See Worked Solutions)}`

Show Worked Solution

`text{Since}\ XR\ text{bisects}\ /_PRQ`

`/_XRQ`	`= /_YRX = theta`
`/_RXY`	`= theta\ \ \ text{(} text(alternate angles,)\ XY\ text(\|\|)\ QR text{)}`

`:.\ Delta XYR\ \ text(is isosceles)`

Plane Geometry, 2UA 2011 HSC 6a

The diagram shows a regular pentagon `ABCDE`. Sides `ED` and `BC` are produced to meet at `P`.

Find the size of `/_CDE`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Hence, show that `Delta EPC` is isosceles. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`108°`
`text(Proof)\ \ text{(see Worked Solutions)}`

Show Worked Solution

`text(Angle sum of pentagon)=(5-2) xx 180°=540°`

`:.\ /_CDE`	`= 540/5\ \ \ text{(regular pentagon has equal angles)}`
	`= 108°`

MARKER’S COMMENT: Very few students solved part (i) efficiently. Remember the general formula for the sum of internal angles equals (# sides – 2) x 90°.

ii. `text(Show)\ Delta EPC\ text(is isosceles)`

`text(S)text(ince)\ ED=CD\ \ text{(sides of a regular pentagon)}`

`Delta ECD\ text(is isosceles)`

`/_DEC=1/2 xx (180-108)= 36^{\circ}\ \ \ text{(Angle sum of}\ Delta DEC text{)}`

`/_CDP=72^@\ \ \ (\angle PDE\ \text{is a straight angle})`

`/_DCP=72^@\ \ \ (\angle PCB\ \text{is a straight angle})`

`=> /_CPD= 180-(72 + 72)=36^{\circ}\ \ \ text{(angle sum of}\ Delta CPD text{)}`

`:.\ Delta EPC\ \text(is isosceles)\ \ \ text{(2 equal angles)}`