Aussie Maths & Science Teachers: Save your time with SmarterEd
The network shows the distances, in kilometres, along a series of roads that connect towns.
What is the value of the largest weighted edge included in the minimum spanning tree for this network?
\(\text{Minimum spanning tree:}\)
\(\text{Using Kruskal’s algorithm:}\)
\(\text{Edge 1 = 4, Edge 2/3 = 4, Edge 4 = 6, Edge 5 = 9}\)
\(\therefore\ \text{The largest weighted edge in the MST = 9.}\)
\(\Rightarrow C\)
The vertices of the graph below represent cabins in a holiday park, and the water pump \((P)\) that will supply them. The numbers on the edges show the length, in metres, of water pipe required to connect the cabins and the pump.
The water pipes will cost $52 per metre.
Determine the minimum cost to link all the cabins to the water pump \((P)\). (3 marks)
--- 5 WORK AREA LINES (style=lined) ---
Minimum spanning tree:
\(\text{MST}\ =8+9+11+8+9+9+7+12=73\)
\(\therefore\ \text{Minimum cost}\ = 73 \times 52=\$3796\)
Eight houses in an estate are to be connected to the internet via underground cables.
The network below shows the possible connections between the houses.
The vertices represent the houses.
The numbers on the edges represent the length of cable connecting pairs of houses, in metres.
The graph that represents the minimum length of cable needed to connect all the houses is
The diagram shows a network with weighted edges. --- 0 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- a. \(\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC\ \text{to create}\) \(\text{a second MST (with equivalent weight = 24)}\) a. b. \(\text{Yes.}\) \(\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC\ \text{to create}\) \(\text{a second MST (with equivalent weight = 24)}\)
Show Answers Only
b. \(\text{Yes.}\)Show Worked Solution
♦ Mean mark (b) 45%.
A network of running tracks connects the points `A, B, C, D, E, F, G, H`, as shown. The number on each edge represents the time, in minutes, that a typical runner should take to run along each track. --- 4 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) ---
a. `text{Using Djikstra’s Algorithm:}` `=3+11+1+2+4+5+5` `=31` `text{Consider the MST below:}` `text{Total time (MST)}\ = 3+1+2+4+5+5+9=29` `:.\ text{Given tree is NOT a MST.}`
Show Worked Solution
`text{Shortest route}`
`=ABFGD`
`=3+1+5+5`
`=14`
b. `text{Total time of given spanning tree}`
♦ Mean mark (b) 47%.
The table below shows the distances, in kilometres, between a number of towns.
--- 0 WORK AREA LINES (style=lined) ---
a.
b. `text{Using Prim’s algorithm (starting at}\ Y):`
`text{1st edge:}\ YC`
`text{2nd edge:}\ CB`
`text{3rd edge:}\ SB`
`text{4th edge:}\ YM`
`text{Length of minimum spanning tree}`
`=275 + 150+60+530`
`=1015\ text{km}`
A network of roads connecting towns in an alpine region is shown below.
The distances between neighbouring towns, represented by vertices, are given in kilometres.
The region receives a large snowfall, leaving all roads between the towns closed to traffic.
To ensure each town is accessible by car from every other town, some roads will be cleared.
The minimal total length of road, in kilometres, that needs to be cleared is
`text{A partial minimal spanning tree can be drawn:}`
`text{Consider each option:}`
`A:\ text{If} \ x=50 \ text{(include),} \ y = 55 \ text{(include)}`
`-> \ text{Total length} = 251 + 50 + 55 != 361 \ text{(incorrect)}`
`B:\ text{If} \ x=50 \ text{(include),} \ y = 60 \ text{(include)}`
`-> \ text{Total length} = 251 + 50 + 55 = 356 \ text{(correct)}`
`text{Similarly, options} \ C, D, E \ text{can be shown to be incorrect.}`
`=> B`
The network diagram shows the travel times in minutes along roads connecting a number of different towns.
--- 8 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
a. `text{Using Prim’s algorithm (starting at}\ W):`
`text(1st edge:)\ \ WM`
`text(2nd edge:)\ \ WP`
`text(3rd/4th edges:)\ \ MU\ text(and)\ \ WF`
`text(5th edge:)\ \ MK`
`text(6th edge:)\ \ KQ`
`text(7th edge:)\ \ PC`
| b. | `text{Fastest route}\ (Q\ text(to)\ U)` | `= 45 + 20` |
| `= 65 \ text{minutes}` |
The network below shows the distances, in metres, between camp sites at a camping ground that has electricity.
The vertices `A` to `I` represent the camp sites.
The minimum length of cable required to connect all the camp sites is 53 m.
The value of `x`, in metres, is at least
The diagram represents a network with weighted edges.
--- 7 WORK AREA LINES (style=lined) ---
What is the length of the minimum spanning tree for this revised network? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
`text(One of many possibilities:)`
a. `text{Using Kruskal’s Algorithm (one of many possibilities):}`
`text{Edge 1 :}\ GH\ (1)`
`text{Edge 2 :}\ FH\ (2)`
`text{Edge 3 :}\ CF\ (2)`
`text{Edge 4 :}\ FD\ (2)`
`text{Edge 5 :}\ DE\ (2)`
`text{Edge 6 :}\ BC\ (3)`
`text{Edge 7 :}\ AB\ (2)`
| `text{Minimum length of spanning tree}` | `= 1 + 2 + 2 + 2 +2 + 3 +2` |
| `= 14` |
b. `text{Add}\ CK \ text{to the minimum spanning tree in (a).}`
| `therefore \ text(Revised length)` | `= 14 + 10` |
| `= 24` |
The following diagram shows the distances, in metres, along a series of cables connecting a main server to seven points, `A` to `G`, in a computer network.
Calculate the minimum length of cable, in metres, required to ensure that each of the seven points is connected to the main server directly or via another point. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
`text(Using Prim’s Algorithm:)`
`text{Edge 1: main server to D (15)}`
`text{Edge 2: DE (28)}`
`text{Edge 3: EG (30)}`
`text{Edge 4: GF (32)}`
`text{Edge 5: EA (35)}`
`text{Edge 6: AB (28)}`
`text{Edge 7: GC (35)}`
`:.\ text(Minimum length)`
`= 15 + 28 + 30 + 32 + 35 + 28 + 35`
`= 203\ text(m)`
The network diagram shows the tracks connecting 8 picnic sites in a nature park. The vertices `A` to `H` represents the picnic sites. The weights on the edges represent the distance along the tracks between the picnic sites, in kilometres.
Draw a minimum spanning tree and calculate the minimum length of water pipes required to supply water to all the sites if the water pipes can only be laid along the tracks. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
a. `text(One strategy – using Prim’s algorithm:)`
`text(Starting at)\ A`
`text(1st edge -)\ AB,\ \ text(2nd edge -)\ BC`
`text(3rd edge -)\ CH,\ \ text(4th edge -)\ HG`
`text(5th edge -)\ GF,\ \ text(6th edge -)\ HD`
`text(7th edge -)\ DE\ text(or)\ HE`
`text(Maximum length = 4 + 5 + 3 + 2 + 1 + 5 + 5 = 25 km)`
b. `text(Shortest Path is)\ CGHE`
An amusement park has five toilet areas, `A`, `B`, `C`, `D` and `E`, which are connected by pathways.
The table shows the length of some of the pathways, in metres.
The following network diagram is drawn to represent this information and a correct minimum spanning tree is shown by the solid lines.
Complete the network diagram including a possible value for each of the two edges `AC` and `BE`, and justify why `AC` and `BE` were not included as part of the minimum spanning tree. (3 marks)
--- 4 WORK AREA LINES (style=lined) ---
`BE > 500, AC > 450`
`text(Consider Kruskal’s algorithm for the given minimum spanning tree:)`
`CB ->\ text{1st edge (200 – minimum weight)}`
`BD ->\ text{2nd edge (300)}`
`AD ->\ text{3rd edge (450)}`
`=> AC=460\ \ text{(choose any value such that}\ \ AC>450)`
`DE ->\ text{4th edge (500)}`
`=> BE=510\ \ text{(choose any value such that}\ \ BE>500)`
`:. BE > 500\ (BE\ text(must be greater than)\ DE)`
`:. AC > 450\ (AC\ text(must be greater than)\ AD)`
This diagram shows the possible paths (in km) for laying gas pipes between various locations.
Gas is be supplied from one location. Any one of the locations can be the source of the supply.
What is the minimum total length of the pipes required to provide gas to all the locations?
`text(Using Kruskul’s Theorem:)`
`=>\ text(5 vertices – 4 edges needed)`
`text{Edge 1: The Hill → Carnie (9)}`
`text{Edge 2: Carnie → Bally (10)}`
`text{Edge 3: Bally → Eden (13)}`
`text{Edge 4: Carnie → Shallow End (14)}`
| `:.\ text(Maximum length)` | `= 9 + 10 + 13 + 14` |
| `= 46\ text(km)` |
`=>\ text(A)`
A weighted network diagram is shown below.
What is the weight of the minimum spanning tree?
`text(One Strategy – Using Kruskal’s Algorithm:)`
`text(There are 5 vertices, so we need 4 edges.)`
| `:.\ text(Weight)` | `= 4 + 4 + 5 + 6` |
| `= 19` |
`=>\ text(B)`
In a separate diagram or on the diagram above, show the minimum spanning tree . (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
`text(One strategy – Using Kruskal’s algorithm:)`
`text(Edges 1 – 5: AB, BC, DG, DH and EI)`
`text(Edges 6 – 8: CD, EF and HI)`
`(text(note AC cannot be chosen → creates a cycle))`
`text(NB: There is more than one minimal spanning tree in this)`
`text{circuit (having a weight of 19).}`
Highlight the minimal spanning tree of this network on the diagram above, or in a separate diagram. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
`text(One Strategy – Using Prim’s algorithm:)`
`text(6 vertices → 5 edges on spanning tree)`
`text(Starting at vertex A)`
`text(Edge 1: AC)`
`text(Edge 2: AD)`
`text{Edge 3: ED (reject CD which creates a cycle)}`
`text(Edge 4: EF)`
`text(Edge 5: BF)`
How many spanning trees are possible for this network?
| A. | `3` |
| B. | `8` |
| C. | `14` |
| D. | `30` |
`text(S)text(ince there are 6 vertices, each spanning tree will have)`
`text{5 edges (with no cycles).}`
`text(Consider if A and B are not connected, possible spanning)`
`text(trees are:)`
`text(3 other spanning trees exist when BF is not connected, and likewise)`
`text(when EF and ED are not connected.)`
`text(Finally, 2 other spanning trees exist when AD and AC are removed, and)`
`text(when AD and CD are removed.)`
| `:.\ text(Total spanning trees)` | `= 4 xx 3 + 2` |
| `= 14` |
Complete the minimal spanning tree of the network above on the diagram below. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
`text(One Strategy: Using Prim’s algorithm)`
`text(6 vertices → need 5 edges.)`
`text{Starting at vertex A (any vertex can be chosen)}`
`text(1st Edge: AB)`
`text{2nd Edge: AC (BF also possible)}`
`text(3rd Edge: CD)`
`text(4th Edge: BF)`
`text(5th Edge: AS)`
The diagram below is a connected network.
Complete the diagram below to show the minimal spanning tree of this network. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
`text(or)`
`text(One Strategy – Kruskul’s algorithm)`
`text(There are 6 vertices, so we need 5 edges.)`
`text{Edge 1: BC (least weight) – could have chosen ED}`
`text{Edge 2: DE (next least weight)}`
`text{Edge 3: AF (could have been CD)}`
`text(Edge 4: CD)`
`text{Edge 5: CF or EF (reject CE as it creates a cycle)}`
`text(or)`
A school is designing a computer network between five key areas within the school.
The cost of connecting the rooms is shown in the diagram below.
--- 0 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
a. `text(One Strategy: Using Prim’s Algorithm)`
`text(Starting vertex – Staff Room)`
`text(1st edge: Staff Room – Library)`
`text(2nd edge: Library – School Office)`
`text(3rd edge: Staff Room – IT Staff)`
`text(4th edge: Library – Computer Room)`
| b. | `text(Minimum Cost)` | `= 300 + 300 + 400 + 500` |
| `= $1500` |
This diagram shows the possible paths (in km) for laying gas pipes between various locations.
Gas is to be supplied from one location. Any one of the locations can be the source of the supply.
What is the minimum total length of the pipes required to provide gas to all the locations?
| A. | 32 km |
| B. | 34 km |
| C. | 36 km |
| D. | 38 km |
`text(Using Kruskal’s Algorithm:)`
`text(1st edge: Parkview – Summerville)\ (5)`
`text(2nd edge: Summerville – Newville)\ (8)`
`text(3rd edge: Beachview – Summerville)\ (10)`
`text(4th edge: Old Town – Newville)\ (11)`
`:.\ text(Minimum length of pipes.)`
`= 5 + 8 + 10 + 11`
`= 34`
`=> B`
Water will be pumped from a dam to eight locations on a farm.
The pump and the eight locations (including the house) are shown as vertices in the network diagram below.
The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
--- 1 WORK AREA LINES (style=lined) ---
The total length of all edges in the network is 1180 metres.
The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.
This minimum length of pipe is laid along some of the edges in the network.
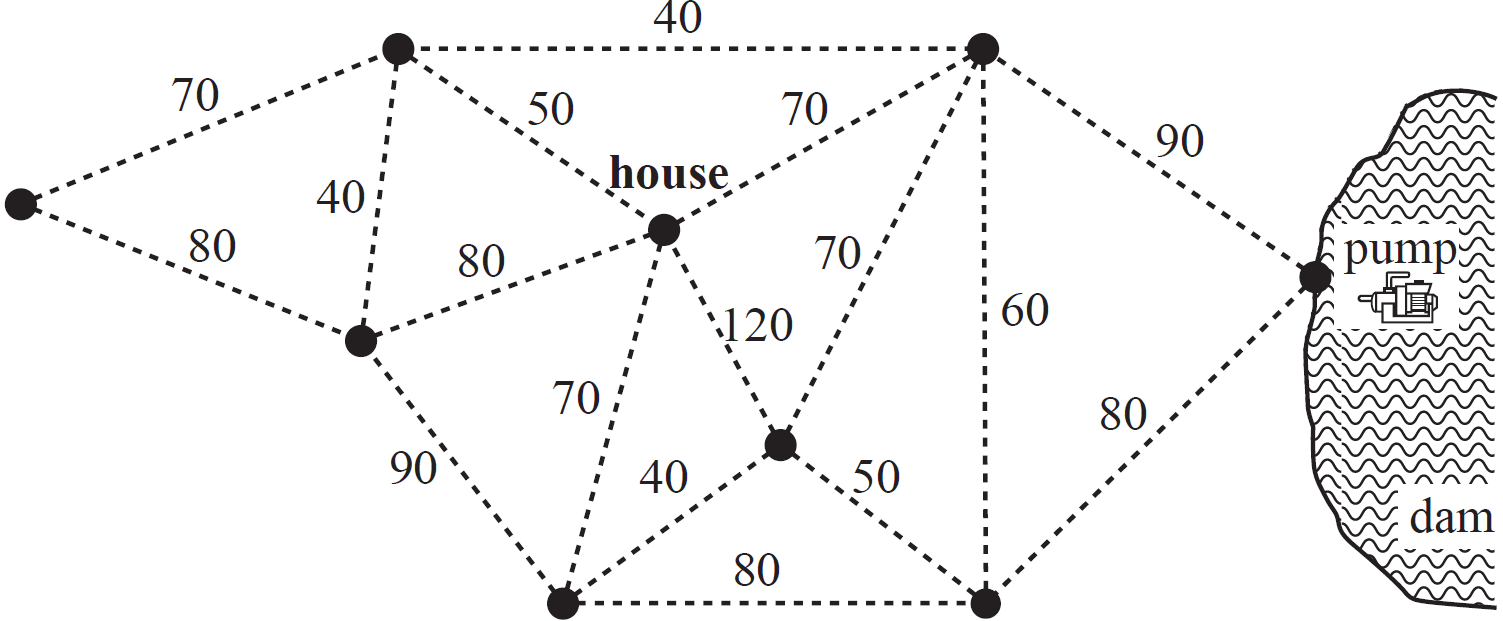
--- 1 WORK AREA LINES (style=lined) ---
a. `2\ text{(the house and the top right vertex)}`
b. `text(One Strategy – Using Prim’s algorithm:)`
`text(Starting at the house)`
`text(1st edge: 50)`
`text{2nd edge: 40 (either)}`
`text(3rd edge: 40)`
`text(4th edge: 60 etc…)`
c. `text(Minimum spanning tree)`
A new housing estate is being developed.
There are five houses under construction in one location.
These houses are numbered as points 1 to 5 below.
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.
--- 1 WORK AREA LINES (style=lined) ---
--- 0 WORK AREA LINES (style=lined) ---
a. `text(Minimum number of edges = 4)`
b. `text(One of many possibilities,)`
The minimum spanning tree for the network below includes the edge with weight labelled `k`.
The total weight of all edges for the minimum spanning tree is 33.
The value of `k` is
`text(Include)\ k\ text(as a given edge before using Kruskal’s Algorithm,)`
`text(Edge 1:)\ k`
`text(Edge 2: 1)`
`text(Edges 3-4: 2)`
`text(Edge 4: 3 etc…)`
`:.\ text(Minimum spanning tree)`
| `text(Total weight)` | `= k + 1+2+2+3+4+5+5+6` |
| `33` | `= k + 28` |
| `:. k` | `= 5` |
`=> D`
While on holiday, four friends visit a theme park where there are nine rides.
On the graph below, the positions of the rides are indicated by the vertices.
The numbers on the edges represent the distances, in metres, between rides.
Electrical cables are required to power the rides.
These cables will form a connected graph.
The shortest total length of cable will be used.
--- 1 WORK AREA LINES (style=lined) ---
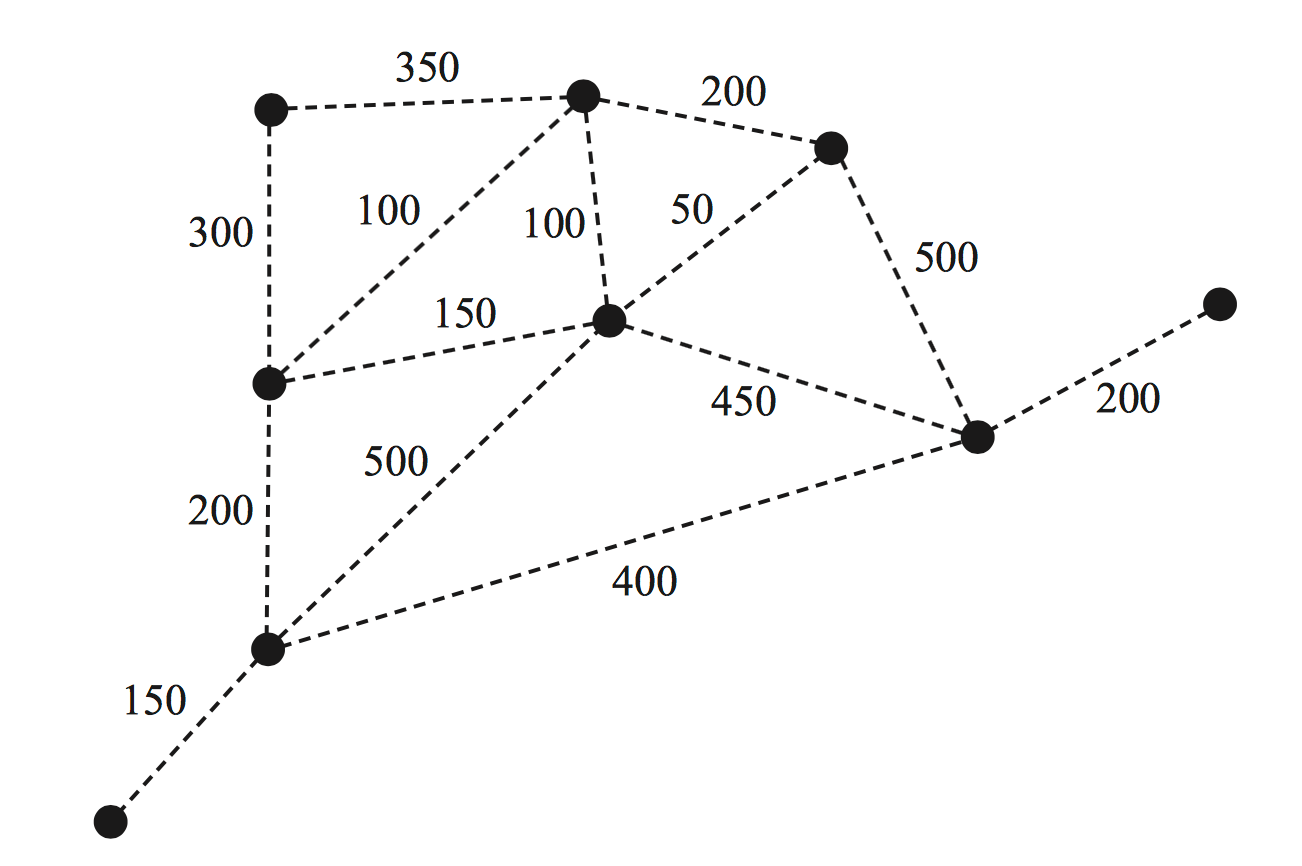
--- 0 WORK AREA LINES (style=lined) ---
a. `text{Minimum spanning tree}`
b.
a. `text{Minimum spanning tree.}`
b. `text(Using Kruskal’s Algorithm)`
`text(Edge 1: 50)`
`text(Edges 2–3: 100)`
`text{Edge 4: 150 (ignore the 150 edge that creates a circuit)}`
`text{Edges 5–6: 200 (ignore the 200 edge that creates a circuit)} `
`text(Edge 7: 300)`
`text(Edge 8: 400)`
A factory requires seven computer servers to communicate with each other through a connected network of cables.
The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
The edges on the graph represent the cables that could connect adjacent computer servers.
The numbers on the edges show the cost, in dollars, of installing each cable.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?
A copy of the graph above is provided below to assist with your working. (1 mark)
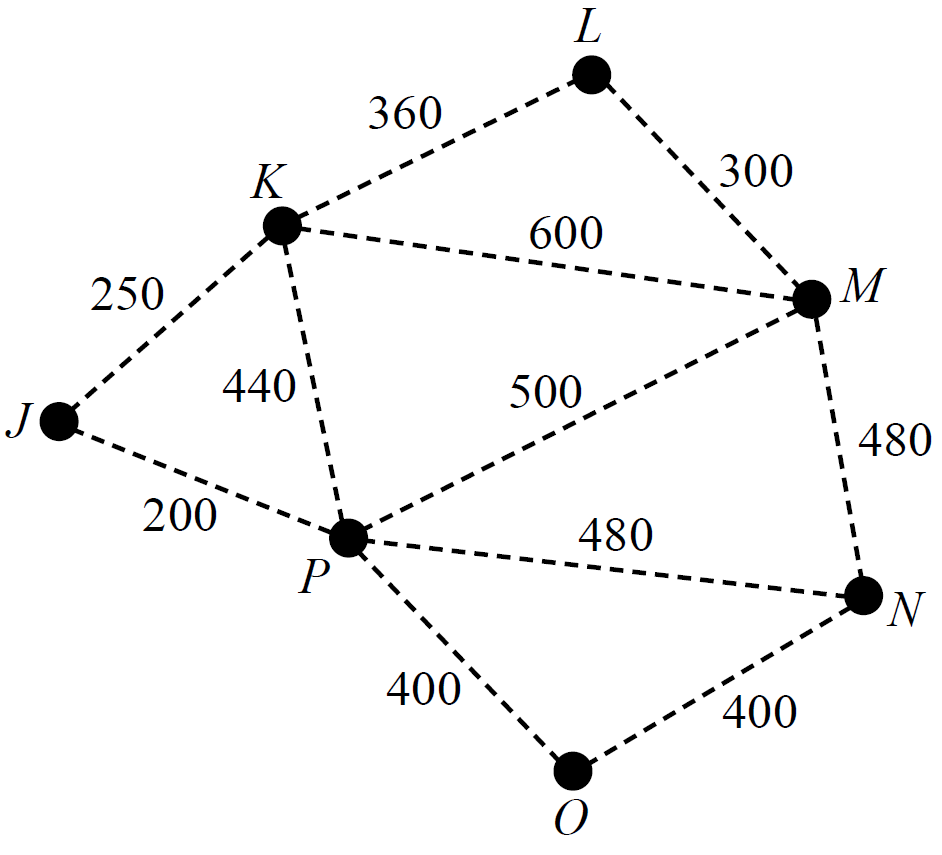
--- 0 WORK AREA LINES (style=lined) ---
a. `$300`
b. `text(Minimum cost of)\ K\ text(to)\ N`
`= 440 + 480`
`= $920`
c.i. `text(Using Prim’s Algorithm:)`
`text(Starting at Vertex)\ L`
`text{1st Edge: L → M (300)}`
`text{2nd Edge: L → K (360)}`
`text{3rd Edge: K → J (250)}`
`text{4th Edge: J → P (200) etc…}`
c.ii. `text(Disconnect)\ J – P\ text(and)\ O – P`
`text(Savings) = 200 + 400 = $600`
`text(Add in)\ M – N`
`text(C)text(ost) = $480`
| `:.\ text(Net savings)` | `= 600 – 480` |
| `= $120` |
At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
All locations are to be connected using the smallest total length of water pipe possible.
--- 1 WORK AREA LINES (style=lined) ---
a. `text(Using Prim’s Algorithm)`
`text(Starting at bottom right vertex)`
`text{1st Edge: 50}`
`text{2nd Edge: 40`
`text(3rd Edge: 50)`
`text(4th Edge: 40 etc…)`
b. `text(Total length of water pipe)`
`= 50+40+50+40+50+60+40+60+60+60`
`= 510\ text(metres)`
James, Dante, Tahlia and Chanel are four children playing a game.
In this children’s game, seven posts are placed in the ground.
The network below shows distances, in metres, between the seven posts.
The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.
This will be a minimal spanning tree.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
a. `text(Using Kruskal’s Algorithm)`
`text{Edges 1-3: 2}`
`text{Edges 4-5: 3 (2 edges with weight 3 create a circuit and are ignored)`
`text(Edge 6: 4)`
`text(or)`
b. `text(Length of minimal spanning tree)`
`= 2+2+2+3+3+4`
`= 16\ text(metres)`
c. `2`
The minimal spanning tree for the network below includes two edges with weightings `x` and `y.`
The length of the minimal spanning tree is 19.
The values of `x` and `y` could be
A. `x = 1 and y = 7`
B. `x = 2 and y = 5`
C. `x = 3 and y = 5`
D. `x = 4 and y = 5`
`text{Using Kruskal’s Algorithm (as a guide),}`
`text(Minimum spanning tree must be:)`
| `:. 19` | `= y + 3 + x + 2 + 1 + 5` |
| `8` | `= x + y` |
`=> C`
The minimal spanning tree for the network above will include the edge that has a weight of
A. `3`
B. `6`
C. `8`
D. `9`
`text(Using Kruskal’s Algorithm:)`
`text{Edge 1: 1 (minimum weight)}`
`text(Edge 2: 2)`
`text{Edge 3: 4 (edge weight 3 creates a circuit and is ignored)}`
`text(Edge 4: 5 etc…)`
`:.\ text(Minimum spanning tree is:)`
`rArr D`
The vertices of the graph above represent nine computers in a building. The computers are to be connected with optical fibre cables, which are represented by edges. The numbers on the edges show the costs, in hundreds of dollars, of linking these computers with optical fibre cables.
Based on the same set of vertices and edges, which one of the following graphs shows the cable layout (in bold) that would link all the computers with optical fibre cables for the minimum cost?
For the network above, the length of the minimal spanning tree is
A. `30`
B. `31`
C. `35`
D. `39`
`text(Using Kruskal’s algorithm:)`
`text{Edge 1: 2 (least weight)}`
`text(Edge 2: 3)`
`text(Edge 3: 4)`
`text(Edges 4-5: 5)`
`text{Edges 6-7: 8 (unused edges with weights <8 create circuits and are ignored)}`
`:.\ text(Minimal spanning tree)`
`= 2+3+4+5+5+8+8`
`= 35`
`=> C`
